If you are searching for the article which gives the proof by the equal intercepts theorem, then, it is the right page you are on. For Grade9 students, the equal intercepts concept feels difficult to learn. But, 9th Grade Math students can get clear knowledge by referring to these articles and which makes them feel easier.
In an equal intercept theorem, a transversal makes equal intercepts on three or more lines than any other transversal cutting them will also make an equal intercept. In this article, students get a step-by-step procedure of proof by the equal intercepts theorem.
What is meant by Intercepts in Maths?
Line segments are the intercepts made by the transversals by the lines L1 and L2. For example, in the below figure, AB is a transversal cutting the lines L and M at P and Q respectively. The line segment PQ is called the intercept made on the transversal AB by the lines L and M.
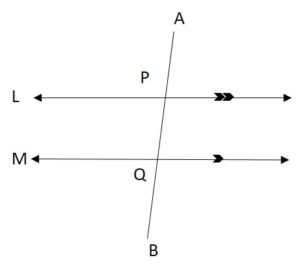
What is Equal Intercept in Maths?
In mathematics, the definition of equal intercepts is if a transversal creates equal intercepts on three or more parallel lines, then any other line cutting them will also make equal intercepts.
Equal Intercept Formula
The formula to find the equation of a line by intercept form is
\(\frac{x}{a}\) + \(\frac{y}{b}\) = 1
where a is x-intercept and b is y-intercept.
But given that the x & y-intercepts are equal.
Therefore, a = b
Thus, the equation of a line is
\(\frac{x}{a}\) + \(\frac{y}{a}\) = 1 ( As b= a)
x + y = a
⇒ x+ y- a= 0.
Example: Find the equation of a line that cuts off the equal intercepts on the axes and passes through the point (4, 6).
Solution:
As we know, the equation of a line is x+ y- a= 0
Now, find the value of a line that passes through the point (4,6)
Substituting, the given points in the equation of a line
i.e., x=4, y=6
4+6-a= 0
⇒ 10-a= 0
⇒ a= 10.
So, the equation of a line becomes
x+ y- 10= 0 (as a= 10)
Thus, x+ y- 10= 0 is the equation of a line that cuts off the equal intercepts on the coordinate axes.
Also Check:
Equal Intercepts Theorem Statement & Proof
Prove that in the given triangle ABC, and, D, E are the midpoints of AB and AC respectively. Prove that DE bisects AC.
Given In ∆ABC, AD = DB and DE ∥ BC.
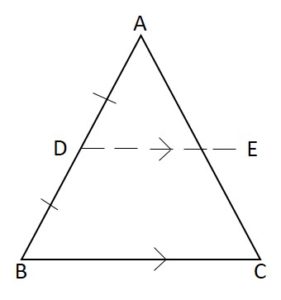
To Prove:
From ∆ABC, we have to prove that AE = EC.
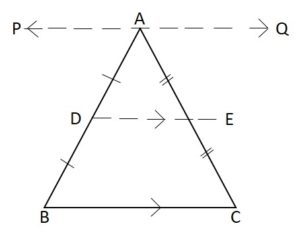
Construction:
Draw a line PQ through vertex A such that PQ ∥ BC.
Proof and Derivation
In ∆ABC, PQ, DE, and BC are three parallel lines i.e., PQ ∥ DE ∥ BC, and AB is a transversal that makes equal intercepts. i.e., AD = DB (given)
Since by equal intercept theorem we know if a transversal makes equal intercepts with three or more parallel lines, then any other transversal will also make equal intercepts.
Therefore, AE = EC and AC make equal intercepts. Hence, the statement is proved.
FAQ’s on Equal Intercepts Theorem
1. What is the intercept theorem and who invented the intercept theorem in mathematics?
The intercept theorem is also comprehended as Thales’s theorem and it has been invented by the ancient Babylonians and Egyptians, but firstly the known proof is found in Euclid’s Elements. of equalities. Q. E. D.
2. How do you find the equation of a line with equal intercepts?
The equation of a line that cuts off equal intercepts on the coordinate axes is \(\frac{x}{a}\) + \(\frac{y}{b}\) = 1. Thus, the equation of a line is x+ y- a= 0.
3. Which cuts off the equal intercepts and what is the slope of the line that cuts off equal intercepts on the coordinate axis?
The line cuts off the equal intercepts on the coordinate axis and the slope of the line is -1 when an equal intercept is on the axes.
