Students can use the Spectrum Math Grade 8 Answer Key Chapter 4 Lesson 4.5 Calculating Rate of Change in Functions as a quick guide to resolve any of their doubts.
Spectrum Math Grade 8 Chapter 4 Lesson 4.5 Calculating Rate of Change in Functions Answers Key
The rate of change that exists in a function can be calculated by finding the ratio of the amount of change in the output variable to the amount of change in the input variable.
![]()
Function tables can be used to find this rate of change.
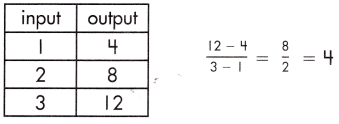
The rate of change for this function table is 4.
Find the rate of change for each function table. Write fractions in simplest form.
Question 1.
a.

_______
Answer:
2
Explanation:
The rate of change that exists in a function can be calculated by finding the ratio of the amount of change in the output variable to the amount of change in the input variable.
![]()
\(\frac{19 – 3}{10 – 2}\)
= \(\frac{16}{8}\) = 2
b.
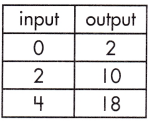
_______
Answer:
4
Explanation:
The rate of change that exists in a function can be calculated by finding the ratio of the amount of change in the output variable to the amount of change in the input variable.
![]()
\(\frac{18 – 2}{4 – 0}\)
= \(\frac{16}{4}\) = 4
c.
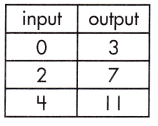
_______
Answer:
2
Explanation:
The rate of change that exists in a function can be calculated by finding the ratio of the amount of change in the output variable to the amount of change in the input variable.
![]()
\(\frac{11 – 3}{4 – 0}\)
= \(\frac{8}{4}\) = 2
Question 2.
a.
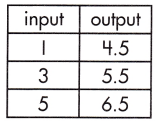
_______
Answer:
\(\frac{1}{2}\)
Explanation:
The rate of change that exists in a function can be calculated by finding the ratio of the amount of change in the output variable to the amount of change in the input variable.
![]()
\(\frac{6.5 – 4.5}{5 – 1}\)
= \(\frac{2}{4}\)
= \(\frac{1}{2}\)
b.
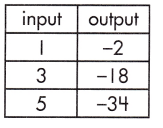
_______
Answer:
-8
Explanation:
The rate of change that exists in a function can be calculated by finding the ratio of the amount of change in the output variable to the amount of change in the input variable.
![]()
\(\frac{-34 – (-2)}{5 – 1}\)
= \(\frac{-32}{4}\) =-8
c.

_______
Answer:
-15
Explanation:
The rate of change that exists in a function can be calculated by finding the ratio of the amount of change in the output variable to the amount of change in the input variable.
![]()
\(\frac{-20 – 40}{5 – 1}\)
= \(\frac{-60}{4}\) = -15
Question 3.
a.
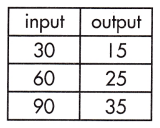
_______
Answer:
\(\frac{1}{3}\)
Explanation:
The rate of change that exists in a function can be calculated by finding the ratio of the amount of change in the output variable to the amount of change in the input variable.
![]()
\(\frac{35 – 15}{90 – 30}\)
= \(\frac{20}{60}\)
= \(\frac{1}{3}\)
b.
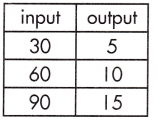
_______
Answer:
\(\frac{1}{6}\)
Explanation:
The rate of change that exists in a function can be calculated by finding the ratio of the amount of change in the output variable to the amount of change in the input variable.
![]()
\(\frac{15}{90}\) – \(\frac{5}{30}\)
= \(\frac{10}{60}\)
= \(\frac{1}{6}\)
c.
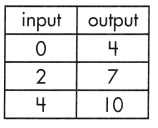
_______
Answer:
\(\frac{3}{2}\)
Explanation:
The rate of change that exists in a function can be calculated by finding the ratio of the amount of change in the output variable to the amount of change in the input variable.
![]()
\(\frac{10-4}{4-0}\)
= \(\frac{6}{4}\)
= \(\frac{3}{2}\)
Find the rate of change for each function table. Write fractions in simplest form.
Question 1.
a.
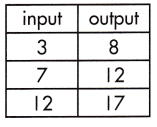
_______
Answer:
1
Explanation:
The rate of change that exists in a function can be calculated by finding the ratio of the amount of change in the output variable to the amount of change in the input variable.
![]()
\(\frac{17-8}{12-3}\)
= \(\frac{9}{9}\) = 1
b.
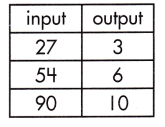
_______
Answer:
\(\frac{1}{9}\)
Explanation:
The rate of change that exists in a function can be calculated by finding the ratio of the amount of change in the output variable to the amount of change in the input variable.
![]()
\(\frac{10-3}{90-27}\)
= \(\frac{7}{63}\)
= \(\frac{1}{9}\)
c.
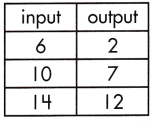
_______
Answer:
\(\frac{5}{4}\)
Explanation:
The rate of change that exists in a function can be calculated by finding the ratio of the amount of change in the output variable to the amount of change in the input variable.
![]()
\(\frac{12-2}{14-6}\)
= \(\frac{10}{8}\)
= \(\frac{5}{4}\)
Question 2.
a.
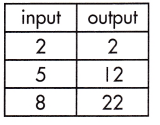
_______
Answer:
\(\frac{10}{3}\)
Explanation:
The rate of change that exists in a function can be calculated by finding the ratio of the amount of change in the output variable to the amount of change in the input variable.
![]()
\(\frac{22-2}{8-2}\)
= \(\frac{20}{6}\)
= \(\frac{10}{3}\)
b.

_______
Answer:
1
Explanation:
The rate of change that exists in a function can be calculated by finding the ratio of the amount of change in the output variable to the amount of change in the input variable.
![]()
\(\frac{23-14}{12-3}\)
= \(\frac{9}{9}\) = 1
c.
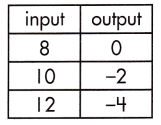
_______
Answer:
-1
Explanation:
The rate of change that exists in a function can be calculated by finding the ratio of the amount of change in the output variable to the amount of change in the input variable.
![]()
\(\frac{-4-0}{12-8}\)
= \(\frac{-4}{4}\) = -1
Question 3.
a.
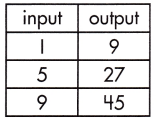
_______
Answer:
\(\frac{9}{2}\)
Explanation:
The rate of change that exists in a function can be calculated by finding the ratio of the amount of change in the output variable to the amount of change in the input variable.
![]()
\(\frac{45-9}{9-1}\)
= \(\frac{36}{8}\)
= \(\frac{9}{2}\)
b.
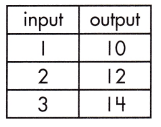
_______
Answer:
2
Explanation:
The rate of change that exists in a function can be calculated by finding the ratio of the amount of change in the output variable to the amount of change in the input variable.
![]()
\(\frac{14-10}{3-1}\)
= \(\frac{4}{2}\) = 2
c.
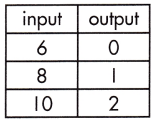
_______
Answer:
\(\frac{1}{2}\)
Explanation:
The rate of change that exists in a function can be calculated by finding the ratio of the amount of change in the output variable to the amount of change in the input variable.
![]()
\(\frac{2-0}{10-6}\)
= \(\frac{2}{4}\)
= \(\frac{1}{2}\)
Question 4.
a.
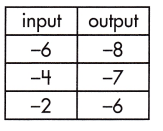
_______
Answer:
\(\frac{1}{2}\)
Explanation:
The rate of change that exists in a function can be calculated by finding the ratio of the amount of change in the output variable to the amount of change in the input variable.
![]()
\(\frac{-2-(-8)}{-6-6}\)
= \(\frac{6}{12}\)
= \(\frac{1}{2}\)
b.
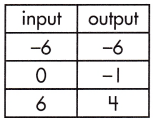
_______
Answer:
\(\frac{5}{6}\)
Explanation:
The rate of change that exists in a function can be calculated by finding the ratio of the amount of change in the output variable to the amount of change in the input variable.
![]()
\(\frac{4-(-6)}{6-(-6)}\)
= \(\frac{10}{12}\)
= \(\frac{5}{6}\)
c.
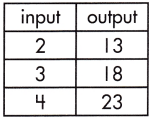
_______
Answer:
5
Explanation:
The rate of change that exists in a function can be calculated by finding the ratio of the amount of change in the output variable to the amount of change in the input variable.
![]()
\(\frac{23-13}{4-2}\)
= \(\frac{10}{2}\) = 5
Read More: