Today we are here with an article that helps you to know about the concept of Equal Intercepts Theorem. In geometry, intercepts are the lines that cross or make a transversal in two or more parallel lines. Here, 9th Grade Math students can learn and grasp the equal intercepts theorem statement and the proof in detail which gives a grip to solve the problems on equal intercepts.
What is Equal Intercept Theorem?
Equal intercepts are the concept of geometry where there are many theorems in geometry and it is one of them. The theorem proves, ” If a transversal forms equal intercepts on three or more parallel lines, any other line cutting them will also make equal intercepts “.
Consequently, the given three parallel lines, a line passing through them form intercepts in an equal ratio of the distance between the lines given. We can prove this theorem by any geometrical proof, let us study, how the theorem is proved?
Equal Intercepts Theorem Statement
The equal intercepts theorem says that ” If a transversal makes equal intercepts on three or more parallel lines then any other transversal cutting them will also make equal intercepts “.
Given The three straight lines l, m, and n such that l ∥ m ∥ n and PQ = QR.
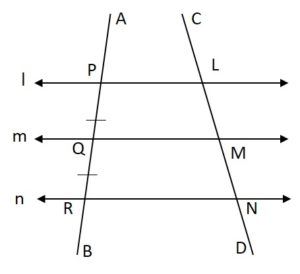
To Prove:
We have to prove that the lines LM = MN.
For that, we will construct the given above diagram.
Construction:
To prove the given statement, we draw a line from the point P to N and name the midpoint as ‘O’.
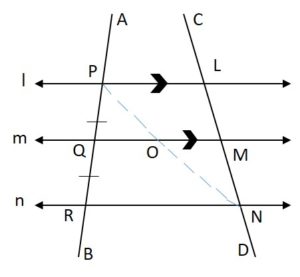
Proof of the Theorem:
From the construction, we have triangles ΔPRN and ΔPNL.
In triangle ΔPRN,
Q is the midpoint of PR (given) and QO ∥ RN
⇒ QO bisects PN (from the converse of the midpoint theorem)
In triangle ΔPNL,
O is the midpoint of PN (from construction) and OM ∥ PL
⇒ OM bisects LN (from the converse of the midpoint theorem)
Therefore, LM = MN.
Hence, the statement is proved.
Example:
In the given triangle ABC, DE ∥ BC, then find the value of EC?
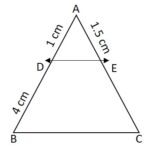
Solution:
From the given triangle ABC, DE ∥ BC.
According to the basic proportionality theorem, the line drawn parallel to one side divides the other side in an equal ratio.
Given AD =1cm, DB =4cm, and AE =1.5cm
Now, \(\frac{AD}{DB}\) = \(\frac{AE}{EC}\)
⇒ \(\frac{1}{4}\) = \(\frac{1.5}{EC}\)
⇒ EC = 1.5 × 4
⇒ EC = 6cm
Thus, the value of EC is 6cm.
See More:
FAQ’s on Equal Intercepts
1. What is the meaning of equal intercept?
If there are three or more parallel lines and the intercepts made by them on the transversal are equal then the equivalent intercepts on any other transversal are also equal.
2. What is the slope of equal intercept?
In the equal intercepts, from the given line cuts intercepts of equal lengths. Thus, the slope of an equal intercept form is ‘m=-1’.
3. Write two applications of the equal intercept theorem?
Two applications of equal intercept theorem are the basic proportionality theorem and the converse of the midpoint theorem.
4. How do you prove the equal intercept theorem?
If we have three or more parallel lines and the intercepts made by them on the transversal are equal and the corresponding intercepts on other transversals also make equal.
5. Are the equal intercepts formed by parallel lines only?
Yes, equal intercepts are done by parallel lines only, but intercepts can be formed by any line.
