Enhance your knowledge by practicing the problems from Go Math Grade 6 Answer Key Chapter 3 Understand Positive and Negative Numbers. You can get the free pdfs of Go Math Grade 6 Chapter 3 Understand Positive and Negative Numbers Solution Key. We have provided the Go Math Grade 6 Answer Key in pdf format so that you can practice online and offline mode. Take the given resources as references and score well in the exams.
Go Math Grade 6 Chapter 3 Understand Positive and Negative Numbers Answer Key
Improve your math skills with the help of Go Math 6th Standard Answer Key Chapter 3 Understand Positive and Negative Numbers. Unlimited practice with all the maths questions and answers along with the practice questions. It is mandatory to practice with the Grade 6 Chapter 3 Solution key to score maximum marks in the exams. Check out the links given the below sections before you start your preparation.
Lesson 1: Understand Positive and Negative Numbers
- Understand Positive and Negative Numbers – Page No. 141
- Understand Positive and Negative Numbers – Page No. 142
- Understand Positive and Negative Numbers – Page No. 143
- Understand Positive and Negative Numbers Lesson Check – Page No. 144
Lesson 2: Compare and Order Integers
- Compare and Order Integers – Page No. 147
- Compare and Order Integers – Page No. 148
- Compare and Order Integers – Page No. 149
- Compare and Order Integers Lesson Check – Page No. 150
Lesson 3: Rational Numbers and the Number Line
- Rational Numbers and the Number Line – Page No. 153
- Rational Numbers and the Number Line – Page No. 154
- Rational Numbers and the Number Line – Page No. 155
- Rational Numbers and the Number Line Lesson Check– Page No. 156
Lesson 4: Compare and Order Rational Numbers
- Compare and Order Rational Numbers – Page No. 159
- Compare and Order Rational Numbers – Page No. 160
- Compare and Order Rational Numbers – Page No. 161
- Compare and Order Rational Numbers Lesson Check – Page No. 162
Mid-Chapter Checkpoint
Lesson 5: Absolute Value
- Absolute Value – Page No. 167
- Absolute Value – Page No. 168
- Absolute Value – Page No. 169
- Absolute Value – Page No. 170
Lesson 6: Compare Absolute Values
- Compare Absolute Values – Page No. 173
- Compare Absolute Values – Page No. 174
- Compare Absolute Values – Page No. 175
- Compare Absolute Values – Page No. 176
Lesson 7: Rational Numbers and the Coordinate Plane
- Rational Numbers and the Coordinate Plane – Page No. 179
- Rational Numbers and the Coordinate Plane – Page No. 180
- Rational Numbers and the Coordinate Plane – Page No. 181
- Rational Numbers and the Coordinate Plane – Page No. 182
Lesson 8: Ordered Pair Relationships
- Ordered Pair Relationships – Page No. 185
- Ordered Pair Relationships – Page No. 186
- Ordered Pair Relationships – Page No. 187
- Ordered Pair Relationships – Page No. 188
Lesson 9: Distance on the Coordinate Plane
- Distance on the Coordinate Plane – Page No. 191
- Distance on the Coordinate Plane – Page No. 192
- Distance on the Coordinate Plane – Page No. 193
- Distance on the Coordinate Plane – Page No. 194
Lesson 10: Problem Solving • The Coordinate Plane
- The Coordinate Plane – Page No. 197
- The Coordinate Plane – Page No. 198
- The Coordinate Plane – Page No. 199
- The Coordinate Plane – Page No. 200
Chapter 3 Review/Test
- Review/Test – Page No. 201
- Review/Test – Page No. 202
- Review/Test – Page No. 203
- Review/Test – Page No. 204
- Review/Test – Page No. 205
- Review/Test – Page No. 206
Share and Show – Page No. 141
Graph the integer and its opposite on a number line.
Question 1.
−7
Type below:
__________
Answer:
7
Explanation:
The opposite number of -7 is 7
Question 2.
9
Type below:
__________
Answer:
-9
Explanation:
The opposite number of 9 is -9
Name the integer that represents the situation, and tell what 0 represents in that situation.
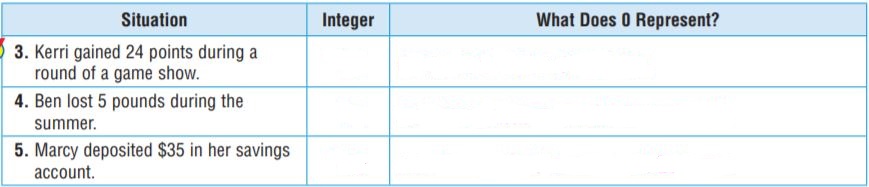
Question 3.
Type below:
__________
Answer:
Integer: 24
0 represents: neither gaining nor losing points
Explanation:
Kerri gained 24 pounds during a round of the game show. So, he has a positive integer.
Question 4.
Type below:
__________
Answer:
Integer: -5
0 represents: Ben neither gains nor loses during the summer
Explanation:
Ben lost 5 points during the summer. He has a negative integer.
Question 5.
Type below:
__________
Answer:
Integer: 35
0 represents: No changes in her savings account.
Explanation:
Marcy deposited $35 in her savings account. She has a positive integer.
On Your Own
Write the opposite of the integer.
Question 6.
−98
Type below:
__________
Answer:
98
Explanation:
The integer −98 is on the left side of 0.
So, the opposite of -98 is 98
Question 7.
0
Type below:
__________
Answer:
0
Explanation:
Opposite of 0 is 0
Question 8.
−53
Type below:
__________
Answer:
53
Explanation:
The integer −53 is on the left side of 0.
So, the opposite of -53 is 53
Name the integer that represents the situation, and tell what 0 represents in that situation.
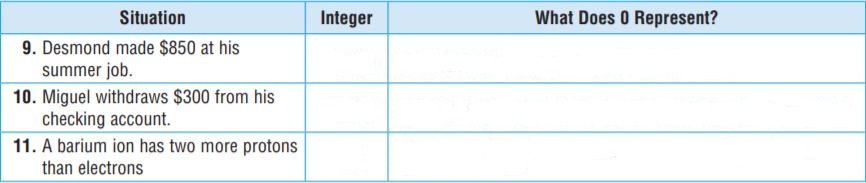
Question 9.
Type below:
__________
Answer:
Integer: $850
0 represents: Desmond neither gains nor loses at his summer job
Question 10.
Type below:
__________
Answer:
Integer: -300
0 represents: No change from his checking point
Question 11.
Type below:
__________
Answer:
Integer: 2
0 represents: No change of protons than electrons
Write the opposite of the opposite of the integer.
Question 12.
−23
Type below:
__________
Answer:
-23
Explanation:
The opposite integer of the -23 is 23
The opposite integer of the 23 is -23.
So, the opposite of the opposite of the integer -23 is -23.
Question 13.
17
Type below:
__________
Answer:
17
Explanation:
The opposite integer of the 17 is -17
The opposite integer of the -17 is 17.
So, the opposite of the opposite of the integer 17 is 17.
Question 14.
−125
Type below:
__________
Answer:
-125
Explanation:
The opposite integer of the -125 is 125
The opposite integer of the 125 is -125.
So, the opposite of the opposite of the integer -125 is -125.
Question 15.
Suppose you know a certain number’s distance from zero on the number line. Explain how you could find the number’s distance from its opposite.
Type below:
__________
Answer:
The distance between a number’s place on the number line and 0 is called the number’s [absolute value]. To write the absolute value of a number, use short vertical lines (|) on either side of the number. For example, the absolute value of −5 is written |−5|
Problem Solving + Applications – Page No. 142
Wind makes the air temperature seem colder. The chart gives the wind chill temperature (what the temperature seems like) at several air temperatures and wind speeds. Use the chart for 16–18.
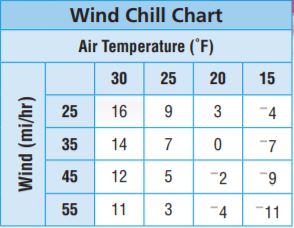
Question 16.
At 6 a.m., the air temperature was 20°F and the wind speed was 55 mi/hr. What was the wind chill temperature at 6 a.m.?
Type below:
__________
Answer:
At 6 a.m., the air temperature was 20°F and the wind speed was 55 mi/hr.
The winds chill temperature at 6 a.m. is -4
Question 17.
At noon, the air temperature was 15°F and the wind speed was 45 mi/hr. At what air temperature and wind speed would the wind chill temperature be the opposite of what it was at noon?
Type below:
__________
Answer:
If the air temperature was 15°F and the wind speed was 45 mi/hr, the wind chill temperature is -9. The opposite number of -9 is 9.
So, at the air temperature was 25°F and the wind speed was 25 mi/hr, the wind chill temperature is the opposite of what it was at noon.
Question 18.
The wind was blowing 35 mi/hr in both Ashton and Fenton. The wind chill temperatures in the two towns were opposites. If the air temperature in Ashton was 25°F, what was the air temperature in Fenton?
Type below:
__________
Answer:
The wind was blowing 35 mi/hr in both Ashton and Fenton.
If the air temperature in Ashton was 25°F, the wind chill temperature is 7.
The wind chill temperatures in the two towns were opposites.
So, the wind chill temperature in Fenton is -7. So, the air temperature in Fenton was 15°F.
Question 19.
Sense or Nonsense? Claudia states that the opposite of any integer is always a different number than the integer. Is Claudia’s statement sense or nonsense? Explain.
Type below:
__________
Answer:
Claudia is correct.
Because the opposite of any integer is always a different number than the integer.
Example: The opposite of 7 is -7.
Question 20.
For numbers 20a−20d, choose Yes or No to indicate whether the situation can be represented by a negative number.
20a. Death Valley is located 282 feet below sea level.
20b. Austin’s golf score was 3 strokes below par.
20c. The average temperature in Santa Monica in August is 75°F.
20d. Janai withdraws $20 from her bank account.
20a. __________
20b. __________
20c. __________
20d. __________
Answer:
20a. Yes
20b. Yes
20c. No
20d. Yes
Understand Positive and Negative Numbers – Page No. 143
Graph the integer and its opposite on a number line.
Question 1.
−6
Type below:
__________
Answer:
6
![]()
Explanation:
The opposite number of -6 is 6
Question 2.
3
Type below:
__________
Answer:
-3
![]()
Explanation:
The opposite number of -3 is 3
Question 3.
10
Type below:
__________
Answer:
-10
![]()
Explanation:
The opposite number of 10 is -10
Question 4.
−8
Type below:
__________
Answer:
8
![]()
Explanation:
The opposite number of -8 is 8
Name the integer that represents the situation, and tell what 0 represents in that situation

Question 5.
Type below:
__________
Answer:
Integer: -60
0 represents: No changes in the account balance
Explanation:
Question 6.
Type below:
__________
Answer:
Integer: 12
0 represents: neither gaining nor losing points
Explanation:
Write the opposite of the opposite of the integer.
Question 7.
−20
Type below:
__________
Answer:
-20
Explanation:
The opposite integer of the -20 is 20
The opposite integer of the 20 is -20.
So, the opposite of the opposite of the integer -20 is -20
Question 8.
4
Type below:
__________
Answer:
4
Explanation:
The opposite integer of the 4 is -4
The opposite integer of the -4 is 4.
So, the opposite of the opposite of the integer -4 is 4.
Question 9.
95
Type below:
__________
Answer:
95
Explanation:
The opposite integer of the 95 is -95
The opposite integer of the -95 is 95.
So, the opposite of the opposite of the integer 95 is 95.
Question 10.
−63
Type below:
__________
Answer:
-63
Explanation:
The opposite integer of the -63 is 63
The opposite integer of the 63 is -63.
So, the opposite of the opposite of the integer -63 is -63.
Problem Solving
Question 11.
Dakshesh won a game by scoring 25 points. Randy scored the opposite number of points as Dakshesh. What is Randy’s score?
Type below:
__________
Answer:
Randy’s score -25.
Explanation:
Dakshesh won a game by scoring 25 points. Randy scored the opposite number of points as Dakshesh.
The opposite number of 25 is -25
Question 12.
When Dakshesh and Randy played the game again, Dakshesh scored the opposite of the opposite of his first score. What is his score?
Type below:
__________
Answer:
25 points
Explanation:
When Dakshesh and Randy played the game again, Dakshesh scored the opposite of the opposite of his first score.
The opposite of the 25 is -25.
The opposite of the -25 is 25.
The opposite of the opposite of his first score is 25
Question 13.
Give three examples of when negative numbers are used in daily life.
Type below:
__________
Answer:
1) negative numbers in weather reports and on food packaging. The temperature -5°C is ‘negative five degrees’ and it means 5 degrees below zero.
2) The floors as you go down in a lift, starting on the third floor you’ll see:
3, 2, 1, 0, -1, -2.
In this example building, -2 is the second floor underground
3) When you spend more money than you have in your bank account it shows up as a negative number.
Lesson Check – Page No. 144
Name the integers that represent each situation.
Question 1.
During their first round of golf, Imani was 7 strokes over par and Peter was 8 strokes below par.
Type below:
__________
Answer:
In the first round of golf, Imani has scored 7 strokes over par. So, it is represented by 7.
Peter was scored 8 strokes below par. So, it is represented by -8.
Therefore, the answer is 7 and -8.
Question 2.
Wyatt earned $15 baby-sitting on Saturday. Wilson spent $12 at the movies.
Type below:
__________
Answer:
He has $3 dollars left because you take 12 from 15 and you get 3
$15 – $12 = $3
Spiral Review
Question 3.
Mr. Nolan’s code for his ATM card is a 4-digit number. The digits of the code are the prime factors of 84 listed from least to greatest. What is the code for Mr. Nolan’s ATM card?
Type below:
__________
Answer:
2237
Explanation:
Mr.Nolan’s code for his ATM card is a 4- digit number.
The digits of the code are the prime factors of 84 listed from least to greatest.
In order to find the code, we have to find the prime factors of 84.
The prime factors of 84 are 2,2,3 and 7.
Therefore, the code=2237
Question 4.
Over a four-year period, a tree grew 2.62 feet. If the tree grows at a constant rate, how many feet did the tree grow each year?
Type below:
__________
Answer:
0.655 feet
Explanation:
Each year the tree grows
( 2.62 ÷ 4 ) feet
= 0.655 feet
Question 5.
Omarion has \(\frac{9}{10}\) of the pages in a book remaining to read for school. He reads \(\frac{2}{3}\) of the remaining pages over the weekend. What fraction of the book does Omarion read over the weekend?
Type below:
__________
Answer:
\(\frac{3}{5}\)
Explanation:
Omarion has 9/10 of pages in a book remaining to read for school and he reads 2/3 of the remaining pages over the weekend.
The fraction of the book trade over the weekend = the fraction of the pages read over the weekend multiplied by the fraction of the book that is remaining to be read.
Therefore, the fraction of the book that Omarion trad over the weekend is 2/3 × 9/10 = 3/5
Thus, the required fraction of the book that Omarion trad over the weekend is 3/5
Question 6.
Marianne has \(\frac{5}{8}\) pound of peas. She cooks \(\frac{2}{3}\) of those peas for 5 people. If each person is served an equal amount, how much peas did each person get?
Type below:
__________
Answer:
\(\frac{1}{12}\) pounds
Explanation:
Marianne has \(\frac{5}{8}\) pound of peas. IShe cooks \(\frac{2}{3}\) of those peas for 5 people.
Marianne cooks 5/8 × 2/3 = 5/12 pounds.
(5/12)/5 = 1/12 pounds
the answer is
Share and Show – Page No. 147
Compare the numbers. Write < or >.
Question 1.
–8 _____ 6
Answer:
–8 < 6
Explanation:
-8 is to the left of 6 on the number line.
So, -8 is less than 6.
Question 2.
1 _____ –8
Answer:
1 > –8
Explanation:
1 is to the right of -8 on the number line.
So, 1 is greater than -8.
Question 3.
–4 _____ 0
Answer:
-4 < 0
Explanation:
-4 is to the left of 0 on the number line.
So, -4 is less than 0.
Question 4.
3 _____ –7
Answer:
3 > -7
Explanation:
3 is to the right of -7 on the number line.
So, 3 is greater than -7.
Order the numbers from least to greatest.
Question 5.
4, –3, –7
Type below:
__________
Answer:
-7, -3, 4
Explanation:
-7 is to the left of -3 on the number line. -3 is to the left of 4 on the number line.
So, -7 < -3 < 4
Question 6.
0, –1, 3
Type below:
__________
Answer:
-1, 0, 3
Explanation:
-1 is to the left of 0 on the number line. 0 is to the left of 3 on the number line.
So, -1 < 0 < 3
Question 7.
–5, –3, –9
Type below:
__________
Answer:
-9, -5, -3
Explanation:
-9 is to the left of -5 on the number line. -5 is to the left of -3 on the number line.
So, -9 < -5 < -3
Order the numbers from greatest to least.
Question 8.
–1, –4, 2
Type below:
__________
Answer:
2, -1, -4
Explanation:
2 is to the right of -1 on the number line. -1 is to the right of -4 on the number line.
So, 2 > -1 > -4
Question 9.
5, 0, 10
Type below:
__________
Answer:
10, 5, 0
Explanation:
10 is to the right of 5 on the number line. 5 is to the right of 0 on the number line.
So, 10 > 5 > 0
Question 10.
–5, –4, –3
Type below:
__________
Answer:
-3, -4, -5
Explanation:
-3 is to the right of -4 on the number line. -4 is to the right of -5 on the number line.
So, -3 > -4 > -5
On Your Own
Order the numbers from least to greatest.
Question 11.
2, 1, –1
Type below:
__________
Answer:
-1, 1, 2
Explanation:
-1 is to the left of 1 on the number line. 1 is to the left of 2 on the number line.
So, -1 < 1 < 2
Question 12.
–6, –12, 30
Type below:
__________
Answer:
-12, -6, 30
Explanation:
-12 is to the left of -6 on the number line. -6 is to the left of 30 on the number line.
So, -12 < -6 < 30
Question 13.
15, –9, –20
Type below:
__________
Answer:
-20, -15, -9
Explanation:
-20 is to the left of -15 on the number line. -15 is to the left of -9 on the number line.
So, -20 < -15 < -9
Order the number from greatest to least.
Question 14.
–13, 14, –14
Type below:
__________
Answer:
14, -13, -14
Explanation:
14 is to the right of -13 on the number line. -13 is to the right of -14 on the number line.
So, 14 > -13 > -14
Question 15.
–20, –30, –40
Type below:
__________
Answer:
-20, -30, -40
Explanation:
-20 is to the right of -30 on the number line. -30 is to the right of -40 on the number line.
So, -20 > -30 > -40
Question 16.
9, –37, 0
Type below:
__________
Answer:
9, 0, -37
Explanation:
9 is to the right of 0 on the number line. 0 is to the right of -37 on the number line.
So, 9 > 0 > -37
Question 17.
Saturday’s low temperature was −6°F. Sunday’s low temperature was 3°F. Monday’s low temperature was −2°F. Tuesday’s low temperature was 5°F. Which day’s low temperature was closest to 0°F?
Type below:
__________
Answer:
Monday’s temperature was closest to 0°F
Explanation:
Saturday’s low temperature was −6°F. Sunday’s low temperature was 3°F. Monday’s low temperature was −2°F. Tuesday’s low temperature was 5°F.
-2 is closest to 0. So, Monday’s temperature was closest to 0°F.
Question 18.
Use Symbols Write a comparison using < or > to show that South America’s Valdes Peninsula (elevation −131 ft) is lower than Europe’s Caspian Sea (elevation −92 ft).
Type below:
__________
Answer:
South America’s Valdes Peninsula < Europe’s Caspian Sea
Explanation:
South America’s Valdes Peninsula (elevation −131 ft) is lower than Europe’s Caspian Sea (elevation −92 ft).
-131 < -92.
So, South America’s Valdes Peninsula < Europe’s Caspian Sea
Problem Solving + Applications – Page No. 148
What’s the Error?
Question 19.
In the game of golf, the player with the lowest score wins. Raheem, Erin, and Blake played a game of miniature golf. The table shows their scores compared to par.

At the end of the game, they wanted to know who had won.
Look at how they solved the problem. Find their error.
STEP 1: 0 is greater than both −1 and −5. Since Raheem had the highest score, he did not win.
STEP 2: −1 is less than −5, so Blake’s score was less than Erin’s score. Since Blake had the lowest score, he won the game.
Correct the error by ordering the scores from least to greatest.
So, _____ won. _____ came in second. _____ came in third.
Describe the error that the players made.
Type below:
__________
Answer:
Step 2 is wrong.
In step 2, they mentioned that -1 is less than −5. But -1 is greater than -5.
So, Erin won. Blake came in second. Raheem came in third.
Question 20.
Jasmine recorded the low temperatures for 3 cities.
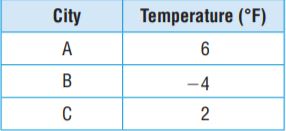
Draw a dot on the number line to represent the low temperature of each city. Write the letter of the city above the dot.
Type below:
__________
Answer:

Explanation:
6 > 2 > -4
Compare and Order Integers – Page No. 149
Compare the numbers. Write < or >.
Question 1.
–4 ____ –5
Answer:
-4 > -5
Explanation:
-4 is to the right of -5 on the number line.
So, -4 is greater than -5.
Question 2.
0 ____ –1
Answer:
0 > -1
Explanation:
0 is to the right of -1 on the number line.
So, 0 is greater than -1.
Question 3.
4 ____ –6
Answer:
4 > -6
Explanation:
4 is to the right of -6 on the number line.
So, 4 is greater than -6.
Question 4.
–9 ____ –8
Answer:
-9 < -8
Explanation:
-9 is to the left of -8 on the number line.
So, -9 is less than -8.
Question 5.
2 ____ –10
Answer:
2 > -10
Explanation:
2 is to the right of -10 on the number line.
So, 2 is greater than -10.
Question 6.
–12 ____ –11
Answer:
-12 < -11
Explanation:
-12 is to the left of -11 on the number line.
So, -12 is less than -11.
Question 7.
1 ____ –10
Answer:
1 > -10
Explanation:
1 is to the right of -10 on the number line.
So, 1 is greater than -10.
Order the numbers from least to greatest.
Question 8.
3, –2, –7
Type below:
__________
Answer:
-7, -2, 3
Explanation:
-7 is to the left of -2 on the number line. -2 is to the left of 3 on the number line.
So, -7 < -2 < 3
Question 9.
0, 2, –5
Type below:
__________
Answer:
-5, 0, 2
Explanation:
-5 is to the left of 0 on the number line. 0 is to the left of 2 on the number line.
So, -5 < 0 < 2
Question 10.
–9, –12, –10
Type below:
__________
Answer:
-12, -10, -9
Explanation:
-12 is to the left of -10 on the number line. -10 is to the left of -9 on the number line.
So, -12 < -10 < -9
Question 11.
–2, –3, –4
Type below:
__________
Answer:
-4, -3, -2
Explanation:
-4 is to the left of -3 on the number line. -3 is to the left of -2 on the number line.
So, -4 < -3 < -2
Question 12.
1, –6, –13
Type below:
__________
Answer:
-13, -6, 1
Explanation:
-13 is to the left of -6 on the number line. -6 is to the left of 1 on the number line.
So, -13 < -6 < 1
Question 13.
5, 7, 0
Type below:
__________
Answer:
0, 5, 7
Explanation:
0 is to the left of 5 on the number line. 5 is to the left of 7 on the number line.
So, 0 < 5 < 7
Question 14.
0, 13, –13
Type below:
__________
Answer:
-13, 0, 13
Explanation:
-13 is to the left of 0 on the number line. 0 is to the left of 13 on the number line.
So, -13 < 0 < 13
Question 15.
–11, 7, –5
Type below:
__________
Answer:
-11, -5, 7
Explanation:
-11 is to the left of -5 on the number line. -5 is to the left of 7 on the number line.
So, -11 < -5 < 7
Question 16.
–9, –8, 1
Type below:
__________
Answer:
-9, -8, 1
Explanation:
-9 is to the left of -8 on the number line. -8 is to the left of 1 on the number line.
So, -9 < -8 < 1
Problem Solving
Question 17.
Meg and Derek played a game. Meg scored –11 points, and Derek scored 4 points. Write a comparison to show that Meg’s score is less than Derek’s score.
Type below:
__________
Answer:
-11 < 4
Explanation:
Meg and Derek played a game. Meg scored -11 points, and Derek scored 4 points.
-11 < 4
Question 18.
Misha is thinking of a negative integer greater than −4. What number could she be thinking of?
Type below:
__________
Answer:
-3, -2, -1
Explanation:
Misha is thinking of a negative integer greater than −4.
-3, -2, -1
Question 19.
Explain how to use a number line to compare two negative integers. Give an example.
Type below:
__________
Answer:
-> On a number line, numbers always increase (become “more positive”) to the right and decrease (become “more negative”) to the left.
-> Numbers to the right are greater than numbers to the left and numbers to the left are less than numbers to the right.
Example: 2 > -10
2 is to the right of -10 on the number line.
So, 2 is greater than -10.
Lesson Check – Page No. 150

The chart shows the high temperatures for seven cities on one day in January.
Question 1.
Which city had the lower temperature, Helena or Chicago?
Type below:
__________
Answer:
Helena had a lower temperature
Explanation:
Helena = -1
Chicago = 2
-1 < 2
So, Helena had a lower temperature.
Question 2.
Write the temperatures of the following cities in order from greatest to least: Denver, Helena, Lansing.
Type below:
__________
Answer:
Lansing, Helena, Denver
Explanation:
Denver = -8
Helena = -1
Lansing = 3
3 > -1 > -8
So, Lansing, Helena, Denver is the answer.
Spiral Review
Question 3.
Fiona starts at the beginning of a hiking trail and walks \(\frac{4}{5}\) mile. She counts the mileage markers that are placed every \(\frac{1}{10}\) mile along the trail. How many markers does she count?
______ markers
Answer:
8 markers
Explanation:
Fiona starts at the beginning of a hiking trail and walks \(\frac{4}{5}\) mile. She counts the mileage markers that are placed every \(\frac{1}{10}\) mile along the trail.
Number of markers = (4/5)/(1/10) = 4/5 × 10 = 8
Question 4.
If Amanda hikes at an average speed of 2.72 miles per hour, how long will it take her to hike 6.8 miles?
______ hours
Answer:
2.5 hours
Explanation:
speed times time = distance
distance = 6.8
speed = 2.72
time = s
2.72 times s = 6.8
divide both sides by 2.72
s = 2.5
The answer is 2.5 hours
Question 5.
The area of a rectangle is 5 \(\frac{4}{5}\) square meters. The width of the rectangle is 2 \(\frac{1}{4}\) meter. Which is the best estimate for the length of the rectangle?
______ meters
Answer:
2 \(\frac{26}{45}\) meters
Explanation:
Since the area of a rectangle is, A = l × b
A = 5 \(\frac{4}{5}\) square meters
b = 2 \(\frac{1}{4}\) meter
5 \(\frac{4}{5}\) = l × 2 \(\frac{1}{4}\)
l = \(\frac{29 × 4}{9 × 5}\) = \(\frac{116}{45}\) = 2 \(\frac{26}{45}\)
Question 6.
Lillian bought 2.52 pounds of tomatoes and 1.26 pounds of lettuce to make a salad for 18 people. If each person got the same amount of salad, how much salad did each person get?
______ pounds per person
Answer:
0.21 pounds per person
Explanation:
Lillian bought 2.52 pounds of tomatoes and 1.26 pounds of lettuce to make a salad for 18 people.
2.52 pounds + 1.26 pounds = 3.78 pounds of salad ÷ 18 people = 0.21 pounds of salad per person
Share and Show – Page No. 153
Graph the number on the horizontal number line.
Question 1.
–2.25
Type below:
__________
Answer:

Explanation:
-2.25 is in between -2 and -3.
-2.25 is between -2 and -2.5
Question 2.
–1 \(\frac{5}{8}\)
Type below:
__________
Answer:

Explanation:
-1 \(\frac{5}{8}\) is in between -1 and -2.
-1 \(\frac{5}{8}\) is closer to -2.
Question 3.
\(\frac{1}{2}\)
Type below:
__________
Answer:
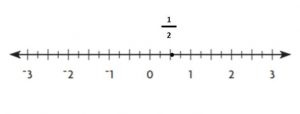
Explanation:
\(\frac{1}{2}\) is in between 0 and 1
\(\frac{1}{2}\) = 0.5
On Your Own
Practice: Copy and Solve Graph the number on a vertical number line.
Question 4.
0.6
Type below:
__________
Answer:

Explanation:
0.6 is in between 0 and 1.
0.6 is closer to 1
Question 5.
–1.25
Type below:
__________
Answer:
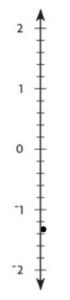
Explanation:
-1.25 is in between -1 and -2
-1.25 is closer to -1.
Question 6.
–1 \(\frac{1}{2}\)
Type below:
__________
Answer:
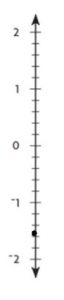
Explanation:
-1 \(\frac{1}{2}\) is in between -1 and -2
-1 \(\frac{1}{2}\) = -1.5
Question 7.
0.3
Type below:
__________
Answer:
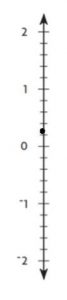
Explanation:
0.3 is in between 0 and 1
0.3 is closer to 0
Question 8.
–0.7
Type below:
__________
Answer:
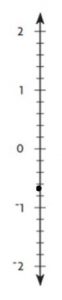
Explanation:
-0.7 is in between 0 and -1
-0.7 is closer to -1
Question 9.
1.4
Type below:
__________
Answer:
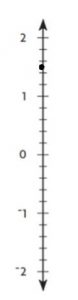
Explanation:
1.4 is in between 1 and 2
1.4 is closer to 1
Question 10.
−0.5
Type below:
__________
Answer:

Explanation:
−0.5 is in between 0 and -1
Question 11.
− \(\frac{1}{4}\)
Type below:
__________
Answer:
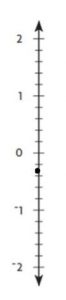
Explanation:
− \(\frac{1}{4}\) is in between 0 and -1
-0.25 is closer to 0
State whether the numbers are on the same or opposite sides of zero.
Question 12.
−1.38 and 2.9
Type below:
__________
Answer:
Opposite
Explanation:
-1.38 is a negative number.
2.9 is a positive number.
So, both numbers are on opposite sides of zero.
Question 13.
−3 \(\frac{9}{10}\) and −0.99
Type below:
__________
Answer:
Same
Explanation:
−3 \(\frac{9}{10}\) is a negative number.
−0.99 is a negative number.
So, both numbers are on the same sides of zero.
Question 14.
\(\frac{5}{6}\) and −4.713
Type below:
__________
Answer:
Opposite
Explanation:
−4.713 is a negative number.
\(\frac{5}{6}\) is a positive number.
So, both numbers are on opposite sides of zero.
Identify a decimal and a fraction in simplest form for the point.

Question 15.
Point A
Type below:
__________
Answer:
-1.0
Explanation:
The point A is located at -1.0 = -1
Question 16.
Point B
Type below:
__________
Answer:
0.75 = 3/4
Explanation:
Point B is between 0.5 and 1. It is 0.75
Question 17.
Point C
Type below:
__________
Answer:
-0.25 = 1/4
Explanation:
Point C is in between 0 and -0.5
-0.25
Question 18.
Point D
Type below:
__________
Answer:
-1.25 = 5/4
Explanation:
Point D is in between -1 and -1.5.
-1.25
Question 19.
The roots of 6 corn plants grew to −3.54 feet, −2 \(\frac{4}{5}\) feet, −3.86 feet, −4 \(\frac{1}{8}\) feet, −4.25 feet, and −2 \(\frac{2}{5}\) feet. How many corn plants had roots between 3 and 4 feet deep?
______ plants
Answer:
2 plants
Explanation:
The roots of 6 corn plants grew to −3.54 feet, −2 \(\frac{4}{5}\) feet, −3.86 feet, −4 \(\frac{1}{8}\) feet, −4.25 feet, and −2 \(\frac{2}{5}\) feet.
−3.54 feet, −3.86 feet,
2 corn plants had roots between 3 and 4 feet deep.
Problem Solving + Applications – Page No. 154
A star’s magnitude is a number that measures the star’s brightness. Use the table of star magnitudes for 20–22.
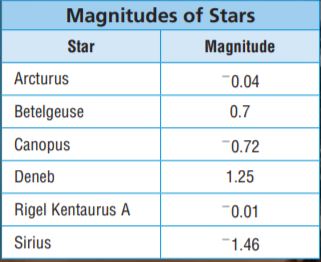
Question 20.
Between what two integers is the magnitude of Canopus?
Type below:
__________
Answer:
-0.72 is between -0.04 and -1.46
Explanation:
Canopus = -0.72
-0.72 is between -0.04 and -1.46
Question 21.
Model Mathematics
Graph the magnitude of Betelgeuse on the number line.
Type below:
__________
Answer:

Explanation:
Betelgeuse = 0.7
Question 22.
What’s the Error?
Jacob graphed the magnitude of Sirius on the number line. Explain his error. Then graph the magnitude correctly.
Type below:
__________
Answer:
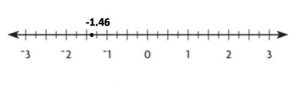
Explanation:
Sirius = -1.46
Question 23.
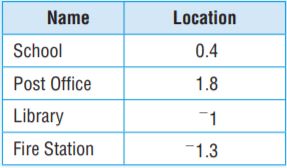
The flag pole is located at point 0 on a map of Orange Avenue. Other points of interest on Orange Avenue are located on the number line based on their distances, in miles to the right of the flag pole (positive numbers) or to the left of the flag pole (negative numbers). Graph and label each location on the number line.
Type below:
__________
Answer:

Explanation:
0.4 is the right side of the 0.
1.8 is the right side of the 0.
-1 is the left side of the 0.
-1.3 is the left side of the 0.
Rational Numbers and the Number Line – Page No. 155
Graph the number on the number line.
Question 1.
−2 \(\frac{3}{4}\)
Type below:
__________
Answer:
Explanation:
The number is between the integers -3 and -2.
It is closer to the integer -3.
Question 2.
\(\frac{-1}{4}\)
Type below:
__________
Answer:
Explanation:
The number is between the integers -0.3 and -0.2.
It is closer to the integer -0.25.
Question 3.
−0.5
Type below:
__________
Answer:
![]()
Explanation:
The number is between integers 0 and -1.
It is closer to the integer -0.5.
Question 4.
1.75
Type below:
__________
Answer:

Explanation:
The number is between integers 1 and 2.
It is closer to the integer 1.75.
Question 5.
1 \(\frac{1}{2}\)
Type below:
__________
Answer:
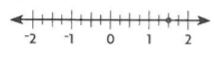
Explanation:
The number is between integers 1 and 2.
It is closer to the integer 1.5.
State whether the numbers are on the same or opposite sides of zero.
Question 6.
−2.4 and 2.3
Type below:
__________
Answer:
Opposite
Explanation:
-2.4 is a negative number.
2.3 is a positive number.
So, both numbers are on opposite sides of zero.
Question 7.
−2 \(\frac{1}{5}\) and −1
Type below:
__________
Answer:
Same
Explanation:
−2 \(\frac{1}{5}\) is a negative number.
-1 is a negative number.
So, both numbers are on the same sides of zero.
Question 8.
−0.3 and 0.3
Type below:
__________
Answer:
opposite
Explanation:
-0.3 is a negative number.
0.3 is a positive number.
So, both numbers are on opposite sides of zero.
Question 9.
0.44 and \(\frac{2}{3}\)
Type below:
__________
Answer:
Same
Explanation:
0.44 is a positive number.
\(\frac{2}{3}\) is a positive number.
So, both numbers are on the same sides of zero.
Write the opposite of the number.
Question 10.
−5.23
Type below:
__________
Answer:
5.23
Explanation:
The opposite number of -5.23 is 5.23
Question 11.
\(\frac{4}{5}\)
Type below:
__________
Answer:
–\(\frac{4}{5}\)
Explanation:
The opposite number of \(\frac{4}{5}\) is –\(\frac{4}{5}\)
Question 12.
−5
Type below:
__________
Answer:
5
Explanation:
The opposite number of -5 is 5
Question 13.
−2 \(\frac{2}{3}\)
Type below:
__________
Answer:
2 \(\frac{2}{3}\)
Explanation:
The opposite number of −2 \(\frac{2}{3}\) is 2 \(\frac{2}{3}\)
Problem Solving
Question 14.
The outdoor temperature yesterday reached a low of −4.5° F. Between what two integers was the temperature?
Type below:
__________
Answer:
An integer is a whole number. -4.5 is not a whole number.
-4.5 is in between -4 and the integer below it is -5.
Question 15.
Jacob needs to graph −6 \(\frac{2}{5}\) on a horizontal number line. Should he graph it to the left or right of −6?
Type below:
__________
Answer:
left
Explanation:
It will on the left because it is negative and on a number line the left side is the least side.
Question 16.
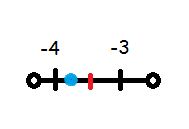
Describe how to plot −3 \(\frac{3}{4}\) on a number line.
Type below:
__________
Answer:
On the number line, negative numbers go to the left. Since -3 3/4 is negative, go 3 spaces to the left.
If there are half marks in between the numbers, plot the point near the half mark. If it’s -3 3/4, count 3 spaces, then go to the half mark of -3 to -4, and plot the 3/4 in between the -3 and -4 half mark. If there is no half mark, place it near the -4 mark.
The red line represents the half mark, the blue line represents where the point would go. Notice how when negative, the numbers go higher as they go left.
Lesson Check – Page No. 156
Question 1.
What number is the opposite of 0.2?
Type below:
__________
Answer:
-0.2
Explanation:
The opposite of 0.2 is -0.2
Question 2.
Between which two integers would you locate −3.4 on a number line?
Type below:
__________
Answer:
-3.4 is located between -3 and -4
Explanation:
Positive 3.4 lies between 3 and 4 on the number line. It is more than 3 but less than 4. 3.4 is further from 0 than just 3. In the same way and because of the symmetrical arrangement of numbers on the number line, -3.4 lies between -3 and -4.
Spiral Review
Question 3.
Yemi used these pattern blocks to solve a division problem. He found a quotient of 7. Which division problem was he solving?
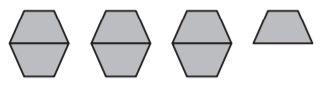
Type below:
__________
Answer:
7
Explanation:
3 1/2 ÷ 1/2
First, we transform the mixed number into a fraction, 3 1/2 = 7/2
Then, we divide
7/2 ÷ 1/2 = 7
The quotient of the first division is 7.
Question 4.
Eric had 2 liters of water. He gave 0.42 liter to his friend and then drank 0.32 liter. How much water does he have left?
______ liters
Answer:
1.26 liters
Explanation:
Eric had 2 liters of water. He gave 0.42 liter to his friend and then drank 0.32 liter.
2 – 0.42 – 0.32 = 1.26 L
Question 5.
To pass a math test, students must correctly answer at least 0.6 of the questions. Donald’s score is \(\frac{5}{8}\), Karen’s score is 0.88, Gino’s score is \(\frac{3}{5}\) and Sierra’s score is \(\frac{4}{5}\). How many of the students passed the test?
Type below:
__________
Answer:
4
Explanation:
Donald’s score of 5/8 is equal to 0.625.
Gino scored 3/5 which is 0.6.
Sierra’s score of 4/5 equals 0.8.
Karen’s score is already given, and 0.88 is greater than 0.6.
None of the students obtained lower than 0.6.
If at least does not include scores equal to 0.6, and only scores greater than 0.6, then Gino possibly failed this math test.
If a passing score is equal to or greater than 0.6, then all four students passed the test.
Question 6.
Jonna mixes \(\frac{1}{4}\) gallon of orange juice and \(\frac{1}{2}\) gallon of pineapple juice to make punch. Each serving is \(\frac{1}{16}\) gallon. How many servings can Jonna make?
_____ servings
Answer:
12 servings
Explanation:
The number of a gallon of orange juice is mixed to make punch is given by 1/4
The number of a gallon of pineapple juice is mixed to make punch is given by 1/2
The number of gallon in each serving is given by 1/16
1/4 + 1/2 = 3/4
3/4 ÷ 1/16 = 12
So, there are 12 servings which can be made by Jonna.
Share and Show – Page No. 159
Compare the numbers. Write < or >.
Question 1.
−0.3 _____ 0.2
Answer:
-0.3 < 0.2
Explanation:
-0.3 is to the left of 0.2 on the number line.
So, -0.3 is less than 0.2.
Question 2.
\(\frac{1}{3}\) _____ \(\frac{−2}{5}\)
Answer:
\(\frac{1}{3}\) > \(\frac{−2}{5}\)
Explanation:
\(\frac{1}{3}\) is to the right of \(\frac{−2}{5}\) on the number line.
So, \(\frac{1}{3}\) is greater than \(\frac{−2}{5}\).
Question 3.
−0.8 _____ −0.5
Answer:
−0.8 < −0.5
Explanation:
-0.8 is to the left of -0.5 on the number line.
So, -0.8 is less than -0.5.
Question 4.
\(\frac{−3}{4}\) _____ −0.7
Answer:
\(\frac{−3}{4}\) < −0.7
Explanation:
\(\frac{−3}{4}\) is to the left of −0.7 on the number line.
So, \(\frac{−3}{4}\) is less than −0.7.
Order the numbers from least to greatest.
Question 5.
3.6, −7.1, −5.9
Type below:
__________
Answer:
-7.1, -5.9, 3.6
Explanation:
-7.1 is to the left of -5.9 on the number line. -5.9 is to the left of 3.6 on the number line.
So, -7.1 < -5.9 < 3.6
Question 6.
\(\frac{-6}{7}, \frac{1}{9}, \frac{-2}{3}\)
Type below:
__________
Answer:
\(\frac{-6}{7}, \frac{-2}{3}, \frac{1}{9}\)
Explanation:
-6/7 = -0.857
1/9 = 0.111
-2/3 = -0.666
-6/7 is to the left of -2/3 on the number line. -2/3 is to the left of 1/9 on the number line.
So, -6/7 < -2/3 < 1/9
Question 7.
−5 \(\frac{1}{4}\), −6.5, −5.3
Type below:
__________
Answer:
-6.5, -5.3, −5 \(\frac{1}{4}\)
Explanation:
−5 \(\frac{1}{4}\) = -21/4 = -5.25
-6.5 is to the left of -5.3 on the number line. -5.3 is to the left of -5 \(\frac{1}{4}\) on the number line.
-6.5 < -5.3 < -5.25
On Your Own
Compare the numbers. Write < or >.
Question 8.
\(\frac{−1}{2}\) _____ \(\frac{−3}{7}\)
Answer:
\(\frac{−1}{2}\) < \(\frac{−3}{7}\)
Explanation:
\(\frac{−1}{2}\) = -0.5
\(\frac{−3}{7}\) = -0.428
\(\frac{−1}{2}\) is to the left of \(\frac{−3}{7}\) on the number line.
So, \(\frac{−1}{2}\) is less than \(\frac{−3}{7}\).
Question 9.
−23.7 _____ −18.8
Answer:
−23.7 < −18.8
Explanation:
−23.7 is to the left of −18.8 on the number line.
So, −23.7 is less than −18.8.
Question 10.
−3 \(\frac{1}{4}\) _____ −4.3
Answer:
−3 \(\frac{1}{4}\) > −4.3
Explanation:
−3 \(\frac{1}{4}\) = -13/4 = -3.25
−3 \(\frac{1}{4}\) is to the right of −4.3 on the number line.
So, −3 \(\frac{1}{4}\) is greater than −4.3.
Order the numbers from greatest to least.
Question 11.
−2.4, 1.9, −7.6
Type below:
__________
Answer:
1.9, -2.4, -7.6
Explanation:
1.9 is to the right of -2.4 on the number line. -2.4 is to the right of -7.6 on the number line.
So, 1.9 > -2.4 > -7.6
Question 12.
\(\frac{-2}{5}, \frac{-3}{4}, \frac{-1}{2}\)
Type below:
__________
Answer:
\(\frac{-2}{5}, \frac{-1}{2}, \frac{-3}{4}\)
Explanation:
-2/5 = -0.4; -3/4 = -0.75; -1/2 = -0.5
-2/5 is to the right of -1/2 on the number line. -1/2 is to the right of -3/4 on the number line.
So, -2/5 > -1/2 > -3/4
Question 13.
3, −6 \(\frac{4}{5}\), −3 \(\frac{2}{3}\)
Type below:
__________
Answer:
3, −3 \(\frac{2}{3}\), −6 \(\frac{4}{5}\)
Explanation:
−6 \(\frac{4}{5}\) = -34/5 = -6.8
−3 \(\frac{2}{3}\) = -11/3 = -3.666
3 is to the right of -3 \(\frac{2}{3}\) on the number line. -3 \(\frac{2}{3}\) is to the right of −6 \(\frac{4}{5}\) on the number line.
So, 3 > −3 \(\frac{2}{3}\) > −6 \(\frac{4}{5}\)
Question 14.
Last week, Wednesday’s low temperature was −4.5°F, Thursday’s low temperature was −1.2°F, Friday’s low temperature was −2.7°F, and Saturday’s low temperature was 0.5°F. The average low temperature for the week was −1.5°F. How many of these days had low temperatures less than the average low temperature for the week?
_____ days
Answer:
2 days
Explanation:
Last week, Wednesday’s low temperature was −4.5°F, Thursday’s low temperature was −1.2°F, Friday’s low temperature was −2.7°F, and Saturday’s low temperature was 0.5°F. The average low temperature for the week was −1.5°F.
-4.5 < -1.5; -2.7 < -1.5
2 days had low temperatures less than the average low temperature for the week.
Question 15.
Use Symbols Write a comparison using < or > to show the relationship between an elevation of −12 \(\frac{1}{2}\) ft and an elevation of −16 \(\frac{5}{8}\) ft.
Type below:__________
Answer:
−12 \(\frac{1}{2}\) ft > −16 \(\frac{5}{8}\) ft
Explanation:
−12 \(\frac{1}{2}\) = -25/2 = -12.5
−16 \(\frac{5}{8}\) = -133/8 = -16.625
-12.5 > -16.625
Problem Solving + Applications – Page No. 160
Elevations, in miles, are given for the lowest points below sea level for 4 bodies of water. Use the table for 16–19.
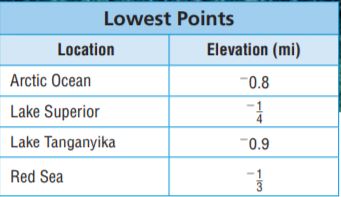
Question 16.
The lowest point of which has the greater elevation, the Arctic Ocean or Lake Tanganyika?
Type below:
__________
Answer:
Arctic Ocean has the greater elevation
Explanation:
Arctic Ocean = -0.8
Lake Tanganyika = -0.9
-0.8 > -0.9
Arctic Ocean has the greater elevation
Question 17.
Which has a lower elevation, the lowest point of Lake Superior or a point at an elevation of \(\frac{2}{5}\) mi?
Type below:
__________
Answer:
Lake Superior has a lower elevation
Explanation:
Lake Superior = -1/4 = -0.25
\(\frac{2}{5}\) = 0.4
-0.25 < 0.4
Lake Superior has a lower elevation
Question 18.
List the elevations in order from least to greatest.
Type below:
__________
Answer:
-0.9, -0.8, -1/3, -1/4
Explanation:
Article Ocean = -0.8
Lake Superior = -1/4 = -0.25
Lake Tanganyika = -0.9
Red Sea = -1/3 = -0.333
-0.9 < -0.8 < -0.333 < -0.25
Question 19.
A shipwreck is found at an elevation of – 0.75 mile. In which bodies of water could the shipwreck have been found?
Type below:
__________
Answer:
Article Ocean
Explanation:
-0.75 is closer to -0.8
Article Ocean = -0.8
Question 20.
Circle <, >, or =.
20a. \(\frac{−3}{5}\) Ο \(\frac{−4}{5}\)
20b. \(\frac{−2}{5}\) Ο \(\frac{−3}{4}\)
20c. −6.5 Ο −4.2
20d. −2.4 Ο −3.7
\(\frac{−3}{5}\) _____ \(\frac{−4}{5}\)
\(\frac{−2}{5}\) _____ \(\frac{−3}{4}\)
−6.5 _____ −4.7
−2.4 _____ −3.7
Answer:
\(\frac{−3}{5}\) > \(\frac{−4}{5}\)
\(\frac{−2}{5}\) > \(\frac{−3}{4}\)
−6.5 < −4.7
−2.4 > −3.7
Explanation:
-3/5 = -0.6; -4/5 = -0.8
-0.6 > -0.8
-2/5 = -0.4; -3/4 = -0.75
-0.4 > -0.75
-6.5 < -4.7
-2.4 > -3.7
Compare and Order Rational Numbers – Page No. 161
Compare the numbers. Write < or >.
Question 1.
−1\(\frac{1}{2}\) _____ \(\frac{−1}{2}\)
Answer:
−1\(\frac{1}{2}\) < \(\frac{−1}{2}\)
Explanation:
−1\(\frac{1}{2}\) = -3/2 = – 1.5
\(\frac{−1}{2}\) = -0.5
-1.5 < -0.5
Question 2.
0.1 _____ −1.9
Answer:
0.1 > −1.9
Explanation:
0.1 is to the right of -1.9 on the number line.
So, 0.1 is greater than -1.9.
Question 3.
0.4 _____ \(\frac{−1}{2}\)
Answer:
0.4 > \(\frac{−1}{2}\)
Explanation:
0.4 is to the right of \(\frac{−1}{2}\) on the number line.
So, 0.4 is greater than \(\frac{−1}{2}\).
Question 4.
\(\frac{2}{5}\) _____ 0.5
Answer:
\(\frac{2}{5}\) < 0.5
Explanation:
2/5 = 0.4
0.4 < 0.5
Order the numbers from least to greatest.
Question 5.
0.2, −1.7, −1
Type below:
__________
Answer:
-1.7, -1, 0.2
Explanation:
-1.7 is to the left of -1 on the number line. -1 is to the left of 0.2 on the number line.
So, -1.7 < -1 < 0.2
Question 6.
\(2 \frac{3}{4}, \frac{-3}{5}, 1 \frac{3}{4}\)
Type below:
__________
Answer:
\( \frac{-3}{5}, 1\frac{3}{4}, 2 \frac{3}{4}\)
Explanation:
2 3/4 = 11/4 = 2.75
-3/5 = – 0.6
1 3/4 = 7/4 = 1.75
-0.6 < 1.75 < 2.75
Question 7.
−0.5, −1 \(\frac{2}{3}\), −2.7
Type below:
__________
Answer:
-2.7, −1 \(\frac{2}{3}\), -0.5
Explanation:
−1 \(\frac{2}{3}\) = -5/3 = -1.666
-2.7 < -1.66, -0.5
Order the numbers from greatest to least.
Question 8.
−1, \(\frac{−5}{6}\), 0
Type below:
__________
Answer:
0, \(\frac{−5}{6}\), -1
Explanation:
\(\frac{−5}{6}\) = -0.8333
0 is to the right of \(\frac{−5}{6}\) on the number line. \(\frac{−5}{6}\) is to the right of -1 on the number line.
So, 0 > \(\frac{−5}{6}\) > -1
Question 9.
\(1.82, \frac{-2}{5}, \frac{4}{5}\)
Type below:
__________
Answer:
\(1.82, \frac{4}{5}, \frac{-2}{5}\)
Explanation:
-2/5 = -0.4
4/5 = 0.8
1.82
1.82 > 0.8 > -0.4
Question 10.
−2.19, −2.5, 1.1
Type below:
__________
Answer:
1.1, -2.19, -2.5
Explanation:
1.1 is to the right of -2.19 on the number line. -2.19 is to the right of -2.5 on the number line.
So, 1.1 > -2.19 > -2.5
Write a comparison using < or > to show the relationship between the two values.
Question 11.
an elevation of −15 m and an elevation of −20.5 m
Type below:
__________
Answer:
-15m > -20.5m
Explanation:
-15 is to the right of -20.5 on the number line.
-15m > -20.5m
Question 12.
a balance of $78 and a balance of −$42
Type below:
__________
Answer:
$42 < $78
Explanation:
$42 is to the left of $78 on the number line.
So, $42 is less than $78.
Question 13.
a score of −31 points and a score of −30 points
Type below:
__________
Answer:
-31 points < -30 points
Explanation:
-31 is to the left of -30 on the number line.
So, -31 is less than -30.
Problem Solving
Question 14.
The temperature in Cold Town on Monday was 1°C. The temperature in Frosty Town on Monday was −2°C. Which town was colder on Monday?
Type below:
__________
Answer:
Frosty Town
Explanation:
The temperature in Cold Town on Monday was 1°C. The temperature in Frosty Town on Monday was −2°C.
Frosty Town town was colder on Monday.
Question 15.
Stan’s bank account balance is less than −$20.00 but greater than −$21.00. What could Stan’s account balance be?
Type below:
__________
Answer:
From -$20.99 to -$20.01
Explanation:
Stan’s bank account balance is less than −$20.00 but greater than −$21.00. The possible answer is From -$20.99 to -$20.01
Question 16.
Describe two situations in which it would be helpful to compare or order positive and negative rational numbers.
Type below:
__________
Answer:
1) negative numbers in weather reports and on food packaging. The temperature -5°C is ‘negative five degrees’ and it means 5 degrees below zero.
2) When you spend more money than you have in your bank account it shows up as a negative number.
Lesson Check – Page No. 162
Question 1.
The low temperature was —1.8 °C yesterday and −2.1 °C today. Use the symbols < or > to show the relationship between the temperatures.
Type below:
__________
Answer:
The low temperature was —1.8 °C yesterday and −2.1 °C today.
-1.8 > -2.1
Question 2.
The scores at the end of a game are shown. List the scores in order from greatest to least.
Vince: −0.5
Allison: \(\frac{3}{8}\)
Mariah: \(\frac{−7}{20}\)
Type below:
__________
Answer:
\(\frac{3}{8}\), -0.5, \(\frac{−7}{20}\)
Explanation:
\(\frac{3}{8}\) = 0.375
\(\frac{−7}{20}\) = -0.35
-0.5
\(\frac{3}{8}\) > -0.5 > -0.35
Spiral Review
Question 3.
Simone bought 3.42 pounds of green apples and 2.19 pounds of red apples. She used 3 pounds to make a pie. How many pounds of apples are left?
_____ pounds
Answer:
2.61 pounds
Explanation:
She bought 3.42 pounds of green apples, then you can subtract 3 lbs off of that, so she bought .42 lbs of green apples and 2.19 lbs red apples
So now, you just need to add .42 and 2.19
.42 + 2.19 = 2.61, so she has 2.61 lbs of apples left
Question 4.
Kwan bought three rolls of regular wrapping paper with 6.7 square meters of paper each. He also bought a roll of fancy wrapping paper containing 4.18 square meters. How much paper did he have altogether?
_____ square meters
Answer:
24.28 square meters
Explanation:
He bought 3 rolls of regular wrapping paper with 6.7 m². Then the total of this paper is: 3 × 6.7 = 20.1
He also bought a roll of fancy wrapping with 4.18 m². Therefore, to calculate the amount of paper he had together (which you can call ), you must add 20.1 m² and 4.18 m²,
x = 20.1 + 41.8 = 24.28
Question 5.
Eddie needs 223 cups of flour for one batch of pancakes. How much flour does he need for 212 batches?
_____ \(\frac{□}{□}\) cups
Answer:
6\(\frac{4}{6}\) cups
Explanation:
For 1 batch of pancake = 2 2/3 = 8/3 cups
For 2 1/2 = 5/2 pancake = 8/3 × 5/2 = 40/6 cups = 6 4/6 cups
Question 6.
Tommy notices that he reads \(\frac{2}{3}\) page in a minute. At that rate, how long will it take him to read 12 pages?
_____ minutes
Answer:
18 minutes
Explanation:
It will take him 18 minutes.
2/3 of a page in 18 minutes= 12 pages read
Mid-Chapter Checkpoint – Vocabulary – Page No. 163
Choose the best term from the box to complete the sentence.
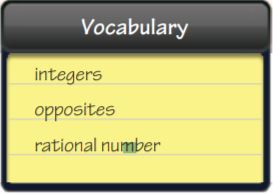
Question 1.
Any number that can be written as \(\frac{a}{b}\), where a and b are integers and b≠0 is called a(n) _____.
Type below:
__________
Answer:
rational number
Question 2.
The set of whole numbers and their opposites is the set of _____.
Type below:
__________
Answer:
Integers
Concepts and Skills
Write the opposite of the integer.
Question 3.
−72
Type below:
__________
Answer:
72
Explanation:
The integer −72 is on the left side of 0.
So, the opposite of -72 is 72
Question 4.
0
Type below:
__________
Answer:
0
Explanation:
Opposite of 0 is 0
Question 5.
−31
Type below:
__________
Answer:
31
Explanation:
The integer −31 is on the left side of 0.
So, the opposite of -31 is 31
Question 6.
27
Type below:
__________
Answer:
Explanation:
The integer 27 is on the right side of 0.
So, the opposite of 27 is -27
Name the integer that represents the situation, and tell what 0 represents in that situation.

Question 7.
Type below:
__________
Answer:
Integer: 278
0 represents: Neither loses or gains in the video game.
Question 8.
Type below:
__________
Answer:
Integer: -8 degrees
0 represents: No change in the temperature.
Compare the numbers. Write < or >.
Question 9.
3 _____ −4
Answer:
3 > −4
Explanation:
3 is to the right of -4 on the number line.
So, 3 is greater than -4.
Question 10.
−6 _____ −5
Answer:
−6 < −5
Explanation:
-6 is to the left of -5 on the number line.
So, -6 is less than -5.
Question 11.
5 _____ −6
Answer:
5 > −6
Explanation:
5 is to the right of -6 on the number line.
So, 5 is greater than -6.
Question 12.
\(\frac{1}{3}\) _____ \(\frac{1}{2}\)
Answer:
\(\frac{1}{3}\) < \(\frac{1}{2}\)
Explanation:
\(\frac{1}{3}\) is to the left of \(\frac{1}{2}\) on the number line.
So, \(\frac{1}{3}\) is less than \(\frac{1}{2}\).
Question 13.
−3.1 _____ −4.3
Answer:
−3.1 >−4.3
Explanation:
-3.1 is to the right of -4.3 on the number line.
So, -3.1 is greater than -4.3.
Question 14.
1\(\frac{3}{4}\) _____ −2\(\frac{1}{2}\)
Answer:
1\(\frac{3}{4}\) >−2\(\frac{1}{2}\)
Explanation:
1\(\frac{3}{4}\) is to the right of −2\(\frac{1}{2}\) on the number line.
So, 1\(\frac{3}{4}\) is greater than −2\(\frac{1}{2}\).
Order the numbers.
Question 15.
5, −2, −8
Type below:
__________
Answer:
-8, -2, 5
Explanation:
-8 is to the left of -2 on the number line. -2 is to the left of 5 on the number line.
So, -8 < -2 < 5
Question 16.
0, −3, 1
Type below:
__________
Answer:
-3, 0, 1
Explanation:
-3 is to the left of 0 on the number line. 0 is to the left of 1 on the number line.
So, -3 < 0 < 1
Question 17.
−7, −6, −11
Type below:
__________
Answer:
-11, -7, -6
Explanation:
-11 is to the left of -7 on the number line. -7 is to the left of -6 on the number line.
So, -11 < -7 < -6
Question 18.
2.5, −1.7, −4.3
Type below:
__________
Answer:
-4.3, -1.7, 2.5
Explanation:
-4.3 is to the left of -1.7 on the number line. -1.7 is to the left of 2.5 on the number line.
So, -4.3 < -1.7 < 2.5
Question 19.
\(\frac{2}{3} \cdot \frac{1}{4}, \frac{5}{12}\)
Type below:
__________
Answer:
\(\frac{1}{4} \cdot \frac{5}{12}, \frac{2}{3}\)
Explanation:
2/3 = 0.666
1/4 = 0.25
5/12 = 0.4166
1/4 < 5/12 < 2/3
Question 20.
−5.2, −3.8, −9.4
Type below:
__________
Answer:
−9.4, −5.2, −3.8
Explanation:
-9.4 is to the left of -5.2 on the number line. -5.2 is to the left of -3.8 on the number line.
So, -9.4 < -5.2 < -3.8
Page No. 164
Question 21.
Judy is scuba diving at −7 meters, Nelda is scuba diving at −9 meters, and Rod is scuba diving at −3 meters. List the divers in order from the deepest diver to the diver who is closest to the surface.
Type below:
__________
Answer:
Judy is scuba diving at −7 meters, Nelda is scuba diving at −9 meters, and Rod is scuba diving at −3 meters.
the higher the value of the negative number, the deepest the diver is.
Nelda (-9)- Judy (-7) -Rod (-3)
Question 22.
A football team gains 8 yards on their first play. They lose 12 yards on the next play. What two integers represent the two plays?
Type below:
__________
Answer:
A football team gains 8 yards on their first play. +8
They lose 12 yards on the next play. -12
The 2 integers are positive 8 and negative 12
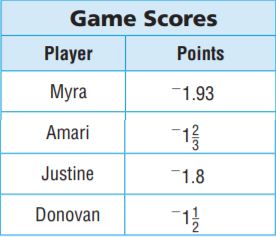
Question 23.
The player who scores the closest to 0 points wins the game. The scores of four players are given in the table. Who won the game?
Type below:
__________
Answer:
Donovan won the game
Explanation:
Donovan because he has-1.5
Myra has -1.93
Amari has -1.66666666
Justine has -1.8
-1.5 is the closest to 0
Question 24.
Which point on the graph represents −3 \(\frac{3}{4}\) ? What number does point C represent?

Type below:
__________
Answer:
A
Explanation:
−3 \(\frac{3}{4}\) = -15/4 = -3.75
-3.75 is in between -3 and -4.
So, point A is the correct answer
Share and Show – Page No. 167
Find the absolute value.
Question 1.
|−2|
Type below:
__________
Answer:
2
Explanation:
The distance from 0 to the point I graphed is 2 units.
|−2| = 2
Question 2.
|6|
Type below:
__________
Answer:
6
Explanation:
The distance from 0 to the point I graphed is 6 units.
|6| = 6
Question 3.
|−5|
Type below:
__________
Answer:
5
Explanation:
The distance from 0 to the point I graphed is 6 units.
|-5| = 5
Question 4.
|−11|
Type below:
__________
Answer:
11
Explanation:
The distance from 0 to the point I graphed is 6 units.
|-11| = 11
Question 5.
|9|
Type below:
__________
Answer:
9
Explanation:
The distance from 0 to the point I graphed is 6 units.
|9| = 9
Question 6.
|−15|
Type below:
__________
Answer:
15
Explanation:
The distance from 0 to the point I graphed is 6 units.
|-15| = 15
On Your Own
Find the absolute value.
Question 7.
|−37|
Type below:
__________
Answer:
37
Explanation:
The distance from 0 to the point I graphed is 6 units.
|-37| = 37
Question 8.
|1.8|
Type below:
__________
Answer:
1.8
Explanation:
The distance from 0 to the point I graphed is 6 units.
|1.8| = 1.8
Question 9.
|\(\frac{−2}{3}\)|
Type below:
__________
Answer:
|\(\frac{2}{3}\)|
Explanation:
The distance from 0 to the point I graphed is 6 units.
||\(\frac{−2}{3}\)|| = |\(\frac{2}{3}\)|
Question 10.
|−6.39|
Type below:
__________
Answer:
6.39
Explanation:
The distance from 0 to the point I graphed is 6 units.
|-6.39| = 6.39
Question 11.
|−5\(\frac{7}{8}\)|
Type below:
__________
Answer:
5\(\frac{7}{8}\)
Explanation:
The distance from 0 to the point I graphed is 5\(\frac{7}{8}\) units.
|−5\(\frac{7}{8}\)| = 5\(\frac{7}{8}\)
Find all numbers with the given absolute value.
Question 12.
13
Type below:
__________
Answer:
13 and -13
Explanation:
13 and -13 are at the same distance from 0.
Question 13.
\(\frac{5}{6}\)
Type below:
__________
Answer:
\(\frac{5}{6}\) and \(\frac{-5}{6}\)
Explanation:
\(\frac{5}{6}\) and \(\frac{-5}{6}\) are at the same distance from 0.
Question 14.
14.03
Type below:
__________
Answer:
14.03 and -14.03
Explanation:
14.03 and -14.03 are at the same distance from 0.
Question 15.
0.59
Type below:
__________
Answer:
0.59 and -0.59
Explanation:
0.59 and -0.59 are at the same distance from 0.
Question 16.
3\(\frac{1}{7}\)
Type below:
__________
Answer:
3\(\frac{1}{7}\) and -3\(\frac{1}{7}\)
Explanation:
3\(\frac{1}{7}\) and -3\(\frac{1}{7}\) are at the same distance from 0.
Use Reasoning Algebra Find the missing number or numbers to make the statement true.
Question 17.
|?| = 10
Type below:
__________
Answer:
10 and -10
Explanation:
|-10| = 10
|10| = 10
Question 18.
|?| = 1.78
Type below:
__________
Answer:
1.78 and -1.78
Explanation:
|-1.78| = 1.78
|1.78| = 1.78
Question 19.
|?| = 0
Type below:
__________
Answer:
0
Explanation:
|0| = 0
Question 20.
|?| = \(\frac{15}{16}\)
Type below:
__________
Answer:
\(\frac{-15}{16}\) and \(\frac{15}{16}\)
Explanation:
|\(\frac{-15}{16}\)| = \(\frac{15}{16}\)
|\(\frac{15}{16}\)| = \(\frac{15}{16}\)
Question 21.
Find all of the integers whose absolute value is less than |–4|.
Type below:
__________
Answer:
3, 2, 1, 0
Explanation:
The absolute value of |–4| = 4.
3, 2, 1, 0 are the integers whose absolute value is less than |–4|.
Unlock The Problem – Page No. 168
Question 22.
The Blue Ridge Trail starts at Park Headquarters in Big Bear Park and goes up the mountain. The Green Creek Trail starts at Park Headquarters and goes down the mountain. The table gives elevations of various points of interest in relation to Park Headquarters. How many points of interest are less than 1 kilometer above or below Park Headquarters?
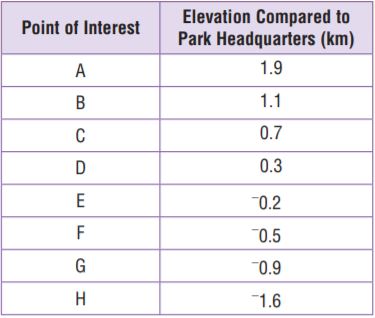
a. How can you find how far above or below Park Headquarters a given point of interest is located?
Type below:
__________
Answer:
By knowing the values below 1 km can help you to find how far above or below Park Headquarters a given point of interest is located
Question 22.
b. How can you find the number of points of interest that are less than 1 km above or below Park Headquarters?
Type below:
__________
Answer:
By counting the number of points of interest that are less than 1 km, you can find the number of points of interest that are less than 1 km above or below Park Headquarters.
Question 22.
c. Find how far above or below Park Headquarters each point of interest is located.
Type below:
__________
Answer:
C, D, E, F, G, H
Question 22.
d. How many points of interest are less than 1 kilometer above or below Park Headquarters?
Type below:
__________
Answer:
6
Question 23.
Use Reasoning Name a rational number that can replace ? to make both statements true.
?>−3 |?|<|−3|
Type below:
__________
Answer:
-2 or -1 >−3 1 or 2 < |−3|
Explanation:
The greatest numbers than -3 are -2 or -1.
|−3| = 3. So, the fewer numbers than 3 are 1, 2
Question 24.
Laila said |4| equals |−4|. Is Laila correct? Use the number line and words to support your answer.
Type below:
__________
Answer:
Laila is correct. The absolute value of |−4| = 4 = |4|
Absolute Value – Page No. 169
Find the absolute value.
Question 1.
|7|
Type below:
__________
Answer:
7
Explanation:
The distance from 0 to the point I graphed is 2 units.
|7| = 7
Question 2.
|−8|
Type below:
__________
Answer:
8
Explanation:
The distance from 0 to the point I graphed is 2 units.
|−8| = 8
Question 3.
|16|
Type below:
__________
Answer:
16
Explanation:
The distance from 0 to the point I graphed is 2 units.
|16| = 16
Question 4.
|8.65|
Type below:
__________
Answer:
8.65
Explanation:
The distance from 0 to the point I graphed is 2 units.
|8.65| = 8.65
Question 5.
|4\(\frac{3}{20}\)|
Type below:
__________
Answer:
4\(\frac{3}{20}\)
Explanation:
The distance from 0 to the point I graphed is 2 units.
|4\(\frac{3}{20}\)| = 4\(\frac{3}{20}\)
Question 6.
|−5000|
Type below:
__________
Answer:
5000
Explanation:
The distance from 0 to the point I graphed is 2 units.
|−5000| = 5000
Find all numbers with the given absolute value.
Question 7.
12
Type below:
__________
Answer:
12 and -12
Explanation:
12 and -12 are at the same distance from 0.
Question 8.
1.7
Type below:
__________
Answer:
1.7 and -1.7
Explanation:
1.7 and -1.7 are at the same distance from 0.
Question 9.
\(\frac{3}{5}\)
Type below:
__________
Answer:
\(\frac{3}{5}\) and \(\frac{-3}{5}\)
Explanation:
\(\frac{3}{5}\) and \(\frac{-3}{5}\) are at the same distance from 0.
Question 10.
3\(\frac{1}{6}\)
Type below:
__________
Answer:
3\(\frac{1}{6}\) and -3\(\frac{1}{6}\)
Explanation:
3\(\frac{1}{6}\) and -3\(\frac{1}{6}\) are at the same distance from 0.
Question 11.
0
Type below:
__________
Answer:
0
Explanation:
0 is same distance from 0.
Find the number or numbers that make the statement true.
Question 12.
|?| = 17
Type below:
__________
Answer:
17 and -17
Explanation:
|-17| = 17
|17| = 17
Question 13.
|?| = 2.04
Type below:
__________
Answer:
2.04 and -2.04
Explanation:
|-2.04| = 2.04
|2.04| = 2.04
Question 14.
|?| = 1\(\frac{9}{10}\)
Type below:
__________
Answer:
1\(\frac{9}{10}\) and -1\(\frac{9}{10}\)
Explanation:
|-1\(\frac{9}{10}\)| = 1\(\frac{9}{10}\)
|1\(\frac{9}{10}\)| = 1\(\frac{9}{10}\)
Question 15.
|?| = \(\frac{19}{24}\)
Type below:
__________
Answer:
\(\frac{19}{24}\) and \(\frac{-19}{24}\)
Explanation:
|\(\frac{-19}{24}\)| = \(\frac{19}{24}\)
|\(\frac{19}{24}\)| = \(\frac{19}{24}\)
Problem Solving
Question 16.
Which two numbers are 7.5 units away from 0 on a number line?
Type below:
__________
Answer:
7.5 and -7.5 are away from 0 on a number line
Explanation:
|7.5| = 7.5
|-7.5| = 7.5
Question 17.
Emilio is playing a game. He just answered a question incorrectly, so his score will change by −10 points. Find the absolute value of −10.
Type below:
__________
Answer:
10
Explanation:
Emilio is playing a game. He just answered a question incorrectly, so his score will change by −10 points.
|-10| = 10
Question 18.
Write two different real-world examples. One should involve the absolute value of a positive number, and the other should involve the absolute value of a negative number.
Type below:
__________
Answer:
1) If we have a balance of -$35 dollars in an account, we may also choose to represent that as a debt of $35.
2) The temperature of the human body
Lesson Check – Page No. 170
Question 1.
What is the absolute value of \(\frac{8}{9}\)?
Type below:
__________
Answer:
\(\frac{8}{9}\)
Explanation:
|\(\frac{8}{9}\)| = \(\frac{8}{9}\)
Question 2.
What two numbers have an absolute value of 21.63?
Type below:
__________
Answer:
21.63 and -21.63
Explanation:
|-21.63| = 21.63
|21.63| = 21.63
Spiral Review
Question 3.
Rachel earned $89.70 on Tuesday. She spent $55.89 at the grocery store. How much money does she have left?
$ ______
Answer:
$33.81
Explanation:
Rachel earned $89.70 on Tuesday. She spent $55.89 at the grocery store.
89.70 – 55.89 = 33.81
Rachel has $33.81 left
Question 4.
One carton contains \(\frac{17}{20}\) liter of juice. Another carton contains 0.87 liter of juice. Which carton contains the most?
Type below:
__________
Answer:
0.87 is more because 17/20 is 0.85
Explanation:
One carton contains \(\frac{17}{20}\) liter of juice. Another carton contains 0.87 liters of juice.
0.87 is more because 17/20 is 0.85
Question 5.
Maggie jogged \(\frac{7}{8}\) mile on Monday and \(\frac{1}{2}\) of that distance on Tuesday. How far did she jog on Tuesday?
\(\frac{□}{□}\) mile
Answer:
\(\frac{7}{4}\) mile
Explanation:
Maggie jogged \(\frac{7}{8}\) mile on Monday and \(\frac{1}{2}\) of that distance on Tuesday.
\(\frac{7}{8}\) ÷ \(\frac{1}{2}\) = 7/4
7/4 or as a mixed fraction which is 1 3/4 mile
Question 6.
Trygg has \(\frac{3}{4}\) package of marigold seeds. He plants \(\frac{1}{6}\) of those seeds in his garden and divides the rest equally into 10 flowerpots. What fraction of a package of seeds is planted in each flowerpot?
\(\frac{□}{□}\) package
Answer:
\(\frac{1}{16}\) package
Explanation:
He has a 3/4 package and plants 1/6 of the seeds.
3/4 × 1/6 = 1/8
He divides the rest equally into 10 flowerpots.
Subtract 1/8 from 3/4.
The common denominator of 4 and 8 is 8.
Multiply the numerator 3 × 2= 6 with a denominator of 8.
3/4 – 1/8 = 6/8 -1/8 = 5/8
5/8 is left to be divided equally into 10 flowerpots.
5/8 ÷ 10/1
= 5/8 * 1/10
= 5/80
= 1/16
Share and Show – Page No. 173
Question 1.
On Monday, Allie’s bank account balance was – $24. On Tuesday, her account balance was less than it was on Monday. Use absolute value to describe Allie’s balance on Tuesday as a debt.
Type below:
__________
Answer:
On Tuesday, her account balance is less than -$24 means her debt will be bigger than $24 dollars.
Explanation:
On Monday, allies’ bank account balance was -$24.
Balance being negative means he is carrying a debt of $24.
On Tuesday, Allie’s balance account was less than it was on Monday. It means
Her bank account < -$24
So, she must be carrying a debit bigger than $24.
Therefore, on Tuesday, her account balance being less than -$24 means her debt will be greater than $24 dollars.
Question 2.
Matthew scored −36 points in his turn at a video game. In Genevieve’s turn, she scored fewer points than Matthew. Use absolute value to describe Genevieve’s score as a loss.
Type below:
__________
Answer:
Genevieve lost more than 36 points
Explanation:
Matthew scored −36 points in his turn at a video game. In Genevieve’s turn, she scored fewer points than Matthew.
-36 > -40
|-36| < |-40|
36 < 40
Genevieve lost more than 36 points
On Your Own
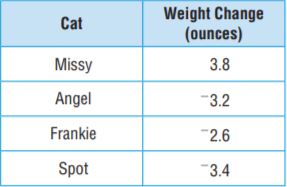
Question 3.
One of the cats shown in the table is a tabby. The tabby had a decrease in weight of more than 3.3 ounces. Which cat is the tabby?
Type below:
__________
Answer:
Spot is tabby
Explanation:
|-3.4| = 3.4
So, Spot is tabby
Compare. Write <, >, or =.
Question 4.
−8 _____ |−8|
Answer:
−8 < |−8|
Explanation:
|−8| = 8
-8 < 8
Question 5.
13 _____ |−13|
Answer:
13 = |−13|
Explanation:
|−13| = 13
13 = 13
Question 6.
|−23| _____ |−24|
Answer:
|−23| < |−24|
Explanation:
|−23| = 23
|−24| = 24
23 < 24
Question 7.
15 _____ |−14|
Answer:
15 > |−14|
Explanation:
|−14| = 14
15 > 14
Question 8.
34 _____ |−36|
Answer:
34 < |−36|
Explanation:
|−36| = 36
34 < 36
Question 9.
−5 _____ |−6|
Answer:
−5 < |−6|
Explanation:
|−6| = 6
-5 < 6
Question 10.
Write the values in order from least to greatest.

Type below:
__________
Answer:
1, 2, 3, 6
Explanation:
|-2| = 2
|3| = 3
|-6| = 6
|1| = 1
1 < 2 < 3 < 6
Compare and Contrast – Page No. 174
When you compare and contrast, you look for ways that two or more subjects are alike (compare) and ways they are different (contrast). This helps you to discover information about each subject that you might not have known otherwise. As you read the following passage, think about how the main topics are alike and how they are different.
Trevor mows lawns after school to raise money for a new mountain bike. Last week, it rained every day, and he couldn’t work. While waiting for better weather, he spent some of his savings on lawnmower repairs. As a result, his savings balance changed by −$45. This week, the weather was better, and Trevor returned to work. His savings balance changed by +$45 this week.
Question 11.
The passage has two main parts. Describe them.
Type below:
__________
Answer:
Last week, Trevor couldn’t work, so he spent money to repair the lawnmower!
This week, he goes back to work and earns money again!
Question 12.
Describe the two changes in Trevor’s savings balance
Type below:
__________
Answer:
His savings balance changed by −$45 in one week and his savings balance changed by +$45 in another week.
Question 13.
Reason Quantitatively Compare the two changes in Trevor’s savings balance. How are they alike?
Type below:
__________
Answer:
Each week, Trevor’s balance changed by $45; or his balance is the same distance from 0 each week.
Question 14.
Contrast the two changes in Trevor’s savings balance. How are they different?
Type below:
__________
Answer:
The balances are different because one week the balance had a decrease, while the next week there was an increase in the balance
Compare Absolute Values – Page No. 175
Solve.
Question 1.
Jamie scored −5 points on her turn at a trivia game. In Veronica’s turn, she scored more points than Jamie. Use absolute value to describe Veronica’s score as a loss.
Type below:
__________
Jamie scored −5 points on her turn at a trivia game. In Veronica’s turn, she scored more points than Jamie.
Answer:
In this situation, |-5| represents a loss of 5 points. Veronica lost fewer than 5 points.
Question 2.
The low temperature on Friday was −10°F. The low temperature on Saturday was colder. Use absolute value to describe the temperature on Saturday as a temperature below zero.
Type below:
__________
Answer:
The temperature on Sunday was more than 10 degrees below zero
Explanation:
The low temperature on Friday was −10°F. The low temperature on Saturday was colder. The temperature on Sunday was more than 10 degrees below zero
Question 3.
The table shows changes in the savings accounts of five students. Which student had the greatest increase in money? By how much did the student’s account increase?
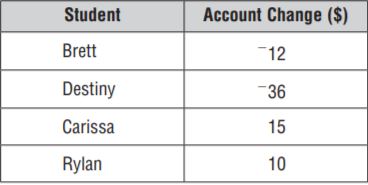
Type below:
__________
Answer:
Carissa; an increase of $15
Compare. Write <, >, or =.
Question 4.
−16 _____ |−16|
Answer:
−16 < |−16|
Explanation:
|−16| = 16
-16 < 16
Question 5.
20 _____ 20
Answer:
20 = 20
Question 6.
3 _____ |−4|
Answer:
3 < |−4|
Explanation:
|−4| = 4
3 < 4
Problem Solving
Question 7.
On Wednesday, Miguel’s bank account balance was −$55. On Thursday, his balance was less than that. Use absolute value to describe Miguel’s balance on Thursday as a debt.
Type below:
__________
Answer:
In this situation, -$55 represents a debt of $55. On Thursday, Miguel had a debt of more than $55.
Explanation:
On Wednesday, Miguel’s bank account balance was −$55. On Thursday, his balance was less than that.
In this situation, -$55 represents a debt of $55. On Thursday, Miguel had a debt of more than $55.
Question 8.
During a game, Naomi lost points. She lost fewer than 3 points. Use an integer to describe her possible score.
Type below:
__________
Answer:
-2, -1
Explanation:
During a game, Naomi lost points. She lost fewer than 3 points.
It may be -2, -1
Question 9.
Give two numbers that fit this description: a number is less than another number but has a greater absolute value. Describe how you determined the numbers.
Type below:
__________
Answer:
Choose a large negative number and a smaller positive number.
Example: Use -14 and 3, -8392 and 274, -1 and 0.5, etc. Even though the negative numbers are technically less, they would have higher absolute values.
Lesson Check – Page No. 176
Question 1.
A temperature of –6° is colder than a temperature of 5°F below zero. Is this statement true or false?
Type below:
__________
Answer:
True
Explanation:
–6° is colder than a temperature of 5°F below zero
Question 2.
Long Beach, California has an elevation of −7 feet. New Orleans, Louisiana is 8 feet below sea level. Which city has a lower elevation?
Type below:
__________
Answer:
New Orleans, Louisiana has a lower elevation
Explanation:
Long Beach, California has an elevation of −7 feet.
New Orleans, Louisiana is 8 feet below sea level. = -8 feet
So, New Orleans, Louisiana has a lower elevation.
Spiral Review
Question 3.
Dawn and Lin took off on skateboards from the same location but traveled in opposite directions. After 20 minutes, Dawn had traveled 6.42 kilometers and Lin had traveled 7.7 kilometers. How far apart were they?
_____ kilometers
Answer:
14.12 kilometers
Explanation:
Distance of Dawn = 6.42 km
Distance from Lin = 7.7 km in the opposite direction.
If they went in opposite directions then they were moving away from each other.
The final distance between the two, d = 6.42 + 7.7 = 14.12 km
After 20 minutes Dawn and Lin were 14.12 km away.
Question 4.
Rico and Josh took off on skateboards going in the same direction. After 20 minutes, Rico had traveled 5.98 kilometers and Josh had gone 8.2 kilometers. How far apart were they?
_____ kilometers
Answer:
2.22 kilometers
Explanation:
Rico and Josh took off on skateboards going in the same direction.
After 20 minutes, Rico had traveled 5.98 kilometers and Josh had gone 8.2 kilometers.
D = 8.2 – 5.98 = 2.22 km
Hence, Rico and Josh were 2.22 km apart from each other.
Question 5.
Etta bought 11.5 yards of fabric selling for $0.90 per yard. What was the total cost?
$ _____
Answer:
$10.35
Explanation:
Multiply 11.5 times 0.90 and get $10.35
Question 6.
Yen calculates the product \(\frac{5}{8} \times \frac{24}{25}\). Before he multiplies, he simplifies all factors. What does the problem look like after he simplifies the factors?
Type below:
__________
Answer:
Yen calculates the product \(\frac{5}{8} \times \frac{24}{25}\).
5/8 = 0.625
24/25 = 0.96
0.625 × 0.96 = 0.6
Share and Show – Page No. 179
Question 1.
Write the ordered pair for point J.
Type below:
__________
Answer:
(-1.5, 2.5)
Explanation:
To find the x-coordinate, move 1.5 units to the left.
To find the y-coordinate, move 2.5 units up.
Point J is located at (-1.5, 2.5)
Write the ordered pair for the point.
Question 2.
K
Type below:
__________
Answer:
(1, -1.5)
Explanation:
To find the x-coordinate, move 1 unit to the right.
To find the y-coordinate, move 1.5 units down.
Point K is located at (1, -1.5)
Question 3.
L
Type below:
__________
Answer:
(-2, -1.75)
Explanation:
To find the x-coordinate, move 2 units to the left.
To find y-coordinate, move 1.75 units down.
Point L is located at (-2, -1.75)
Question 4.
M
Type below:
__________
Answer:
(1, 0)
Explanation:
To find the x-coordinate, move 1 unit to the right.
To find y-coordinate, move 0 units.
Point M is located at (1, 0)
Graph and label the point on the coordinate plane.
Question 5.
P(-2.5, 2)
Type below:
__________
Answer:
The x-coordinate is negative. Move 2.5 units to the left.
y-coordinate is positive. Move 2 units up
Question 6.
Q(-2, \(\frac{1}{4}\))
Type below:
__________
Answer:
The x-coordinate is negative. Move 2 units to the left.
y-coordinate is positive. Move 0.25 units up
Question 7.
R(0, 1.5)
Type below:
__________
Answer:
The x-coordinate is positive. Move 0 units.
y-coordinate is positive. Move 1.5 units up
Question 8.
S(-1, \(\frac{-1}{2}\))
Type below:
__________
Answer:
The x-coordinate is negative. Move 1 unit to the left.
y-coordinate is negative. Move 0.5 units down
Question 9.
T( 1\(\frac{1}{2}\), -2 )
Type below:
__________
Answer:
The x-coordinate is positive. Move 1.5 units to the right.
y-coordinate is negative. Move 2 units down
Question 10.
U(0.75, 1.25)
Type below:
__________
Answer:
The x-coordinate is positive. Move 0.75 units to the right.
y-coordinate is positive. Move 1.25 units up
Question 11.
V(-0.5, 0)
Type below:
__________
Answer:
The x-coordinate is negative. Move 0.5 units to the left.
y-coordinate is positive. Move 0 units
Question 12.
W(2, 0)
Type below:
__________
Answer:
The x-coordinate is positive. Move 2 units to the right.
y-coordinate is positive. Move 0 units up
Question 13.
X(0, -2)
Type below:
__________
Answer:
The x-coordinate is positive. Move 0 units.
y-coordinate is negative. Move 2 units down
On Your Own
Write the ordered pair for the point. Give approximate coordinates when necessary.
Question 14.
A
Type below:
__________
Answer:
(4, 4)
Explanation:
To find the x-coordinate, move 4 units to the right.
To find y-coordinate, move 4 units up.
Point A is located at (4, 4)
Question 15.
B
Type below:
__________
Answer:
(-4, 3)
Explanation:
To find the x-coordinate, move 4 units to the left.
To find y-coordinate, move 3 units up.
Point B is located at (-4, 3)
Question 16.
C
Type below:
__________
Answer:
(-3, 1)
Explanation:
To find the x-coordinate, move 3 units to the left.
To find y-coordinate, move 1 unit up.
Point C is located at (-3, 1)
Question 17.
D
Type below:
__________
Answer:
(-2, -3)
Explanation:
To find the x-coordinate, move 2 units to the left.
To find y-coordinate, move 3 units down.
Point D is located at (-2, -3)
Question 18.
E
Type below:
__________
Answer:
(5, -3)
Explanation:
To find the x-coordinate, move 5 units to the right.
To find y-coordinate, move 3 units down.
Point E is located at (5, -3)
Question 19.
F
Type below:
__________
Answer:
(2.5, 0)
Explanation:
To find the x-coordinate, move 2.5 units to the right.
To find y-coordinate, move 0 units.
Point F is located at (2.5, 0)
Question 20.
G
Type below:
__________
Answer:
(-4, -5)
Explanation:
To find the x-coordinate, move 4 units to the left.
To find y-coordinate, move 5 units down.
Point G is located at (-4, -5)
Question 21.
H
Type below:
__________
Answer:
(0, 3.5)
Explanation:
To find the x-coordinate, move 0 units.
To find y-coordinate, move 3.5 units up.
Point H is located at (0, 3.5)
Question 22.
J
Type below:
__________
Answer:
(0.5, 0.5)
Explanation:
To find the x-coordinate, move 0.5 units to the right.
To find y-coordinate, move 0.5 units up.
Point J is located at (0.5, 0.5)
Graph and label the point on the coordinate plane.
Question 23.
M(-4, 0)
Type below:
__________
Answer:
The x-coordinate is negative. Move 4 units to the left.
y-coordinate is positive. Move 0 units
Question 24.
N(2, 2)
Type below:
__________
Answer:
The x-coordinate is positive. Move 2 units to the right.
y-coordinate is positive. Move 2 units up
Question 25.
P(-3, 3)
Type below:
__________
Answer:
The x-coordinate is positive. Move 3 units to the left.
y-coordinate is positive. Move 3 units up
Question 26.
Q(0, −2\(\frac{1}{2}\))
Type below:
__________
Answer:
The x-coordinate is positive. Move 0 units.
y-coordinate is negative. Move 2.5 units down
Explanation:
Question 27.
R(0.5, 0.5)
Type below:
__________
Answer:
The x-coordinate is positive. Move 0.5 units to the right.
y-coordinate is positive. Move 0.5 units up
Question 28.
S(-5, \(\frac{1}{2}\))
Type below:
__________
Answer:
The x-coordinate is negative. Move 5 units to the left.
y-coordinate is positive. Move 0.5 units up
Question 29.
T(0, 0)
Type below:
__________
Answer:
It is at the origin. T is at the origin
Question 30.
U(3 \(\frac{1}{2}\), 0)
Type below:
__________
Answer:
The x-coordinate is positive. Move 3.5 units to the right.
y-coordinate is positive. Move 0 units
Question 31.
V(-2, -4)
Type below:
__________
Answer:
The x-coordinate is negative. Move 2 units to the left.
y-coordinate is negative. Move 4 units down
Question 32.
Look for Structure A point lies to the left of the y-axis and below the x-axis. What can you conclude about the coordinates of the point?
Type below:
__________
Answer:
A point lies to the left of the y-axis. So, the x-coordinate is negative.
A point lies below the x-axis. So, y-coordinate is negative.
Both coordinates points are negative
Problem Solving + Applications – Page No. 180
Many of the streets in downtown Philadelphia can be modeled by a coordinate plane, as shown on the map. Each unit on the map represents one block. Use the map for 33 and 34.
Question 33.
Anita works at the Historical Society. She leaves the building and walks 3 blocks north to a restaurant. What ordered pair represents the restaurant?
Type below:
__________
Answer:
Anita works at the Historical Society. She leaves the building and walks 3 blocks north to a restaurant.
Historical Society = (2, 4)
As she walks 3 blocks north to a restaurant 4-3 = 1
(2, 1) ordered pair represents the restaurant
Question 34.
Pose a Problem Write and solve a new problem that uses a location on the map.
Type below:
__________
Answer:
Anita is at City Hall. She walked 3 blocks to the East and 2 blocks to the North. What ordered pair represents her present location?
She is at the Fabric Workshop & Museum. The ordered pair is (3, 2)
Question 35.
The points A, B, C, and D on a coordinate plane can be connected to form a rectangle. Point A is located at (2, 0), point B is located at (6, 0), and point C is located at (6, –2.5). Write the ordered pair for point D.
Type below:
__________
Answer:
The point D is at (2, -2.5)
Explanation:
The points A, B, C, and D on a coordinate plane can be connected to form a rectangle. Point A is located at (2, 0), point B is located at (6, 0), and point C is located at (6, –2.5). The point D is at (2, -2.5)
Question 36.
Identify Relationships Explain how you can tell that the line segment connecting two points is vertical without graphing the points.
Type below:
__________
Answer:
The line segment connecting two points is vertical. By calculating the slope, we can say that the line segment connecting two points is vertical without graphing the points.
Question 37.
For numbers 37a–37d, select True or False for each statement.
37a. Point A (2, –1) is to the right of the y-axis and below the x-axis.
37b. Point B (– 5,2) is to the left of the y-axis and below the x-axis.
37c. Point C (3, 2) is to the right of the y-axis and above the x-axis.
37d. Point D (–2, –1) is to the left of the y-axis and below the x-axis.
37a. __________
37b. __________
37c. __________
37d. __________
Answer:
37a. True
37b. False
37c. True
37d. True
Rational Numbers and the Coordinate Plane – Page No. 181
Write the ordered pair for the point. Give approximate coordinates when necessary.
Question 1.
A
Type below:
__________
Answer:
(1, 0.5)
Explanation:
To find the x-coordinate, move 1 unit to the right.
To find y-coordinate, move 0.5 units up.
Point A is located at (1, 0.5)
Question 2.
B
Type below:
__________
Answer:
(-0.75, -2.5)
Explanation:
To find the x-coordinate, move 0.75 units to the left.
To find y-coordinate, move 2.5 units down.
Point B is located at (-0.75, -2.5)
Question 3.
C
Type below:
__________
Answer:
(2, -1.5)
Explanation:
To find the x-coordinate, move 2 units to the right.
To find y-coordinate, move 1.5 units down.
Point C is located at (2, -1.5)
Question 4.
D
Type below:
__________
Answer:
(-1.5, 0)
Explanation:
To find the x-coordinate, move 1.5 units to the left.
To find y-coordinate, move 0 units.
Point D is located at (-1.5, 0)
Graph and label the point on the coordinate plane.
Question 5.
G(−\(\frac{1}{2}\), 1 \(\frac{1}{2}\))
Type below:
__________
Answer:
The x-coordinate is negative. Move 0.5 units to the left.
y-coordinate is positive. Move 1.5 units up
Explanation:
-1/2 = -0.5
1 1/2 = 3/2 = 1.5
Question 6.
H(0, 2.50)
Type below:
__________
Answer:
The x-coordinate is positive. Move 0 units.
y-coordinate is positive. Move 2.5 units up
Question 7.
J(−1 \(\frac{1}{2}\), \(\frac{1}{2}\))
Type below:
__________
Answer:
The x-coordinate is negative. Move 1.5 units to the left.
y-coordinate is positive. Move 0.5 units up
Explanation:
-1 1/2 = -3/2 = -1.5
1/2 = 0.5
Question 8.
K(1, 2)
Type below:
__________
Answer:
The x-coordinate is positive. Move 1 unit to the right.
y-coordinate is positive. Move 2 units up
Question 9.
L(−1 \(\frac{1}{2}\), −2 \(\frac{1}{2}\))
Type below:
__________
Answer:
The x-coordinate is negative. Move 1.5 units to the left.
y-coordinate is negative. Move 2.5 units down
Explanation:
-1 1/2 = -3/2 = -1.5
-2 1/2 = -5/2 = -2.5
Question 10.
M(1, -0.5)
Type below:
__________
Answer:
The x-coordinate is positive. Move 1 unit to the up.
y-coordinate is negative. Move 0.5 units down
Question 11.
N(\(\frac{1}{4}\), 1 \(\frac{1}{2}\))
Type below:
__________
Answer:
The x-coordinate is positive. Move 0.25 units to the right.
y-coordinate is positive. Move 1.5 units up
Question 12.
P(1.25, 0)
Type below:
__________
Answer:
The x-coordinate is positive. Move 1.25 units to the right.
y-coordinate is positive. Move 0 units
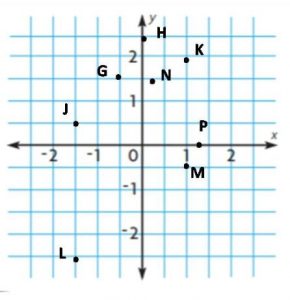
Problem Solving
Use the map for 13–15.
Question 13.
What is the ordered pair for the city hall?
Type below:
__________
Answer:
(-1, 0.5)
Explanation:
To find the x-coordinate, move 1 unit to the left.
To find y-coordinate, move 0.5 units up.
City Hall is located at (-1, 0.5)
Question 14.
The post office is located at (\(\frac{−1}{2}\), 2). Graph and label a point on the map to represent the post office.
Type below:
__________
Answer:
Explanation:
The x-coordinate is negative. Move 0.5 units to the left.
y-coordinate is positive. Move 2 units up
Question 15.
Describe how to graph the ordered pair (−1, 4.5).
Type below:
__________
Answer:
The x-coordinate is negative. Move 1 unit to the left.
y-coordinate is positive. Move 4.5 units up
Lesson Check – Page No. 182
Question 1.
An artist uses a coordinate plane to create a design. As part of the design, the artist wants to graph the point (−6.5, 2). How should the artist graph this point?
Type below:
__________
Answer:
The Artist should go 6.5 units to the left on the x-axis and then 2 units up on the y-axis giving:
graph {((x + 6.5)^2 + (y – 2)^2 – 0.0125) = 0 [-10, 5, -5, 2.5]}
Question 2.
What are the coordinates of the campground?
Type below:
__________
Answer:
(-1, -1.5)
Explanation:
The x-coordinate is negative. Move 1 unit to the left.
y-coordinate is negative. Move 1.5 units down
Spiral Review
Question 3.
Four students volunteer at the hospital. Casey volunteers 20.7 hours, Danielle 20 \(\frac{3}{4}\) hours, Javier 18 \(\frac{9}{10}\) hours, and Forrest, 20 \(\frac{18}{25}\) hours. Who volunteered the greatest number of hours?
__________
Answer:
Danielle volunteered the greatest number of hours
Explanation:
Danielle volunteered the most. She did 20.75 hours while Forest had 20.72, Casey had 20.7 and Javier had the least at 18.90 hours.
Question 4.
Directions for making a quilt say to cut fifteen squares with sides that are 3.625 inches long. What is the side length written as a fraction?
_____ \(\frac{□}{□}\)
Answer:
3\(\frac{5}{8}\)
Explanation:
3.625 = 3 0.625
3.625 = 3 0.625(1000)/1000
3.625 = 3 625/1000
3.625 = 3 (625/125) / (1000/125)
3.625 = 3 5/8
The decimal length of the side of the squares (3.625 inches long) witten as a fraction is 3 5/8 inches long.
Question 5.
Cam has a piece of plywood that is 6 \(\frac{7}{8}\) feet wide. He is going to cut shelves from the plywood that are each 1 \(\frac{1}{6}\) feet wide. Which is a good estimate for the number of shelves Cam can make?
Type below:
__________
Answer:
5 shelves
Explanation:
6 7/8= 55/8
6 1/6= 7/6
first, find common denominators
55/8 × 3= 165/24
7/6 × 4= 28/24
165/24 divided by 28/24 is the same as 165/24 time 24/28
so that equals 3960/672 = 5.8928
About 5 shelves
Question 6.
Zach has \(\frac{3}{4}\) hour to play video games. It takes him \(\frac{1}{12}\) hour to set up the system. Each round of his favorite game takes \(\frac{1}{6}\) hour. How many rounds can he play?
_____ rounds
Answer:
4 rounds
Explanation:
Zach has 3/4 hour to play video games. it takes him 1/12 hour to set up the system. Each round of his favorite game takes 1/6 hours.
1) Zach has 3/4 hour to play video games
Convert to minutes
1 hour = 60 minutes
3/4 × 60 = 45 minutes
2) It takes him an hour to set up the system
Convert to minutes
1/12 × 60 = 5 minutes
3) 45 minutes – 5 minutes = 40 minutes
4) Each round of his favorite game takes an hour
Convert to minutes
1/6 × 60 = 10 minutes
5) Divide the time available to play video games by the time each round of his favorite game
40/10 = 4 rounds
Share and Show – Page No. 185
Identify the quadrant where the point is located.
Question 1.
(2, -5)
Type below:
__________
Answer:
Quadrant IV
Explanation:
The x-coordinate is positive. So, the point is 2 units to the right of the origin.
Since the point is to the right of the origin, it must be located in either
Quadrant I or Quadrant IV
The y-coordinate is negative, so the point is 5 units down from the origin.
Since the point is down the origin, it must be located in Quadrant IV.
Check by graphing the point (2, -5) on the coordinate plane.
Quadrant IV.
Question 2.
(4, 1)
Type below:
__________
Answer:
Quadrant I
Explanation:
The x-coordinate is positive. So, the point is 4 units to the right of the origin.
Since the point is to the right of the origin, it must be located in either
Quadrant I or Quadrant IV
y-coordinate is positive, so the point is 1 unit up from the origin.
Since the point is up to the origin, it must be located in Quadrant I.
Check by graphing the point (4, 1) on the coordinate plane.
Quadrant I.
Question 3.
(-6, -2)
Type below:
__________
Answer:
Quadrant III
Explanation:
The x-coordinate is negative. So, the point is 6 units to the left of the origin.
Since the point is to the left of the origin, it must be located in either
Quadrant II or Quadrant III
The y-coordinate is negative, so the point is 2 units down from the origin.
Since the point is down the origin, it must be located in Quadrant III.
Quadrant III.
Question 4.
(-7, 3)
Type below:
__________
Answer:
Quadrant II
Explanation:
The x-coordinate is negative. So, the point is 7 units to the left of the origin.
Since the point is to the left of the origin, it must be located in either
Quadrant II or Quadrant III
The y-coordinate is positive, so the point is 3 units up from the origin.
Since the point is up to the origin, it must be located in Quadrant II.
Quadrant II.
Question 5.
(8, 8)
Type below:
__________
Answer:
Quadrant I
Explanation:
The x-coordinate is positive. So, the point is 8 units to the right of the origin.
Since the point is to the right of the origin, it must be located in either
Quadrant I or Quadrant IV
The y-coordinate is positive, so the point is 8 units up from the origin.
Since the point is up to the origin, it must be located in Quadrant I.
Quadrant I.
Question 6.
(1, -1)
Type below:
__________
Answer:
Quadrant IV
Explanation:
The x-coordinate is positive. So, the point is 1 unit to the right of the origin.
Since the point is to the right of the origin, it must be located in either
Quadrant I or Quadrant IV
The y-coordinate is negative, so the point is 1 unit down from the origin.
Since the point is down to the origin, it must be located in Quadrant IV.
Quadrant IV.
The two points are reflections of each other across the x- or y-axis. Identify the axis.
Question 7.
(-1, 3) and (1, 3)
Type below:
__________
Answer:
y-axis
Explanation:
The given x-axis points are -1 and 1
The y-axis points are 3 and 3
The y-axis points are reflections to each other
Question 8.
(4, 4) and (4, -4)
Type below:
__________
Answer:
x-axis
Explanation:
The given x-axis points are 4 and 4
The y-axis points are 4 and -4
The x-axis points are reflections to each other
Question 9.
(2, -9) and (2, 9)
Type below:
__________
Answer:
x-axis
Explanation:
The given x-axis points are 2 and 2
The y-axis points are -9 and 9
The x-axis points are reflections to each other
Question 10.
(8, 1) and (-8, 1)
Type below:
__________
Answer:
y-axis
Explanation:
The given x-axis points are 8 and -8
The y-axis points are 1 and 1
The y-axis points are reflections to each other
On Your Own
Identify the quadrant where the point is located.
Question 11.
(-8, -9)
Type below:
__________
Answer:
Quadrant III
Explanation:
The x-coordinate is negative. So, the point is 8 units to the left of the origin.
Since the point is to the left of the origin, it must be located in either
Quadrant II or Quadrant III
The y-coordinate is negative, so the point is 9 units down from the origin.
Since the point is down to the origin, it must be located in Quadrant III.
Quadrant III.
Question 12.
(12, 1)
Type below:
__________
Answer:
Quadrant I
Explanation:
The x-coordinate is positive. So, the point is 12 units to the right of the origin.
Since the point is to the right of the origin, it must be located in either
Quadrant I or Quadrant IV
The y-coordinate is positive, so the point is 1 unit up from the origin.
Since the point is up to the origin, it must be located in Quadrant I.
Quadrant I.
Question 13.
(-13, 10)
Type below:
__________
Answer:
Quadrant II
Explanation:
The x-coordinate is negative. So, the point is 13 units to the left of the origin. Since the point is to the left of the origin, it must be located in either
Quadrant II or Quadrant III
The y-coordinate is negative, so the point is 10 units up from the origin.
Since the point is up to the origin, it must be located in Quadrant II.
Quadrant II.
Question 14.
(5, -20)
Type below:
__________
Answer:
Quadrant IV
Explanation:
The x-coordinate is positive. So, the point is 5 units to the right of the origin.
Since the point is to the right of the origin, it must be located in either
Quadrant I or Quadrant IV
The y-coordinate is negative, so the point is 20 units down from the origin.
Since the point is down to the origin, it must be located in Quadrant IV.
Quadrant IV.
The two points are reflections of each other across the x- or y-axis. Identify the axis.
Question 15.
(-9, -10) and (-9, 10)
Type below:
__________
Answer:
x-axis
Explanation:
The given x-axis points are -9 and -9
The y-axis points are -10 and 10
The x-axis points are reflections to each other
Question 16.
(21, -31) and (21, 31)
Type below:
__________
Answer:
x-axis
Explanation:
The given x-axis points are 21 and 21
The y-axis points are -31 and 31
The x-axis points are reflections to each other
Question 17.
(15, -20) and (-15, -20)
Type below:
__________
Answer:
y-axis
Explanation:
The given x-axis points are 15 and -15
The y-axis points are -20 and -20
The y-axis points are reflections to each other
Give the reflection of the point across the given axis.
Question 18.
(−7, −7), y-axis
Type below:
__________
Answer:
(7, -7)
Explanation:
The x-axis point is -7.
So, the reflection of point 7
Question 19.
(−15, 18), x-axis
Type below:
__________
Answer:
(-15, -18)
Explanation:
The y-axis point is 18.
So, the reflection of a point -18
Question 20.
(11, 9), x-axis
Type below:
__________
Answer:
(11, -9)
Explanation:
The y-axis point is 9.
So, the reflection of a point -9
Problem Solving + Applications – Page No. 186
Use the map of Gridville for 21–23.
Question 21.
The library’s location has opposite x- and y-coordinates as City Hall. Across which streets could you reflect City Hall’s location to find the library’s location?
Type below:
__________
Answer:
The library’s location has opposite x- and y-coordinates as City Hall.
City Hall = (2, -3)
The opposite x- and y-coordinates of City Hall = (-2, 3)
So, the library’s location is (-2, 3)
Question 22.
Each unit on the map represents 1 mile. Gregory leaves his house at (−5, 4), cycles 4 miles east, 6 miles south, and 1 mile west. In which quadrant of the city is he now?
Type below:
__________
Answer:
Quadrant III
Explanation:
Gregory leaves his house at (−5, 4)
cycles 4 miles east = -5 + 4 = -1; (-1, 4)
6 miles south = (-1, -1)
1 mile west (-2, -1)
So, he is now in Quadrant III
Question 23.
The bus station has the same x-coordinate as City Hall but the opposite y-coordinate. In which quadrant of the city is the bus station located?
Type below:
__________
Answer:
Quadrant I
Explanation:
The bus station has the same x-coordinate as City Hall but the opposite y-coordinate.
City Hall = (2, -3)
The opposite y-coordinate = 3
Bus station located at (2, 3)
Bus station located at Quadrant I
Question 24.
Describe Relationships Describe the relationship between the locations of the points (2, 5) and (2, −5) on the coordinate plane.
Type below:
__________
Answer:
(2, 5) and (2, −5) have the same x-coordinate.
They have the opposite y-coordinate.
Question 25.
Identify the quadrant where each point is located. Write each point in the correct box.
(−1, 3), (4, −2), (−3, −2), (1, −3), (−1, 2), (3, 4)
Type below:
__________
Answer:
(−1, 3) = Quadrant II
(4, −2) = Quadrant IV
(−3, −2) = Quadrant III
(1, −3) = Quadrant IV
(−1, 2) = Quadrant II
(3, 4) = Quadrant I
Problem Solving + Applications – Page No. 187
Identify the quadrant where the point is located.
Question 1.
(10, -2)
Type below:
__________
Answer:
Quadrant IV
Explanation:
The x-coordinate is positive. So, the point is 10 units to the right of the origin.
Since the point is to the right of the origin, it must be located in either
Quadrant I or Quadrant IV
The y-coordinate is negative, so the point is 2 units down from the origin.
Since the point is down the origin, it must be located in Quadrant IV.
Quadrant IV
Question 2.
(-5, -6)
Type below:
__________
Answer:
Quadrant III
Explanation:
The x-coordinate is negative. So, the point is 5 units to the left of the origin.
Since the point is to the left of the origin, it must be located in either
Quadrant II or Quadrant III
The y-coordinate is negative, so the point is 6 units down from the origin.
Since the point is down the origin, it must be located in Quadrant III.
Quadrant III.
Question 3.
(3, 7)
Type below:
__________
Answer:
Quadrant I
Explanation:
The x-coordinate is positive. So, the point is 3 units to the right of the origin.
Since the point is to the right of the origin, it must be located in either
Quadrant I or Quadrant IV
y-coordinate is positive, so the point is 7 units up from the origin.
Since the point is up to the origin, it must be located in Quadrant I.
Quadrant I
The two points are reflections of each other across the x- or y-axis. Identify the axis.
Question 4.
(5, 3) and (−5, 3)
Type below:
__________
Answer:
y-axis
Explanation:
The given x-axis points are 5 and -5
The y-axis points are 3 and 3
The y-axis points are reflections to each other
Question 5.
(−7, 1) and (−7, −1)
Type below:
__________
Answer:
x-axis
Explanation:
The given x-axis points are -7 and -7
The y-axis points are 1 and -1
The x-axis points are reflections to each other
Question 6.
(−2, 4) and (−2, −4)
Type below:
__________
Answer:
x-axis
Explanation:
The given x-axis points are -2 and -2
The y-axis points are 4 and -4
The x-axis points are reflections to each other
Give the reflection of the point across the given axis.
Question 7.
(−6, −10), y-axis
Type below:
__________
Answer:
(6, -10)
Explanation:
The x-axis point is -6.
So, the reflection of the point 6
Question 8.
(−11, 3), x-axis
Type below:
__________
Answer:
(-11, -3)
Explanation:
The y-axis point is -3.
So, the reflection of a point 3
Question 9.
(8, 2), x-axis
Type below:
__________
Answer:
(8, -2)
Explanation:
The y-axis point is 2.
So, the reflection of a point -2
Problem Solving
Question 10 .
A town’s post office is located at the point (7, 5) on a coordinate plane. In which quadrant is the post office located?
Type below:
__________
Answer:
Quadrant I
Explanation:
A town’s post office is located at the point (7, 5) on a coordinate plane.
The x-coordinate is positive. So, the point is 7 units to the right of the origin.
Since the point is to the right of the origin, it must be located in either
Quadrant I or Quadrant IV
The y-coordinate is positive, so the point is 5 units up from the origin.
Since the point is up the origin, it must be located in Quadrant I.
Quadrant I
Question 11.
The grocery store is located at a point on a coordinate plane with the same y-coordinate as the bank but with the opposite x-coordinate. The grocery store and bank are reflections of each other across which axis?
Type below:
__________
Answer:
y-axis
Explanation:
The grocery store is located at a point on a coordinate plane with the same y-coordinate as the bank but with the opposite x-coordinate.
The grocery store and bank are reflections of each other across the y-axis.
Question 12.
Explain to a new student how a reflection across the y-axis changes the coordinates of the original point.
Type below:
__________
Answer:
The coordinate plane with the same y-coordinate remains same but with the opposite x-coordinate.
Lesson Check – Page No. 188
Question 1.
In which quadrant does the point (−4, 15) lie?
Type below:
__________
Answer:
Quadrant II
Explanation:
The x-coordinate is negative. So, the point is 4 units to the left of the origin.
Since the point is to the left of the origin, it must be located in either
Quadrant II or Quadrant III
The y-coordinate is positive, so the point is 15 units up from the origin.
Since the point is up to the origin, it must be located in Quadrant II.
Quadrant II.
Question 2.
What are the coordinates of the point (10, −4) if it is reflected across the y–axis?
Type below:
__________
Answer:
(-10, -4)
Explanation:
coordinates of the point (-10, −4)
If it is reflected across the y–axis, coordinates of the point will be (-10, -4)
Spiral Review
Question 3.
Small juice bottles come in packages of 6. Yogurt treats come in packages of 10. Paula wants to have the exact same number of each item. What is the least number of bottles of juice and individual yogurt treats she will have? How many packages of each will she need?
Type below:
__________
Answer:
5 packages
Explanation:
Number of packages of small juice bottles = 6
Number of packages of yogurt = 10
For this, we will find the L.C.M. of 6 and 10 =30
So, there will be 5 packages of small juice bottles and 3 packages of yogurt.
Question 4.
Alison saves $29.26 each month. How many months will it take her to save enough money to buy a stereo for $339.12?
_____ month
Answer:
11 months
Explanation:
Round 29 and 339 to 30 and 340.
Divide 340 by 30
The answer should be 11.3 repeatings.
11 months
Question 5.
The library is 1.75 miles directly north of the school. The park is 0.6 miles directly south of the school. How far is the library from the park?
Type below:
__________
Answer:
2.35 miles
Explanation:
The library is 1.75 miles directly north of the school. The park is 0.6 miles directly south of the school.
1.75 + 0.6 would be 2.35 miles, the library to the parking.
Question 6.
Tours of the art museum are offered every \(\frac{1}{3}\) hour starting at 10 A.M. The museum closes at 4:00 P.M. How many tours are offered each day?
_____ tours
Answer:
18 tours
Explanation:
Staring time of tours=10 am
Closing time of tours=4 pm
Duration of tours(10 am to 4 pm)=6 hours
Time for each tour= 1/3 hours
Total number of tours offered in a day= 6 × 3 = 18
Therefore, 18 tours offered each day.
Share and Show – Page No. 191
Find the distance between the pair of points.
Question 1.
(−3, 1) and (2, 1)
_____ units
Answer:
5 units
Explanation:
The points have the same y-coordinate, so they are located on a horizontal line.
Find the distance between the x-coordinates of the point (-3, 1) and the point (2, 1)
|-3| = 3
3 + 2 = 5
Question 2.
(2, 1) and (2, -4)
_____ units
Answer:
5 units
Explanation:
The points have the same x-coordinate, so they are located on a vertical line.
Find the distance between the y-coordinates of the point (2, 1) and the point (2, -4)
|-4| = 4
1 + 4 = 5
Question 3.
(2, -4) and (4, -4)
_____ units
Answer:
2 units
Explanation:
The points have the same y-coordinate, so they are located on a horizontal line.
Find the distance between the x-coordinates of the point (2, -4) and the point (4, -4)
4 – 2 = 2
Question 4.
(-3, 3) and (-3, 1)
_____ units
Answer:
2 units
Explanation:
The points have the same x-coordinate, so they are located on a vertical line.
Find the distance between the y-coordinates of the point (-3, 3) and the point (-3, 1)
3 – 1 = 2
On Your Own
Practice: Copy and Solve Graph the pair of points. Then find the distance between them.
Question 5.
(0, 5) and (0, -5)
_____ units
Answer:
10 units
Explanation:
The points have the same x-coordinate, so they are located on a vertical line.
Find the distance between the y-coordinates of the point (0, 5) and the point (0, -5)
|-5| = 5
5 + 5 = 10
Question 6.
(1, 1) and (1, -3)
_____ units
Answer:
4 units
Explanation:
The points have the same x-coordinate, so they are located on a vertical line.
Find the distance between the y-coordinates of the point (1, 1) and the point (1, -3)
|-3| = 3
1 + 3 = 4
Question 7.
(-2, -5) and (-2, -1)
_____ units
Answer:
4 units
Explanation:
The points have the same x-coordinate, so they are located on a vertical line.
Find the distance between the y-coordinates of the point (-2, -5) and the point (-2, -1)
|-5| = 5
|-1| = 1
5 – 1 = 4
Question 8.
(-7, 3) and (5, 3)
_____ units
Answer:
12 units
Explanation:
The points have the same y-coordinate, so they are located on a horizontal line.
Find the distance between the x-coordinates of the point (-7, 3) and the point (5, 3)
|-7| = 7
7 + 5 = 12
Question 9.
(3, -6) and (3, -10)
_____ units
Answer:
4 units
Explanation:
The points have the same x-coordinate, so they are located on a vertical line.
Find the distance between the y-coordinates of the point (3, -6) and the point (3, -10)
|-6| = 6
|-10| = 10
10 – 6 = 4
Question 10.
(8, 0) and (8, -8)
_____ units
Answer:
8 units
Explanation:
The points have the same x-coordinate, so they are located on a vertical line.
Find the distance between the y-coordinates of the point (8, 0) and the point (8, -8)
|-8| = 8
0 + 8 = 8
Use Reasoning Algebra Write the coordinates of a point that is the given distance from the given point.
Question 11.
4 units from (3, 5)
Type below:
__________
Answer:
1 or 9
Explanation:
4 units from (3, 5)
(3, 9) or (3, 1)
Question 12.
6 units from (2, 1)
Type below:
__________
Answer:
8 or -4
Explanation:
6 units from (2, 1)
(8, 1) or (-4, 1)
Question 13.
7 units from (−4, −1)
Type below:
__________
Answer:
-8 or 6
Explanation:
7 units from (−4, −1)
(-8, -1) or (-8, 6)
Problem Solving + Applications – Page No. 192
An archaeologist is digging at an ancient city. The map shows the locations of several important finds. Each unit represents 1 kilometer. Use the map for 14–18.
Question 14.
How far is it from the stadium to the statue?
_____ km
Answer:
8 km
Explanation:
Stadium = (4, 5)
statue = (4, -3)
The points have the same x-coordinate, so they are located on a vertical line.
Find the distance between the y-coordinates of the point (4, 5) and the point (4, -3)
|-3| = 3
5 + 3 = 8
Question 15.
The archaeologist drives 3 km south from the palace. How far is he from the market?
_____ km
Answer:
3 km
Explanation:
The palace is at the origin (0, 0)
So, the answer is 3 km
Question 16.
The archaeologist’s campsite is located at (−9, −3). How far is it from the campsite to the market?
_____ km
Answer:
11 km
Explanation:
the campsite is located at (−9, −3)
the market is located at (-2, -3)
The points have the same y-coordinate, so they are located on a horizontal line.
Find the distance between the x-coordinates of the point (−9, −3) and the point (-2, -3)
|-9| = 9
|-2| = 2
9 + 2 = 11
campsite is 11 km far to the market
Question 17.
The archaeologist rode east on a donkey from the Great Gate, at (−11, 4), to the Royal Road. Then he rode south to the palace. How far did the archaeologist ride?
_____ km
Answer:
15 km
Explanation:
The archaeologist rode east on a donkey from the Great Gate, at (−11, 4), to the Royal Road. Then he rode south to the palace.
First, he needs to move |-11| = 11 km
Then, he needs to move 4 km
4 + 11 = 15 km
Question 18.
Generalize Explain how you could find the distance from the palace to any point on the Imperial Highway.
Type below:
__________
Answer:
The distance varies according to the points on the Imperial Highway
Question 19.
Select the pairs of points that have a distance of 10 between them. Mark all that apply.
(3, −6) and (3, 4)
( −3, 8) and (7, 8)
(4, 5) and (6, 5)
(4, 1) and (4, 11)
Type below:
__________
Answer:
(3, −6) and (3, 4)
( −3, 8) and (7, 8)
(4, 5) and (6, 5)
Explanation:
6 + 4 = 10
3 + 7 = 10
4 + 6 = 10
Distance on the Coordinate Plane – Page No. 193
Find the distance between the pair of points.
Question 1.
(1, 4) and (−3, 4)
_____ units
Answer:
4 units
Explanation:
The points have the same y-coordinate, so they are located on a horizontal line.
Find the distance between the x-coordinates of the point (1, 4) and the point (−3, 4)
|-3| = 3
1 + 3 = 4
Question 2.
(7, −2) and (11, −2)
_____ units
Answer:
3 units
Explanation:
The points have the same y-coordinate, so they are located on a horizontal line.
Find the distance between the x-coordinates of the point (7, −2) and the point (11, −2)
11 – 7 = 3
Question 3.
(6, 4) and (6, −8)
_____ units
Answer:
12 units
Explanation:
The points have the same x-coordinate, so they are located on a vertical line.
Find the distance between the y-coordinates of the point (6, 4) and the point (6, −8)
|-8| = 8
4 + 8 = 12
Question 4.
(8, −10) and (5, −10)
_____ units
Answer:
3 units
Explanation:
The points have the same y-coordinate, so they are located on a horizontal line.
Find the distance between the x-coordinates of the point (8, −10) and the point (5, −10)
8 – 5 = 3
Question 5.
(−2, −6) and (−2, 5)
_____ units
Answer:
11 units
Explanation:
The points have the same x-coordinate, so they are located on a vertical line.
Find the distance between the y-coordinates of the point (−2, −6)and the point (−2, 5)
|-6| = 6
6 + 5 = 11
Question 6.
(−5, 2) and (−5, −4)
_____ units
Answer:
6 units
Explanation:
The points have the same x-coordinate, so they are located on a vertical line.
Find the distance between the y-coordinates of the point (−5, 2) and the point (−5, −4)
|-4| = 4
2 + 4 = 6
Write the coordinates of a point that is the given distance from the given point.
Question 7.
5 units from (−1, −2)
Type below:
__________
Answer:
-6 or 4
Explanation:
5 units from (−1, −2)
(-6, -2) or (4, -2)
Question 8.
8 units from (2, 4)
Type below:
__________
Answer:
12 or -4
Explanation:
8 units from (2, 4)
(2, 12) or (2, -4)
Question 9.
3 units from (−7, −5)
Type below:
__________
Answer:
-2 or -8
Explanation:
3 units from (−7, −5)
(-7, -2) or (-7, -8)
Problem Solving
The map shows the locations of several areas in an amusement park. Each unit represents 1 kilometer.
Question 10.
How far is the Ferris wheel from the rollercoaster?
_____ km
Answer:
4 km
Explanation:
Ferris wheel = (5, 6)
rollercoaster = (5, 2)
6 – 2 = 4
Question 11.
How far is the water slide from the restrooms?
_____ km
Answer:
7 km
Explanation:
water slide = (-3, -4)
restrooms = (4, -4)
3 + 4 = 7
Question 12.
Graph the points (23, 3), (23, 7), and (4, 3) on a coordinate plane. Explain how to find the distance from (23, 3) to (23, 7) and from (23, 3) and (4, 3).
Type below:
__________
Answer:
Explanation:
(23, 3) to (23, 7)
The points have the same x-coordinate, so they are located on a vertical line.
Find the distance between the y-coordinates of the point (23, 3) and the point (23, 7)
7 – 3 = 4
(23, 3) and (4, 3).
The points have the same y-coordinate, so they are located on a horizontal line.
Find the distance between the x-coordinates of the point (23, 3) and the point (4, 3)
4 – 3 = 1
Lesson Check – Page No. 194
Question 1.
What is the distance between (4, −7) and (−5, −7)?
_____ units
Answer:
9 units
Explanation:
(4, −7) and (−5, −7)
The points have the same y-coordinate, so they are located on a horizontal line.
Find the distance between the x-coordinates of the point (4, −7) and the point (−5, −7)
|-5| = 5
5 + 4 = 9
Question 2.
Point A and point B are 5 units apart. The coordinates of point A are (3, −9). The y–coordinate of point B is −9. What is a possible x–coordinate for point B?
Type below:
__________
Answer:
8 or -2
Explanation:
Point A and point B are 5 units apart. The coordinates of point A are (3, −9). The y–coordinate of point B is −9.
The points have the same y-coordinate, so they are located on a horizontal line.
the distance between the x-coordinates = 5
So, 8 or -2
Spiral Review
Question 3.
An apple is cut into 10 pieces. 0.8 of the apple is eaten. Which fraction, in simplest form, represents the amount of apple that is left?
\(\frac{□}{□}\)
Answer:
\(\frac{1}{5}\)
Explanation:
An apple is cut into 10 pieces. 0.8 of the apple is eaten.
10/10 – 8/10 = 2/10 = 1/5 amount of apple left.
Question 4.
A carton contains soup cans weighing a total of 20 pounds. Each can weighs 1 \(\frac{1}{4}\) pounds. How many cans does the carton contain?
_____ cans
Answer:
16 cans
Explanation:
Divide 20 with 5/4 (=1 1/4)
So, 20 × 4/5 which would be 80/5 = 16 cans
Question 5.
List −1, \(\frac{1}{4}\), and −1 \(\frac{2}{3}\) in order from greatest to least.
Type below:
__________
Answer:
\(\frac{1}{4}\), -1, −1 \(\frac{2}{3}\)
Explanation:
\(\frac{1}{4}\) > -1 > −1 \(\frac{2}{3}\)
Question 6.
The point located at (3, −1) is reflected across the y−axis. What are the coordinates of the reflected point?
Type below:
__________
Answer:
(-3, -1)
Explanation:
The point located at (3, −1) is reflected across the y−axis.
(-3, -1)
Share and Show – Page No. 197
Question 1.
Busby County is rectangular. A map of the county on a coordinate plane shows the vertices of the county at (−5, 8), (8, 8), (8, −10), and (−5, −10). Each unit on the map represents 1 mile. What is the county’s perimeter?
_____ miles
Answer:
62 miles
Explanation:
Busby County is rectangular. A map of the county on a coordinate plane shows the vertices of the county at (−5, 8), (8, 8), (8, −10), and (−5, −10).
The distance of (−5, 8) is 8
The distance of (8, 8) is 8
The distance between -5 to 8 is 5 + 8 = 13
The distance of (8, −10) is 10
The distance of (−5, −10) is 10
The distance between -5 to 8 is 5 + 8 = 13
8 + 8 + 13 + 10 + 10 + 13 = 62
Question 2.
What if the vertices of the county were (−5, 8), (8, 8), (8, −6), and (−5, −6)? What would the perimeter of the county be?
_____ miles
Answer:
54 miles
Explanation:
The distance from – 5 to 8 is 5 + 8 = 13
The distance from – 5 to 8 is 5 + 8 = 13
The distance from 8 to -6 is 8 + 6 = 14
The distance from 8 to -6 is 8 + 6 = 14
13 + 14 + 13 + 14 = 54
Question 3.
On a coordinate map of Melville, a restaurant is located at (−9, −5). A laundry business is located 3 units to the left of the restaurant on the map. What are the map coordinates of the laundry business?
Type below:
__________
Answer:
(-12, -5)
Explanation:
On a coordinate map of Melville, a restaurant is located at (−9, −5).
A laundry business is located 3 units to the left of the restaurant on the map.(-12, -5) is the answer
Question 4.
The library is 4 blocks north and 9 blocks east of the school. The museum is 9 blocks east and 11 blocks south of the school. How far is it from the library to the museum?
_____ blocks
Answer:
15 blocks
Explanation:
the library is 4 blocks north = (0, 4)
9 blocks east = (9, 4)
The museum is 9 blocks east = (9, 0)
11 blocks south = (9, -11)
4 + 11 = 15
Problem Solving + Applications – Page No. 198
Question 5.
Make Sense of Problems Diana left her campsite at (2, 6) on a map of Big Trees Park, hiked to Redwood Grove at (−5, 6), and continued on to Bass Lake at (−5, −3). Each unit on the map represents 1 kilometer. How far did Diana hike?
_____ km
Answer:
16 km
Explanation:
Diana left her campsite at (2, 6) on a map of Big Trees Park, hiked to Redwood Grove at (−5, 6), 2 + 5 = 7
and continued on to Bass Lake at (−5, −3), 6 + 3 = 9
7 + 9 = 16 km
Question 6.
Hector left his house at (−6, 13) on a map of Coleville and walked to the zoo at (−6, 2). From there he walked east to his friend’s house. He walked a total distance of 25 blocks. If each unit on the map represents one block, what are the coordinates of Hector’s friend’s house?
Type below:
__________
Answer:
(19,2) should be the answer. He was -6 above the x-axis. Going east for 25 unit means he walked horizontally keeping the y-axis same
Question 7.
In November, the price of a cell phone was double the price in March. In December, the price was $57, which was $29 less than the price in November. What was the price of the cell phone in March?
$ _____
Answer:
$172
Explanation:
In November, the price of a cell phone was double the price in March. In December, the price was $57, which was $29 less than the price in November.
29 + 57 = 86
86 × 2 = $172
Question 8.
A map of the city holding the Olympics is placed on a coordinate plane. Olympic Stadium is located at the origin of the map. Each unit on the map represents 2 miles.
Graph the locations of four other Olympic buildings.
Max said the distance between the Aquatics Center and the Olympic Village is greater than the distance between the Media Center and the Basketball Arena. Do you agree with Max? Use words and numbers to support your answer
Type below:
__________
Answer:
Max said is correct
Aquatics Center = (8, 4)
Olympic Village = (-8, 4)
The distance = 8 + 8 = 16
Media Center = (4, -5)
Basketball Arena = (-8, -5)
The distance = 4 + 8 = 12
Problem Solving The Coordinate Plane – Page No. 199
Read each problem and solve.
Question 1.
On a coordinate map of Clifton, an electronics store is located at (6, −7). A convenience store is located 7 units north of the electronics store on the map. What are the map coordinates of the convenience store?
Type below:
__________
Answer:
(6, 0)
Explanation:
On a coordinate map of Clifton, an electronics store is located at (6, −7). A convenience store is located 7 units north of the electronics store on the map.
The map coordinates of the convenience store is (6, 0)
Question 2.
Sonya and Lucas walk from the school to the library. They walk 5 blocks south and 4 blocks west to get to the library. If the school is located at a point (9, −1) on a coordinate map, what are the map coordinates of the library?
Type below:
__________
Answer:
(5, -6)
Explanation:
The school is at (9, −1)
5 blocks South mean that you subtract 5 from the y coordinate:
(9, -1-5) = (9, -6)
4 blocks West means that you subtract 4 from the x coordinate:
(9-4, -6) = (5, -6)
The library is at (5, -6)
Question 3.
On a coordinate map, Sherry’s house is at the point (10, −2) and the mall is at point (−4, −2). If each unit on the map represents one block, what is the distance between Sherry’s house and the mall?
_____ blocks
Answer:
14 blocks
Explanation:
(10,-2)
(-4,-2)
x value- 10-(-4)=14
y value- Since both y values are the same, you don’t do anything.
Question 4.
Arthur left his job at (5, 4) on a coordinate map and walked to his house at (5, −6). Each unit on the map represents 1 block. How far did Arthur walk?
_____ blocks
Answer:
10 blocks
Explanation:
He walked 10 blocks. 4 to -6 is 10. 4, 3, 2, 1, 0, -1, -2, -3, -4, -5, -6.
Question 5.
A fire station is located 2 units east and 6 units north of a hospital. If the hospital is located at a point (−2, −3) on a coordinate map, what are the coordinates of the fire station?
Type below:
__________
Answer:
(0, 3)
Explanation:
the hospital is located at a point (−2, −3).
A fire station is located 2 units east and 6 units north of a hospital.
(-2 +2, -3+6) = (0,3)
Question 6.
Xavier’s house is located at the point (4, 6). Michael’s house is 10 blocks west and 2 blocks south of Xavier’s house. What are the coordinates of Michael’s house?
Type below:
__________
Answer:
(-6, 4)
Explanation:
the coordinates are -6,4. (x-10,y-2)
Question 7.
Write a problem that can be solved by drawing a diagram on a coordinate plane.
Type below:
__________
Answer:
On a coordinate map, Sherry’s house is at the point (10, −2) and the mall is at point (−4, −2). If each unit on the map represents one block, what is the distance between Sherry’s house and the mall?
Lesson Check – Page No. 200
Question 1.
The points (−4, −4), (−4, 4), (4, 4), and (4, −4) form a square on a coordinate plane. How long is a side length of the square?
_____ units
Answer:
8 units
Explanation:
-4 + 4 = 8 units
side length of the square is 8 units
Question 2.
On a coordinate map, the museum is located at (−5, 7). A park is located 6 units to the right of the museum on the map. What are the coordinates of the park?
Type below:
__________
Answer:
(1, 7)
Explanation:
On a coordinate map, the museum is located at (−5, 7). A park is located 6 units to the right of the museum on the map.
(1,7)
Spiral Review
Question 3.
On a grid Joe’s house is marked at (−5, −3) and Andy’s house is marked at (1, −3). What is the distance, on the grid, between Joe’s house and Andy’s house?
_____ units
Answer:
6 units
Explanation:
On a grid Joe’s house is marked at (−5, −3) and Andy’s house is marked at (1, −3).
|-5| = 5
5 + 0 = 5
0 + 1 = 1
5 + 1 = 6
Question 4.
In the last two years, Mari grew 2 \(\frac{1}{4}\) inches, Kim grew 2.4 inches, and Kate grew 2 \(\frac{1}{8}\) inches. Write the amounts they grew in order from least to greatest.
Type below:
__________
Answer:
2 \(\frac{1}{8}\), 2 \(\frac{1}{4}\), 2.4
Explanation:
In the last two years, Mari grew 2 \(\frac{1}{4}\) inches, Kim grew 2.4 inches, and Kate grew 2 \(\frac{1}{8}\) inches.
2 \(\frac{1}{4}\) = 9/4 = 2.25
2 \(\frac{1}{8}\) = 17/8 = 2.125
2.125, 2.25, 2.4
Question 5.
A jar of jelly that weighs 4.25 ounces costs $2.89. What is the cost of one ounce of jelly?
$ _____
Answer:
$0.68
Explanation:
A jar of jelly that weighs 4.25 ounces costs $2.89.
$2.89/4.25 = $0.68
Question 6.
Jan began with \(\frac{5}{6}\) pound of modeling clay. She used \(\frac{1}{5}\) of the clay to make decorative magnets. She divided the remaining clay into 8 equal portions. What is the weight of the clay in each portion?
\(\frac{□}{□}\) pounds
Answer:
\(\frac{1}{12}\) pounds
Explanation:
Weight of modelling clay is = 5/6 pounds
Part of clay used to make decorative magnets is = 1/5
Remaining part of clay = 1 – 1/5 = 4/5
So, Remaining part of clay is divided into 8 equal parts so, Weight of each clay is given by 4/5 × 5/6 × 1/8 = 1/12 pounds
So, weight of the clay in each portion is 1/12 pounds
Chapter 3 Review/Test – Page No. 201
Question 1.
For numbers 1a–1d, choose Yes or No to indicate whether the situation can be represented by a negative number.
1a. Sherri lost 100 points answering a question wrong. Yes No
1b. The peak of a mountain is 2,000 feet above sea level. Yes No
1c. Yong paid $25 for a parking ticket. Yes No
1d. A puppy gained 3 pounds. Yes No
1a. __________
1b. __________
1c. __________
1d. __________
Answer:
1a. Yes
1b. No
1c. No
1d. No
Question 2.
The low weekday temperatures for a city are shown.
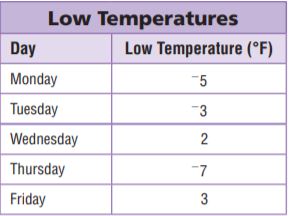
Part A
Using the information in the table, order the temperatures from lowest to highest.
Type below:
__________
Answer:
-7, -5, -3, 2, 3
Explanation:
Monday = -5
Tuesday = -3
Wednesday = 2
Thursday = -7
Friday = 3
-7, -5, -3, 2, 3
Question 2.
Part B
Explain how to use a vertical number line to determine the order.
Type below:
__________
Answer:
Place the -3, -5, -7, are below the 0. And place 2 and 3 are above the 0.
Page No. 202
Question 3.
For numbers 3a–3e, choose Yes or No to indicate whether the number is between –1 and –2.
3a. \(\frac{-4}{5}\) Yes No
3b. 1 \(\frac{2}{3}\) Yes No
3c. −1.3 Yes No
3d. −1 \(\frac{1}{4}\) Yes No
3e. −2 \(\frac{1}{10}\) Yes No
3a. __________
3b. __________
3c. __________
3d. __________
3e. __________
Answer:
3a. No
3b. No
3c. Yes
3d. Yes
3e. No
Explanation:
3a. \(\frac{-4}{5}\) = -0.8
3b. 1 \(\frac{2}{3}\) = 1.666
3c. -1.3
3d. −1 \(\frac{1}{4}\) = -1.25
3e. −2 \(\frac{1}{10}\) = -21/10 = -2.1
Question 4.
Compare \(\frac{-1}{5}\) and –0.9. Use numbers and words to explain your answer
Type below:
__________
Answer:
\(\frac{-1}{5}\) = -0.2
-0.9
-0.2 and -0.9 both are negative numbers. They lies between 0 and -1
Question 5.
Jeandre said |3| equals |–3|. Is Jeandre correct? Use a number line and words to support your answer.
Type below:
__________
Answer:
Explanation:
Yes, he is correct and he is referring to the absolute values of number 3 and -3. And by absolute value, this is the distance of the number from the origin zero (0) which is symbolized by two vertical lines, as |3| or |-3| is equal to 3.
The picture shows a number line where green is the origin zero (0). The purple line is the distance between 0 and 3 which is 3. The pink one is the distance of -3 from 0 which is also 3. Therefore, |3| equals |-3|
Question 6.
Write the values in order from least to greatest.

Type below:
__________
Answer:
|2| |-4| |8| |-12|
Explanation:
|-4| = 4
|2| = 2
|-12| = 12
|8| = 8
2, 4, 8, 12
Question 7.
For numbers 7a–7d, select True or False for each statement.
7a. The x-coordinate of any point on the y-axis is 0. True False
7b. Point D(–2, 1) is to the left of the y-axis and below the x-axis. True False
7c. The point where the axes intersect is the origin. True False
7d. If both the x- and y- coordinates are positive, the point is to the right of the y-axis and below the x-axis. True False
__________
__________
__________
__________
Answer:
7a. True
7b. False
7c. True
7d. False
Page No. 203
Question 8.
Mia’s house is located at point (3, 4) on a coordinate plane. The location of Keisha’s house is the reflection of the location of Mia’s house across the y-axis. In what quadrant is Keisha’s house in?
Type below:
__________
Answer:
quadrant II
Explanation:
Mia’s house is located at point (3, 4) on a coordinate plane. The location of Keisha’s house is the reflection of the location of Mia’s house across the y-axis.
quadrant II is the answer.
Question 9.
Points A(3, 8) and B(–4, 8) are located on a coordinate plane. Graph the pair of points. Then find the distance between them. Use numbers and words to explain your answer.
Type below:
__________
Answer:
Explanation:
Points A(3, 8) and B(–4, 8) are located on a coordinate plane.
3 + 0 = 3
|-4| = 4
4 + 0 = 4
3 + 4 = 7
7 units
Page No. 204
Question 10.
The map shows the location J of Jose’s house and the location F of the football field. Jose is going to go to Tyrell’s house and then the two of them are going to go to the football field for practice.
Part A
Tyrell’s house is located at point T, the reflection of point J across the y-axis. What are the coordinates of points T, J, and F?
Type below:
__________
Answer:
coordinates of points T (6, 8)
coordinates of points J (-6, 8), and
coordinates of points F(-5, 6)
Question 10.
Part B
If each unit on the map represents 1 block, what was the distance Tyrell traveled to the football field and what was the distance Jose traveled to the football field? Use numbers and words to explain your answer
Type below:
__________
Answer:
If each unit on the map represents 1 block, the distance Jose traveled to the football field
coordinates of points T (6, 8)
coordinates of points J (-6, 8)
|-6| = 6
6 + 6 = 12 units.
the distance Tyrell traveled to the football field
coordinates of points T (6, 8)
coordinates of points F(-5, 6)
6 + 5 = 11 units
Question 11.
For numbers 11a–11d, choose Yes or No to indicate whether the situation could be represented by the integer +3.
11a. A football team gains 3 yards on a play. Yes No
11b. A golfer’s score is 3 over par. Yes No
11c. A student answers a Yes No 3-point question correctly. Yes No
11d. A cat loses 3 pounds. Yes No
11a. __________
11b. __________
11c. __________
11d. __________
Answer:
11a. Yes
11b. Yes
11c. Yes
11d. No
Page No. 205
Question 12.
Jason used a map to record the elevations of five locations.
Jason wrote the elevations in order from lowest to highest : -3, 5, 8 -18, -20.
Is Jason correct? Use words and numbers to explain why or why not. If Jason is incorrect, what is the correct order?
Type below:
__________
Answer:
Jason is incorrect.
the elevations in order from lowest to highest: -20, -18, -3, 5, 8
Question 13.
For numbers 13a–13d, select True or False for each statement.
13a. \(\frac{1}{5}\) is between 0 and 1. True False
13b. −2 \(\frac{2}{3}\) is between -1 and -2. True False
13c. −3 \(\frac{5}{8}\) is between -3 and -4. True False
13d. 4 \(\frac{3}{4}\) is between 3 and 4. True False
13a. __________
13b. __________
13c. __________
13d. __________
Answer:
13a. True
13b. False
13c. True
13d. False
Question 14.
Choose <, >, or =.
14a. 0.25 ο \(\frac{3}{4}\)
14b. 2 \(\frac{7}{8}\) ο 2.875
14c. \(\frac{1}{3}\) ο 0.325
14d. \(\frac{-3}{4}\) ο \(\frac{-1}{2}\)
0.25 ____ \(\frac{3}{4}\)
2 \(\frac{7}{8}\) _____ 2.875
\(\frac{1}{3}\) _____ 0.325
\(\frac{-3}{4}\) _____ \(\frac{-1}{2}\)
Answer:
0.25 < \(\frac{3}{4}\)
2 \(\frac{7}{8}\) = 2.875
\(\frac{1}{3}\) > 0.325
\(\frac{-3}{4}\) < \(\frac{-1}{2}\)
Explanation:
\(\frac{3}{4}\) = 0.75
0.25 < \(\frac{3}{4}\)
2 \(\frac{7}{8}\) = 23/8 = 2.875
2 \(\frac{7}{8}\) = 2.875
\(\frac{-3}{4}\) = -0.75
\(\frac{-1}{2}\) = -0.5
Page No. 206
Question 15.
Graph 4 and −4 on the number line.
Tyler says both 4 and −4 have an absolute value of 4. Is Tyler correct? Use the number line and words to explain why or why not.
Type below:__________
Answer:
Tyler is correct.
|-4| = 4
|4| = 4
Question 16.
Lindsay and Will have online accounts for buying music. Lindsay’s account balance is −$20 and Will’s account balance is −$15. Express each account balance as a debt and explain whose debt is greater.
Type below:
__________
Answer:
Lindsey is 5$ more in dept than Will.
Lindsey= -20$
Will= -15$
Question 17.
Explain how to graph points A(–3, 0), B(0, 0), and C(0, –3) on the coordinate plane. Then, explain how to graph point D, so that ABCD is a square.
Type below:
__________
Answer:
First place the points A(–3, 0), B(0, 0), and C(0, –3) on the coordinate plane.
The length from point A to point B is 3.
A square has equal lengths on each side.
So, to find D, Add 3 units to the left to C or down to A.
D(-3, -3)
Question 18.
Point A(2, –3) is reflected across the x-axis to point B. Point B is reflected across the y-axis to point C. What are the coordinates of point C? Use words and numbers to explain your answer.
Type below:
__________
Answer:
Quadrant III
Explanation:
Point A(2, –3) is reflected across the x-axis to point B. Point B is reflected across the y-axis to point C.
So, Point B is (2,3)
Point C is (-2, 3)
C is in Quadrant III
Conclusion:
We believe that the details provided in the HMH Go Math 6th Grade Answer Key for Chapter 3 Understand Positive and Negative Numbers made you happy. All the explanations are prepared by the math experts as per the latest syllabus. Compare the questions in real-time so that you can understand concepts easily. Stay with us to get the answer keys for all the chapters of grade 6.
Bank Nifty Pivot Point Calculator has both positive and negative values in it.
Must Read:
CE3391 – Fluid Mechanics and Machinery Syllabus Regulation 2021 Anna University
