Want to know what the Parallel Lines are? Then you are on the correct page and you will get the complete knowledge of Parallel Lines. Parallel lines are part of geometry, if students are aware of these lines they can easily construct any type of line in 5th Grade Math Concepts. Lines are of indefinite length and we all know that ladder has many steps but they never meet each other like parallel lines. Let’s dive into this guide and study Parallel Lines & their properties with some examples in detail.
Do Check:
What are Parallel Lines?
In geometry, parallel lines can be defined as the two lines at equal distance on the same plane and never intersect each other, and the distance between the two parallel lines remains constant. Parallel lines are also known as non-intersecting lines. We can say parallel lines meet at infinity. If we have two lines A and B of the same length and parallel and equidistant to each other then we say A is parallel to B. Let us see how the parallel lines look as follows
Parallel Lines – Definition
If two given lines do not intersect each other at any point in a plane and always keep the same distance between them called parallel lines. Also, the lines never cross paths with each other are parallel lines. To represent or to denote parallel lines between two lines we use the symbol ‘ || ‘. Angles are formed when two parallel lines cut transversal.
For example, to represent two line segments AB and CD as \(\overline{AB}\)||\(\overline{CD}\), and read as the line segment \(\overline{AB}\) is parallel to \(\overline{CD}\). The distance between the two lines is constant.

Conditions of Parallelism
Parallel lines maybe two or more. To know the lines given are parallel, kids should be aware of the following points:
- Lines do not have any common point in between in a plane.
- Lines have to be on the same plane.
- Distance between the lines always remains constant throughout.
- Parallel lines may be straight, vertical, diagonal, and horizontal.
Properties of Parallel Lines
The following are the properties of lines that are parallel:
- The corresponding angles of the parallel lines are equal.
- The vertically opposite angles are equal.
- The alternate interior and exterior angles of the parallel lines are equal.
- The lines that are parallel at a given point are parallel to each other.
- The pair of interior angles on the similar side of the transversal is supplementary.
For more detailed information on the Properties of Parallel Lines, click here.
Parallel Lines Theorems
Kids who are excited to learn the theorems of parallel lines can have a look at the following points:
- If two lines intersect each other, then the vertically opposite angles are equal.
- In case a transversal meets two parallel lines, then each pair of alternate interior angles is equal.
- In case a transversal intersects two parallel lines, then each pair of interior angles on the same side of the transversal is supplementary.
- If a transversal meets two lines such that a pair of alternate interior angles is equal, then the two lines are parallel.
- If a transversal intersects two lines so that a pair of interior angles on the same side of the transversal is supplementary, then the two lines are parallel.
Parallel Lines Equation
If two lines are parallel to each other in a plane, then the slopes of both lines are to be equal. Consider m1 and m2 are the slopes of two lines.
Parallel lines = m1 = m2
To find the parallel line with slope m and which is passing through a point ( x1, y1) then the following formula is used.
Slope = -a/b
Parallel lines equation is y-y1 = m(x-x1)
Parallel Lines Examples
Example 1:
If two lines m || n and ∠a=25o, what will be the measure of ∠b?
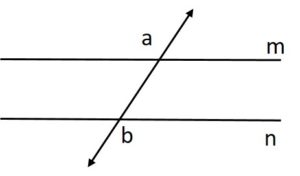
Solution:
Given m || n and ∠a is supplementary to ∠b.
Thus, ∠a = 25o, then ∠b = 180°-25° = 155°.
Hence, ∠b = 155°.
Example 2:
What should be the measurement of the following unknown angle for the given lines to become parallel?
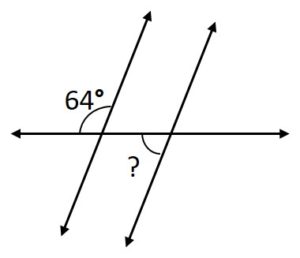
Solution:
Given two parallel lines and to know the measure of an unknown angle.
Thus, one angle is supplementary to another angle. So, name the angle as ∠a and ∠b.
∠a=64° and ∠b=?
∠b=180° – ∠a = 180° – 64° = 116°.
Therefore, the measurement of an unknown angle of two parallel lines is 116°.
Example 3:
Find the parallel line of the given straight line equation 4x – 2y = 6 passing through the coordinate points (1, 2).
Solution:
Given equation is 4x – 2y = 6 and the points are (1, 2)
Slope = -a/b
m = -4/-2 = 2
( x1, y1) = (1, 2)
Parallel line equation is y-y1 = m(x-x1)
y-2 = 2(x-1)
y-2 = 2x-2
y= 2x-2+2
y=2x or 2x-y = 0.
Therefore, the parallel line is 2x-y = 0.
FAQs on Parallel Lines
1. What are parallel lines?
The two lines that do not meet or intersect at any point in a plane and always stay at the same distance if the lengths are extended indefinitely are called parallel lines.
2. What are the types of pairs of angles formed in parallel lines?
The pair of angles formed in parallel lines are corresponding angles, alternate interior angles, alternate exterior angles, and interior angles of the same side of the transversal.
3. What are the real-world examples for parallel lines?
The real-world examples of parallel lines involve railroad tracks, ladders, never-ending rail tracks, opposite edges of a square, rectangle, eraser, and piano keys, etc.
4. How do you find the lines given are parallel?
If we draw the lines infinitely and still they do not intersect at each other then the lines are parallel lines. Furthermore, if the slopes of the two lines are the same then also the given lines are found as parallel lines.
