Triangle is one of the topics in geometry. The word ‘Tri’ in a triangle indicates three. Yes, Triangle is designed with three lines and is shaped as a closed curve with three lines. Each line is considered as a side of the triangle. Totally, one triangle has three sides or faces. The points, where the two sides of the triangle are intersected that particular points are called vertices and the angles are formed at the point of vertices.
Symbol of Triangle
The symbol of the triangle is a closed loop with three sides.
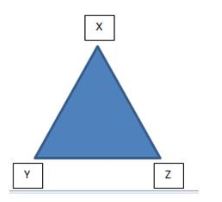
Here, the name of the triangle is XYZ.
Properties of the Triangle
Have a glance at the Properties of Triangle listed below and they are along the lines
- Basically, the triangle has three sides. Here, the sides of the triangle are XY, YZ, and ZX.
- The vertices of the triangle are X, Y, and Z.
- Angles of the triangle are XYZ, YXZ, and XZY.
- The sum of the three angles is equal to 180°.
- The sum of any two sides of the triangle must be greater than the third side of the triangle. That is, XY + YZ = ZX or YZ + ZX = XY or XY + XZ = YZ.
- In Triangles, we have two types of angles. They are interior angles and exterior angles. Interior angles are formed inside of the intersected point of the sides. Exterior angles are formed outside of the intersected points of the sides.
Also, Read:
Area of a Triangle
Area of the Triangle is equal to 1 / 2 * base * height. Here, Area is denoted by ‘A’, the base is denoted by ‘b’ and the height is denoted by ‘h’.
Area (A) = (1 / 2) b*h.
Perimeter of a Triangle
Perimeter of a triangle is equal to half of the sum of the three sides of the triangle. Perimeter is denoted by s and sides of the triangle are denoted as a, b, c.
Perimeter (s) = (a+ b + c) / 2.
- We can find out the area of the triangle by using the perimeter and sides of the triangle. That is, Area = √s(s – a) (s – b) (s – c).
Types of Triangles
We have different types of triangles. Based on the sides and angles, triangles are classified into different types. They are
- Equilateral Triangle
- Isosceles Triangle
- Scalene Triangle
- Acute angled Triangle
- Obtuse angled Triangle
- Right-sided angle Triangle
1. Equilateral Triangle: Three sides of the triangle, as well as three angles of the triangle, are equal and it is called as Equilateral Triangle.
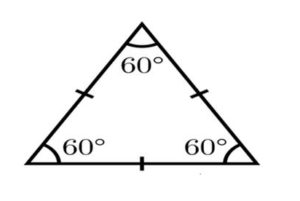
Area of the Equilateral Triangle is equal to √3 / 4 *(side)^2.
2. Isosceles Triangle: In this type of Triangle, two sides of the triangle and two angles are equal.
The area of an Isosceles Triangle is equal to (base * height) / 2.
3. Scalene Triangle: A Triangle that is generated with three different sides and three different angles is called a Scalene Triangle.
Area of the Scalene Triangle is equal to (1 / 2) * base * height.
4. Acute Angled Triangle: Three internal angles of the triangle are measured less than 90° and it is called an Acute Angled Triangle.
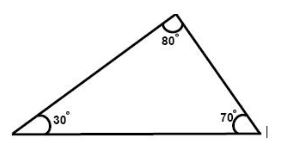
Area of the Acute angled triangle is equal to (1 / 2) * base * height.
5. Obtuse Angled Triangle: Generally, three angles there is a triangle. If any one of the interior angles is measured as greater than 90°, then it is called as Obtuse Angled Triangle.
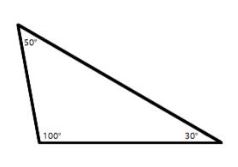
Area of the obtuse angle is equal to (1 / 2) * base * height.
6. Right-sided angle Triangle: The angle between two sides is equal to 90° and the sum of the remaining two angles must be equal to 90°, then it is called a Right-sided angle triangle.
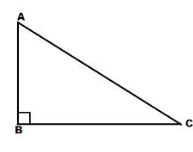
Area of the Right-angled triangle is equal to (1 / 2) * base * height.
Solved Problems on Triangle
1. The Base of the triangle is 4 cm and the height of the triangle is 9 cm. find the area of the triangle?
Solution:
As per the given data, the base of the triangle (b) = 4 cm.
Height of the triangle (h) = 9 cm.
Area of the triangle (A) = (1 / 2) * base * height.
A = (1 / 2) * 4 * 9.
A = 2 * 9 =18 cm².
The area of the triangle is equal to 18 cm².
2. A triangle has an area of 60 cm² and the base of the triangle is 30 cm. Find the height of the triangle?
Solution:
As per the given information, the Area of the triangle (A) = 60 cm².
Base of the triangle (b) = 30 cm².
Area of the triangle (A) = (1 / 2) * base * height.
60 = (1 / 2) * 30 * h.
60 *2 =30 * h.
120 = 30 * h.
H = 120 / 30 = 4 cm.
Height of the triangle = 4 cm.
3. Two sides of the Isosceles triangle are 10 cm each while the third side is 15 cm. Find the area of the isosceles triangle?
Solution:
As per the given data, two sides of the Isosceles triangle = 10 cm
The third side of the triangle = 15 cm.
Area of the Isosceles triangle (A) = √s (s – a) (s – b) (s – c).
S = (a + b + c) / 2
Here, a = 10, b = 10, c =15
S = (10 + 10 + 15) / 2 = 35 / 2 = 17.5
A = √ 17.5 ( 17.5 – 10) (17.5 – 10) ( 17.5 – 15).
A = √17.5 (7.5) (7.5) (2.5) = 588.27.
The area of the Isosceles Triangle is equal to 588.27.
4. Three sides of the triangle are 12 cm, 10 cm, 10 cm. Find the perimeter of the triangle?
Solution:
As per the given information, three sides of the triangle are 12 cm, 10 cm, 10 cm.
Perimeter of the triangle = (a + b + c) / 2.
Here, a = 12 cm, b = 10 cm, c = 10 cm.
Perimeter = (12 + 10 + 10) / 2 = 32 / 2 = 16 cm.
The perimeter of the triangle = 16 cm.
5. Area of the triangle is 20 cm² and the height of the triangle is 60 cm. What is the base of the triangle?
Solution:
As per the given information, the Area of the triangle (A) = 20 cm².
Height of the triangle (h) = 60 cm.
Area of the triangle (A) = (1 / 2) * base * height.
20 = (1 / 2) * base * 60.
20 *2 = base * 60.
40 / 60 = base.
Base = 4 / 6.
The base of the triangle is equal to 2 / 3.
Frequently Asked Questions on Triangle
1. What is Triangle?
Triangle is made up of three lines and it is a closed curve.
2. What are the properties of the Triangle?
Properties of the triangle are
- Triangle has three sides, three angles, and three vertices.
- The Sum of the three angles must be equal to 180°.
- The Sum of any two angles must be greater than the third angle.
3. What are the types of Triangles?
Based on the angles and sides triangles are divided into 6 types. They are
Classification of triangles based on the sides.
- Scalene Triangle
- Isosceles Triangle
- Equilateral Triangle
Classification of triangles based on the angle
- Acute Angle Triangle
- Obtuse Angle Triangle
- Right Angle Triangle
4. What are the basic formulas for triangles?
The basic formulas of triangles are Area and Perimeter Formulas. They are
Area of the Triangle (A) = (1 / 2) * base * height.
Or
Area (A) = √s(s – a) (s – b) (s – c).
Perimeter of the Triangle (s) = (a + b + c) / 2.
5. Difference between the Isosceles triangle and scalene triangle?
Isosceles Triangle: Two sides of the triangle are equal and the third side is different, then it is called as Isosceles Triangle.
Scalene Triangle: If the three sides of the triangle values are different, then it is called a scalene triangle.
