Equal Intercepts theorem helps to find out the various geometrical problems solutions that are used in day-to-day life. In the below sections, we are providing the solved examples along with their explanation. The step-by-step procedure of the equal intercepts theorem helps to understand the problem clearly. Check out all the 9th Grade Math articles on our website.
Read More:
Equal Intercepts Theorem Examples with Solutions
Different Equal Intercepts Theorem Problems are given below with images and explanations. Practice all of them to have enough knowledge of the concept.
Problem 1:
In the below figure, the measurements are given in centimeters. Find out the length of AO if AX = 12.5 cm.
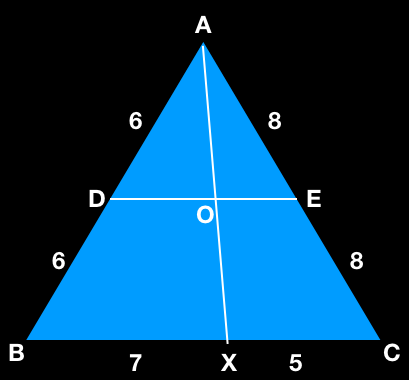
Solution:
As given in the figure,
AD = DB = 6
AE = EC = 8
In the figure, D and E are the midpoints of sides AB and AC respectively.
DE line segment bisects AX at a point O
∴AO = 1/2AX
AO = ½ (12.5)
AO = 6.25
Therefore, the length of AO is 6.25cm
Problem 2. In the given ▵ABC, R is the midpoint of the median AD. If the ▵ABC area is 20 m. Find the area of triangle BRC.
Solution:
Given that, in ▵ABC, R is the midpoint of the median AD
Now, join to B and C
Therefore, it will divide ▵ABC into 2 equal area triangles.
Therefore, area of ▵BRD = Area of ▵BRA
A(▵BRD) = ½ A(▵ARD)
Also, A((▵RDC) = A(▵ARC)
= A((▵RDC) = ½ A(▵ARC)
A(▵BRD) + A((▵RDC) = ½ A((▵ABD) + ½ A((▵ADC)
A(▵BRC) = ½ A(▵ABC) = ½ * 20 = 10m
Therefore, the area of ▵BRC is 10m.
Problem 3.
In the ▵ABC, DE ∥∥ BC, then find the value of EC?
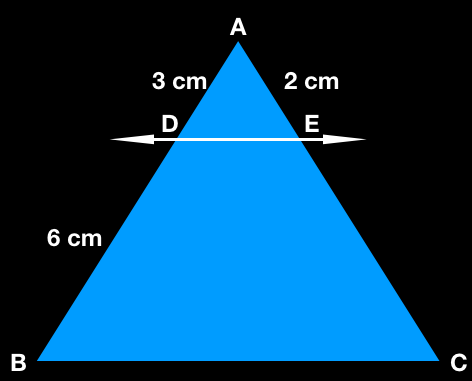
Solution:
Given that DE ∥∥ BC
Based on the basic proportionality theorem, if one line is drawn parallel to one side, then it divides the other sides in an equal ratio.
Hence,
AD/DB = AE/EC
3/6 = 2/EC
½ = 2/EC
EC = 4
Hence, the value of EC is 4.
Problem 4.
What is the size of the ladder he needs if a man wants to get on a flat roof? At 3 meters, there is a bracket sticking on the wall. That bracket shows a shadow 6 meters away from the base. The roof casts a shadow 10 meters from the base. Find the height of the roof?
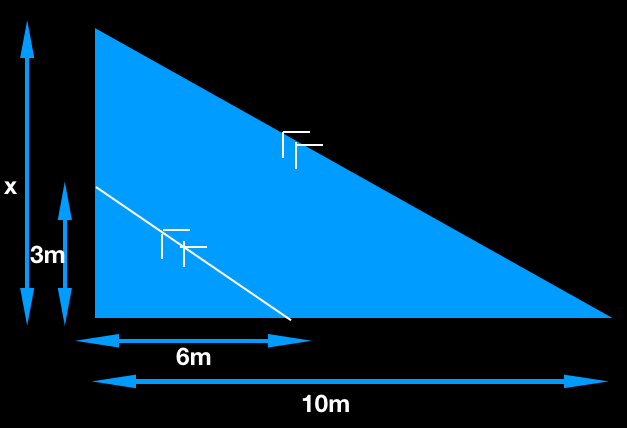
Solution:
Given that, the bracket is sticking at the wall at 3 meters
Based on the basic proportionality theorem, if one line is drawn parallel to one side, then it divides the other sides in an equal ratio.
Therefore,
6/10 = 3/x
By solving the equation,
x = 10 * 3 / 6
x = 5
Therefore, the height of the roof is 5metres.
Problem 5.
Find the value of x in the above diagram?
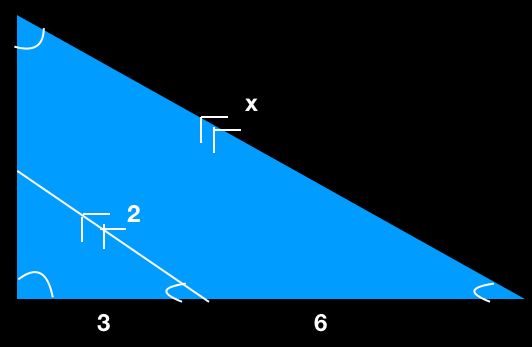
Solution:
As the values of sides are given, based on the basic proportionality theorem, if one line is drawn parallel to one side, then it divides the other sides in an equal ratio.
Therefore, 3/(3+6) is proportional to 2/x
3/9 = 2/x
By substituting the equation further, we get
x = 2 * 9 / 3
x = 18/3
x = 6
Therefore, the value of x is 6.
Problem 6. 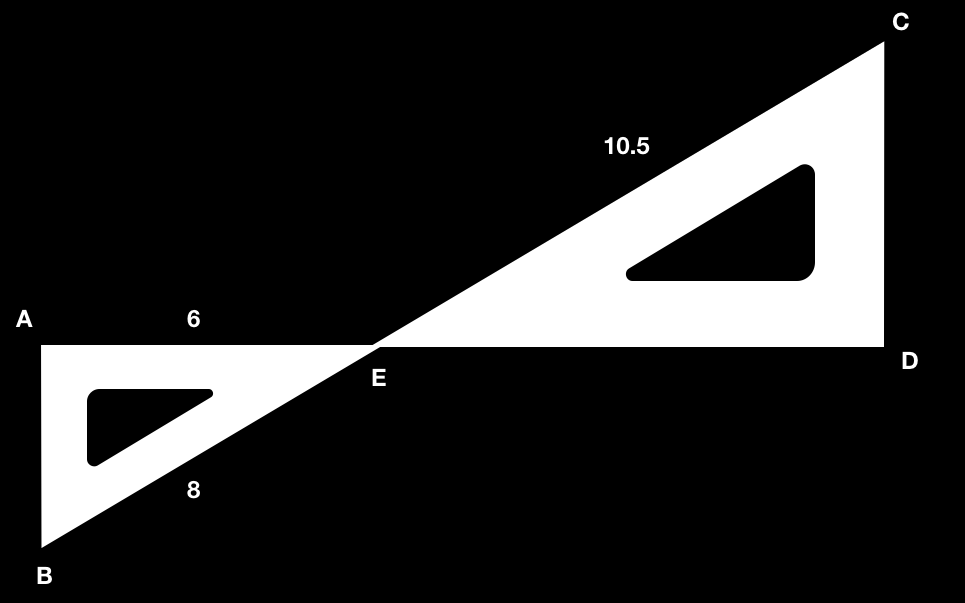
Find the length of ED when AB is parallel to DC in the above diagram?
Solution:
Given that, AB ∥∥ DC
Based on the basic proportionality theorem, if one line is drawn parallel to one side, then it divides the other sides in an equal ratio.
10.5 / 8 = ED / 8
By solving the equation further,
ED = 8 * 10.5 / 8
ED = 10.5
Therefore the length of ED = 10.5
Problem 7. 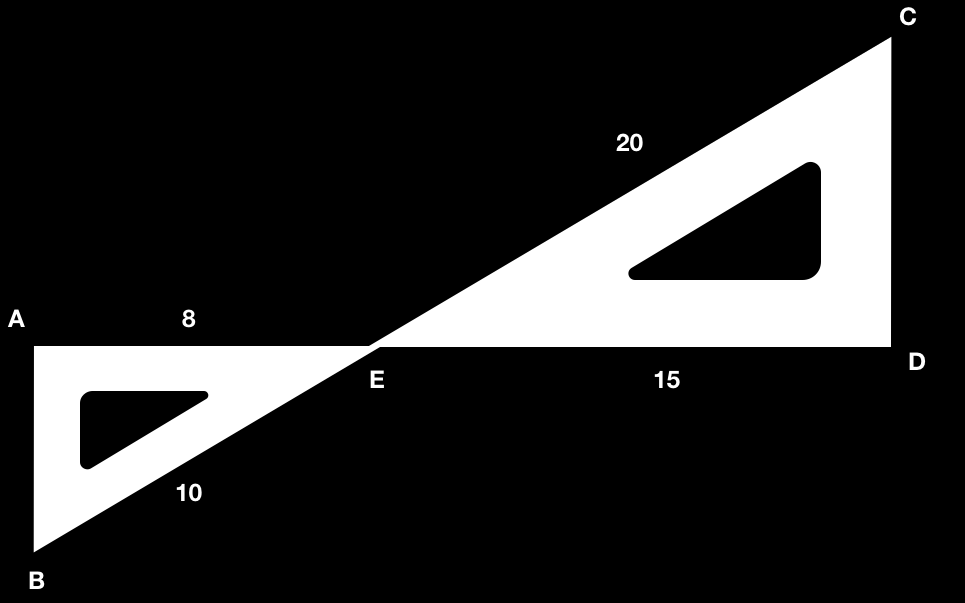
Find if AB and CD are parallel lines?
Solution:
Suppose that both the lines AB and CD are parallel, so they are similar and can be rearranged as:
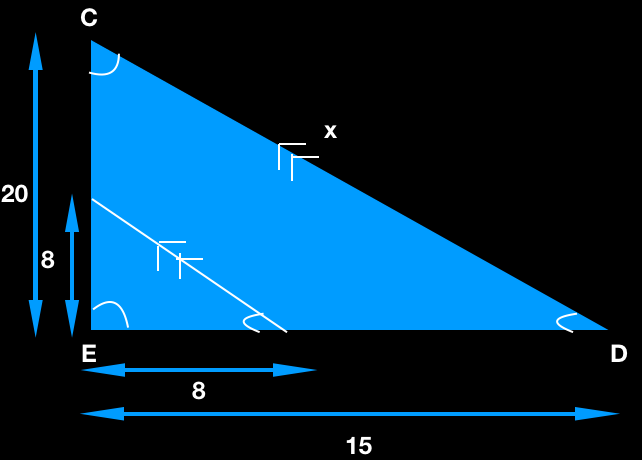
Based on the basic proportionality theorem, if one line is drawn parallel to one side, then it divides the other sides in equal ratio.
8/15 would be proportional to 8/20
8/15 = 0.53
8/20 = 0.4
As the values are different, those lines are not parallel.
Problem 8. Find the length of AB the below diagram?
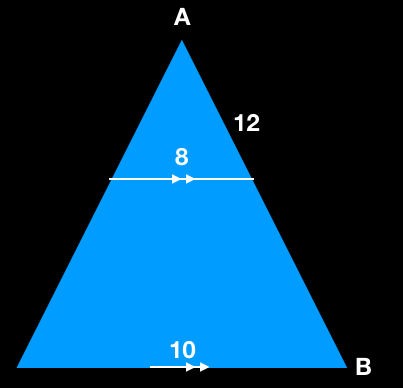
Solution:
Given that, both the sides are parallel,
Based on the basic proportionality theorem, if one line is drawn parallel to one side, then it divides the other sides in an equal ratio.
Therefore,
12/AB = 8/10
AB = 10 * 12 / 8
AB = 120 / 8
AB = 15
The length of AB is 15.
