Get the Construction of Triangles Worksheets from this page. The students can learn how to write the steps of constructions of triangles here. We have provided the different models of questions asked on Triangles Construction in the Worksheet on Construction of Triangles. Here we have given different types of questions on constructing triangles.
5th grade students can get free access to practice the questions on constructing triangles here. Therefore make use of this page and score well in the exams. Worksheet on Constructing Triangles helps students who are lagging in geometry with clear explanations provided.
Do Check:
- Worksheet on Triangle
- To Construct a Triangle whose Three Sides are given
- To Construct a Triangle when Two of its Sides and the included Angles are given
Construction of Triangles Worksheets with Answers
In the Worksheet of constructing triangles, the students can learn to construct the triangle with three sides, constructing the triangle with two angles, constructing a right-angled triangle, and constructing a triangle with two sides and included angles. Go through the given questions and try to solve the given problems
Example 1.
Construct a triangle AB = 5.8cm, BC = 7 cm, AC = 8 cm.
Solution:
Given,
AB = 5.8cm
BC = 7 cm
AC = 8 cm
Steps of Construction of triangle:
Step 1. Draw a line segment AC = 8 cm.
Step 2. Take A as a center and draw an arc with a radius of 5.8 cm.
Step 3. Now take C as a center and draw another arc with a radius of 7 cm.
Step 4. Join AB and BC.
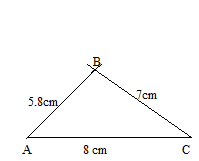
Thus the ABC is the required triangle.
Example 2.
Construct a triangle XYZ in which YZ = 6cm, ZX = 5 cm and XY = 4 cm.
Solution:
Given,
YZ = 6cm
ZX = 5 cm
XY = 4 cm
Steps of Construction of triangle:
Step 1. Draw a line segment YZ = 6 cm.
Step 2. Take Y as a center and draw an arc with a radius of 4 cm.
Step 3. Now take Z as a center and draw another arc with a radius of 5 cm.
Step 4. Join XY and XZ.
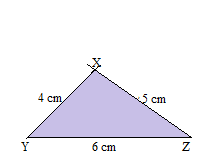
Thus the XYZ is the required triangle.
Example 3.
Construct a triangle ABC in which AB = 6 cm, BC = 6 cm and AC = 6 cm.
Solution:
Given,
AB = 6 cm
BC = 6 cm
AC = 6 cm
Steps of Construction of triangle:
Step 1. Draw a line segment BC = 6 cm.
Step 2. Take B as a center and draw an arc with a radius of 6 cm.
Step 3. Now take C as a center and draw another arc with a radius of 6 cm.
Step 4. Join AB and BC.
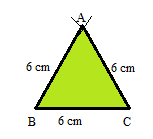
Thus the ABC is the required Equilateral triangle.
Example 4.
Construct a Isosceles triangle PQR whose sides are PQ = 5 cm, QR = 8 cm, PR = 8 cm.
Solution:
Given,
PQ = 8 cm
QR = 5cm
PR = 5 cm
Steps of Construction of triangle:
Step 1. Draw a line segment PQ = 5 cm.
Step 2. Take P as a center and draw an arc with a radius of 8 cm.
Step 3. Now take Q as a center and draw another arc with a radius of 8 cm.
Step 4. Join PR and QR.
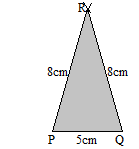
Thus the PQR is the required triangle.
Example 5.
Construct a triangle ABC, in which AB = 7 units, ∠A = 50° and ∠B = 75°.
Solution:
Given,
AB = 7 units
∠A = 50°
∠B = 75°
Steps of Construction of triangle:
Step 1. Draw a line segment AB = 7 units.
Step 2. Take A as a center and a measure of 50° from point A.
Step 3. Now take B as a center and a measure of 75° from point B.
Step 4. Join the point of intersection and label them.
Step 5. The point of intersection is C.
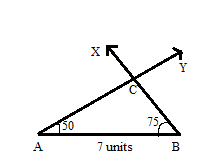
Thus the ABC is the required triangle.
Example 6.
Construct a triangle PQR, in which PQ = 6 cm, ∠P = 60° and ∠Q = 45°.
Solution:
Given,
PQ = 6 cm
∠P = 60°
∠Q = 45°
Steps of Construction of triangle:
Step 1. Draw a line segment PQ = 6 cm.
Step 2. Take P as a center and a measure of 60° from point P.
Step 3. Now take Q as a center and a measure of 45° from point Q.
Step 4. Join the point of intersection and label them.
Step 5. The point of intersection is R.
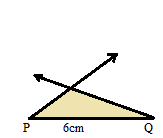
Thus the PQR is the required triangle.
See More Related Articles:
- To Construct a Triangle when Two of its Angles and the included Side are given
- To Construct a Right Triangle when its Hypotenuse and One Side are given
Example 7.
Construct a triangle ABC, in which BC = 7 cm, ∠B = 50° and AB = 4 cm.
Solution:
Given,
BC = 7 cm
∠B = 50°
AB = 4 cm
Steps of Construction of triangle:
Step 1. Draw a line segment BC = 7 cm.
Step 2. Take B as a center and a measure of 70° from point B.
Step 3. Now take B as a center and draw an arc with a radius of 4 cm from B.
Step 4. Join the point of intersection and label them.
Step 5. The point of intersection is A.
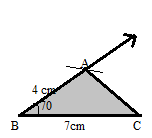
Thus the ABC is the required triangle.
Example 8.
Construct a triangle ABC, in which AB = 5 cm, ∠B = 80° and BC = 3 cm.
Solution:
Given,
AB = 5 cm
∠B = 80°
BC = 3 cm
Steps of Construction of triangle:
Step 1. Draw a line segment AB = 5 cm.
Step 2. Take B as a center and a measure of 80° from point B.
Step 3. Now take B as a center and draw an arc with a radius of 3 cm from B.
Step 4. Join the point of intersection and label them.
Step 5. The point of intersection is C.
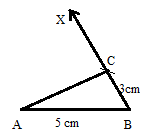
Thus the ABC is the required triangle.
Example 9.
Construct a right triangle ABC in which ∠A = 60°, ∠B = 90° and AB = 6 cm.
Solution:
Given,
∠A = 60°
∠B = 90°
AB = 6 cm
Steps of Construction of triangle:
Step 1. Draw a line segment AB = 6 cm.
Step 2. Take A as a center and a measure of 60° from point A.
Step 3. Now take B as a center and a measure of 90° from point B.
Step 4. Join the point of intersection and label them.
Step 5. The point of intersection is C.
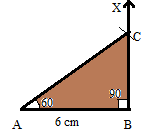
Thus the ABC is the required triangle.
Example 10.
Construct a triangle in which AB = BC = 8 cm and BC = 6 cm.
Solution:
Given,
AB = BC = 8 cm
BC = 6 cm
Steps of Construction of triangle:
Step 1. Draw a line segment BC = 6 cm.
Step 2. Take B as a center and draw an arc with a radius of 8 cm.
Step 3. Now take C as a center and draw another arc with a radius of 8 cm.
Step 4. Join AB and BC.
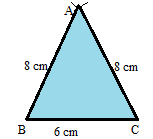
Thus the ABC is the required Isosceles triangle.
