We included HMH Into Math Grade 8 Answer Key PDF Module 3 Lesson 1 Solve Multi-step Linear Equations to make students experts in learning maths.
HMH Into Math Grade 8 Module 3 Lesson 1 Answer Key Solve Multi-step Linear Equations
I Can solve linear equations with integer and rational number coefficients.
Spark Your Learning
Jordan buys 2 new jerseys and a glove for softball. She pays the price shown for the glove and gives the clerk two fifty-dollar bills to pay the exact amount. How much does Jordan pay for each jersey? Write and solve an equation.

Answer:
The equation would be:
2x + 44 = 250
solving the equation:
2x = 250 – 44
2x = 206
x = 206/2
x = 103.
Therefore, jordan pays $103 for each jersey.
What would the equation and solution be if Jordan gives the clerk a single hundred-dollar bill? How are the equations alike or different? How is the process of solving the equations alike or different?

Answer:
If he gives $100 to the clerk then the equation will be:
2x + 44 = 100
2x = 100 – 44
2x = 56
x = 56/2
x = 28.
Turn and Talk Is there another equation that will solve the same problem? Explain.
Build Understanding
1. A batting machine uses an automatic baseball feeder. During baseball practice the feeder is \(\frac{1}{6}\) full. An attendant fills it with 15 baseballs so that the feeder is now \(\frac{2}{3}\) full. How many baseballs does the feeder hold when full?
A. Write an equation to represent the problem.
![]()

Answer:
The equation would be:
1/6 x + 15 = 2/3 x
B. In order to isolate the variable, all terms containing x need to be on one side of the equation. How can you isolate the variable in the equation? What is the resulting equation before simplifying?
_____________________
_____________________
Answer:
1/6 x + 15 = 2/3 x
Simplification:
subtract 15 from both sides
1/6 x + 15 – 15 = 2/3 x – 15
1/6 x = 2/3 x – 15
subtract 2/3 x from both sides
1/6 x – 2/3 x = 2/3 x – 15 – 2/3 x
take out common terms:
x(1/6 – 2/3) = -15
x(1-4/6) = -15
x(-3/6) = -15
X(-1/2) = -15
-1/2 x = -15
C. Solve the equation for x.
Answer:
by continuing the answer from (B)
Multiply both sides by -2
(-1/2 x) (-2) = (-15)(-2)
x = 30
D. Look back at the original equation. How could you use the least common denominator of the fractions to rewrite the equation with integer coefficients? A coefficient is a number multiplied by the
variable.
________________________
Answer:
The original equation:
1/6 x + 15 = 2/3 x
15 = 2/3 x – 1/6 x
15 = x(2/3 – 1/6)
The LCM is 6
15 = x(4 – 1/6)
15 = x(5/6)
15 = 5/6 x
E. What is the new equation? Solve this new equation. Do you get the same solution?
________________________
Answer:
continuing from part (D)
The new equation is 15 = 5/6 x
switching the sides
multiply both sides by 6
(6) (5/6 x) = 15 . 6
5x = 90
x = 18
No we didn’t get the same solution.
This is an example of a linear equation with only one solution.
Turn and Talk Which equation did you prefer to work with? Why?
Step It Out
2. Lanie and Jen buy the same number of books at the used book sale. Lanie buys paperback books and Jen buys hardcover books. Lanie spends $1.50 less than Jen. Solve the equation to find the number of books each of them buys.

1.2n – 1.5 = 0.45n
1.2n = 0.45n + ___
1.2n – ___ = ____
___ = ___
n = ____
Answer:
The given equation:
1.2n – 1.5 = 0.45n
simplification:
1.2n = 0.45n + 1.5
1.2n – 0.45n = 1.5
0.8n = 1.5
n = 1.5/0.8 = 1.89
approximately 2.
Therefore, they buy 2 books each
A. Look at the decimals in the equation and think about how you could rewrite the equation with integer coefficients. What is the least power of 10 you could multiply each term by to eliminate all the decimals?
___________________
Answer:
simplification:
Multiply both sides by 100
1.2n *100 – 1.5 * 100 = 0.45n *100
120n – 150 = 45n
B. Multiply each term of the original equation to eliminate all the decimals. Solve the equation.
1.2n – 1.5 = 0.45n
___ (1.2n) — ___ (1.5) = ___ (0.45n)
___ n – ___ = ___n
___n = ____
n = ____
Answer:
simplification:
Multiply both sides by 100
1.2n *100 – 1.5 * 100 = 0.45n *100
120n – 150 = 45n
add 150 to both sides
120n – 150 + 150 = 45n + 150
120n = 45n + 150
120n – 45n = 150
75n = 150
n = 150/75
n = 2
C. Do you get the same solution?
___________________
Answer:
Yes, both are equal.
D. Which equation was easier to solve? Why?
___________________
Answer:
The equation that is not having decimals because without decimals we can easily simplify the equation.
Turn and Talk How is solving an equation that involves fractions similar to solving an equation with decimals? What methods can you use to solve each
Answer:
Simplify both sides of the equation by combining like terms. If there are fractions, multiply both sides of the equation by the LCD (Least common denominator) of all the fractions. If there are decimals, multiply both sides of the equation by the lowest power of 10 to convert them into whole numbers.
3. Jackie has a coupon for $8 off the price of a jacket. Then the clerk takes 25% off the discounted price, so she saves an additional $10. Determine the original price of the jacket.
A. Write an equation using the Distributive Property, which states that for all real numbers a, b, and c, a(b + c) = ab + ac, and a(b – c) = ab – ac. Convert the percentage to a fraction. Solve the equation.

\(\frac{1}{4}\)(p – 8) = 10
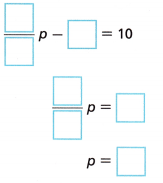
Answer:
The above-given equation:
1/4(p – 8) = 10
use distributive law
1/4 p – 1/4 * 8 = 10
1/4p- 2 = 10
1/4 p = 10 + 2
1/4 p = 12
multiply both sides by 4
4 * 1/4 p = 12 * 4
p = 48
B. Write the original equation, eliminate the fractions, and solve.
\(\frac{1}{4}\)(p – 8) = 10
4[\(\frac{1}{4}\)(p – 8)] = 4(10)
p – ___ = ___
P = ___
Answer:
The above-given equation:
1/4(p – 8) = 10
to eliminate the factors, we need to multiply by 4 both sides
(4) (1/4)[p- 8] = 10 * 4
p – 8 = 40
p = 40+ 8
p = 48
4. Solve the equation 4(2.5x + 2) – x = 26.9.
A. Use the Distributive Property to write an equivalent equation.
__________________
Distributive law:
a(b + c) = ab + ac
Answer:
The given equation:
4(2.5x + 2) – x = 26.9.
(4 * 2.5x + 4 * 2) – x = 26.9
10x + 8 – x = 26.9
B. Combine like terms, terms that have the same variable raised to the same exponent, and solve.
__________________
Answer:
continuing the part (A)
combine like terms:
9x + 8 =26.9
9x = 26.9 – 8
9x = 18.9
x = 18.9/9
x = 2.1
Check Understanding
Question 1.
Anna spent $2.75 at the school store. She bought two erasers and some pencils. How many pencils did she buy? Write and solve an equation.

Answer:
The cost of two erasers = $0.25 x 2 = $0.5
The cost of pencils = P
The amount she spends in school store = $2.75
The equation:
0.5 + 0.75p = 2.75
0.75p = 2.75 – 0.5
p = 2.25/0.75
p = 3
Therefore, she buys 3 pencils.
Question 2.
Solve the equation. Check your solution. \(\frac{1}{5}\)(n – 10) = 6 – 3\(\frac{1}{2}\)
Answer:
The given equation:
1/5(n – 10) = 6 – 3 1/2
convert mixed numbers to improper fractions
3 1/2 = 7/2
1/5(n – 10) = 6 – 7/2
1/5n – 1/5 * 10 = 12 – 7/2
1/5 n – 2 = 5/2
1/5 n = 5/2 + 2
1/5 n = 9/2
multiply both sides by n
5 * 1/5 n = 5 * 9/2
n = 45/2
n = 22.5
On Your Own
Question 3.
The sum of the measures of the angles in the triangle is 180°. What is the measure of each angle? Write and solve an equation.
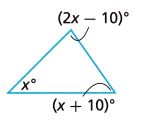
Answer:
(2x – 10) + (x + 10) = 180
(a) = a
2x – 10 + x + 10 + x = 180
4x = 180
x = 180/4
x = 45
Question 4.
Reason Jamie solved the equation \(\frac{2}{3}\)x + 4 = 2 + \(\frac{1}{2}\)x. Is his solution correct? Explain.
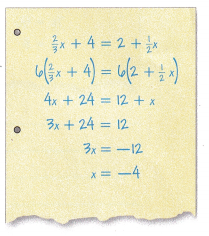
Answer:
The above-given solution:
2/3 x + 4 = 2 + 1/2 x
Simplification:
subtract ‘4’ from both sides
2/3 x + 4 – 4 = 2 + 1/2 x – 4
2/3 x = 1/2 x – 2
subtract 1/2 x from both sides
2/3 x – 1/2 x = 1/2 x – 2 + 1/2 x
1/6 x = -2
multiply both sides by 6
6 . 1/6 x = -2 . 6
x = -12
hence, Jamie is wrong.
Question 5.
Karinne hit 4 more home runs than half the number of home runs Lu hit. Together they hit 10 home runs. Let x represent the number of home runs Lu hit.
A. Write an equation to represent the situation.
______________
Answer:
The equation is:
4 + 1/2x = 10
B. Solve for x.
______________
Answer:
1/2x = 10 – 4
1/2x = 6
x = 12

C. How many home runs did Lu hit?
______________
Answer:
4 + 1/2x= 10 (original equation)
Lu hits 12 home runs.
D. How many home runs did Karinne hit?
______________
Answer:
E. How can you check your answer?
______________
______________
______________
______________
Question 6.
Construct Arguments Max and Corey solve the same equation but they use different methods. Which method would you use? Explain your answer.
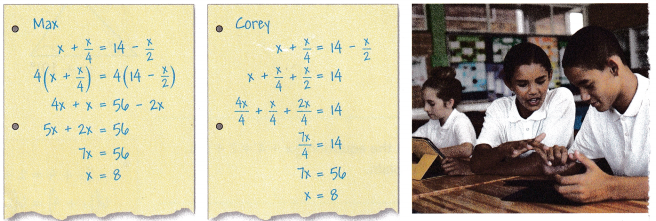
Answer:
I would choose Corey’s answer.
Taking all like terms into one side is easy to calculate.
What Corey did was he grouped all like terms into one side and added all terms.
and then he used the LCM method to complete the simplification.
Question 7.
What is a first step to solve the equation 0.3n – 15 = 0.2n – 5?
______________
Answer:
The above-given equation:
0.3n – 15 = 0.2n – 5
Multiply both sides by 10.
0.3n * 10 – 15 * 10 = 0.2n * 10 – 5 * 10
3n – 150 = 2n – 50
3n – 2n = -50 + 150
n = 100
Solve each equation. Check your solution.
Question 8.
3(x – 2) + 6 = 5(x + 4)
______________
Answer:
The above-given equation:
3(x – 2) + 6 = 5(x + 4)
Simplification:
apply the distributive property.
3x – 6 + 6 = 5x + 20
3x = 5x + 20
subtract 5x from both sides
3x – 5x = 5x + 20 – 5x
-2x = 20
x = -10
Question 9.
2.2(4p + 2) = 13.2
______________
Answer:
The above-given equation:
2.2(4p + 2) = 13.2
simplification:
multiply both sides by 10
2.2(4p + 2) * 10 = 13.2 * 10
22(4p + 2) = 132
divide both sides by 22
22(4p + 2)/22 = 132/22
4p + 2 = 6
4p = 6 – 2
4p = 4
p = 1
Question 11.
2(11t + 1.5t) = 12 – 5t
______________
Answer:
The above-given equation:
2(11t + 1.5t) = 12 – 5t
Simplification:
add similar elements
2(12.5t) = 12 – 5t
25t = 12 – 5t
add 5t to the both sides
25t + 5t = 12 – 5t + 5t
30t = 12
t = 12/30
t =2/5
t = 0.4
Question 12.
\(\frac{7}{8}\)m – \(\frac{1}{2}\) = \(\frac{3}{16}\)m + 5
Answer:
The above-given equation:
7/8 m – 1/2 = 3/16m + 5
simplification:
get all like terms into one side
7/8 m – 3/16 m = 5 + 1/2
7/8 m – 3/16 m = 10 + 1/2
7/8 m – 3/16 m = 11/2
11/16 m = 11/2
multiply both sides by 16
16 * 11/16 m = 11/2 * 16
11m = 88
m= 88/11
m = 8
Question 13.
9(n + 1) = 2(n – 1)
Answer:
The above-givene equation:
9(n + 1) = 2(n – 1)
simplification:
apply the distributive property
9n + 9 = 2n – 2
subtract 2n from both sides
9n + 9- 2n = 2n – 2 – 2n
7n + 9 = -2
7n = -2 – 9
7n = -11
n = -11/7
Question 14.
\(\frac{4}{5}\)x – 3 = \(\frac{3}{10}\)x + 7
Answer:
The above-given equation:
4/5 x – 3 = 3/10 x + 7
add 3 to the both sides
4/5 x – 3 + 3 = 3/10 x + 7 + 3
4/5 x = 3/10 x + 10
subtract 3/10 x from both sides
4/5 x – 3/10 x = 3/10 x + 10 – 3/10 x
x(4/5 – 3/10) = 10
x(8 – 3/10) = 10
x(5/10) = 10
x(1/2) = 10
1/2 x = 10
x = 20
Question 15.
-4(-5 – b) = \(\frac{1}{3}\)(b + 16)
Answer:
The above-given equation:
-4(-5 – b) = 1/3(b + 16)
apply distributive property
20 + 4b = 1/3b + 16/3
subtract 20 from both sides
20 + 4b – 20 = 1/3b + 16/3 – 20
4b = 1/3b + (16 – 60/3)
4b = 1/3b – 44/3
subtract 1/3b from both sides
4b – 1/3b = 1/3b – 44/3 – 1/3b
b(4 – 1/3) = -44/3
b(12 – 1/3) = -44/3
b(11/3) = -44/3
11/3b = -44/3
b = -44/11
b = -4
Question 16.
3.6w = 2(0.8w + 12)
Answer:
The above-given equation:
3.6w = 2(0.8w + 12)
apply distributive property
3.6w = 2 * 0.8w + 12 * 2
3.6w = 1.6w + 24
3.6w – 1.6w = 24
2w = 24
w = 12
I’m in a Learning Mindset!
How is the first step in solving a multi-step linear equation different from the first step in solving a multi-step word problem?
Answer:
The main goal in solving multi-step equations, just like in one-step and two-step equations, is to isolate the unknown variable on one side of the equation while keeping the constant or number on the opposite side.
– Get rid of any grouping symbols such as square brackets, parentheses, etc, by applying the Distributive Property of Multiplication over Addition.
– Simplify both sides of the equation, if possible, by combining like terms.
– Decide where you want to keep the variable because that will help you decide where to place the constant.
– Eliminate numbers or variables by applying opposite operations: addition and subtraction are opposite operations as in the case of multiplication and division.
Lesson 3.1 More Practice/Homework
Solve Multi-step Linear Equations
Question 1.
Elsie is planting a rectangular section of grass.

If the perimeter of the rectangle is 96 feet, what are the length and width of the rectangular section?
Answer:
The perimeter of the rectangle = 2(a + b)
we know that,
the perimeter of the rectangle = 96
length = 6x – 15
width = x
96 = 2(6x – 15 + x)
96 = 2(5x – 15)
now simplify the equation
96 = 10x – 30
96 +30 = 10x
126 = 10x
switching sides
10x = 126
x = 126/10
x = 63/5
x = 12.6
Question 2.
Math on the Spot Solve each equation.
A. 3n + 1 = 19
__________
Answer:
The above-given equation:
3n + 1 = 19
3n = 19 – 1
3n = 18
n = 18/3
n = 6
B. 21 = -2p – 5
__________
Answer:
The above-given equation:
21 = -2p – 5
21 + 2p = -5
2p = -5 – 21
2p = -26
p = -26/2
p = -13
Question 3.
Reason What step would you perform first to solve the following equation? Explain your reasoning.
\(\frac{1}{4}\)(12 – 8x) = \(\frac{2}{3}\)(6x)
Answer:
The above-given equation:
1/4(12 – 8x) = 2/3 (6x)
Multiply fractions: a(b/c) = a . b/c
1* (12 – 8x)/4 = 2/3 (6x)
12 – 8x/4 = 4x
3 – 2x = 4x
3 = 4x + 2x
3 = 6x
switching the sides
6x = 3
x = 1/2
x = 0.5
Question 4.
Heather has a family phone plan. The monthly payment for the family plan includes a $70 charge for unlimited talk and text, a $20 line fee per phone, and a $22.91 equipment fee for each phone. Their total monthly bill is $241.64. Write and solve an equation to find how many phones are on the plan.
Answer:
The number of phones = f
The equation would be:
f($70 + $20 + $22.91) = $241.64
f(112.91) = 241.64
f = 241.64/112.91
f = 2.14
approximately 2 phones.
Therefore, there are 2 phones are on the plan.
Solve each equation. Check your solution.
Question 5.
a + 3(a – 1) = 3(2 + 1)
Answer:
The above-given equation:
a + 3(a – 1) = 3(2 + 1)
simplification:
a + 3a – 3 = 3(3)
a + 3a – 3 = 9
a + 3a = 9 + 3
4a = 12
a = 12/4
a = 3
Question 6.
5y – 3(2 – y) = 10
Answer:
The above-given equation:
5y – 3(2 – y) = 10
simplification:
5y – 6 + 3y = 10
8y – 6 = 10
8y = 10 + 6
8y = 16
y = 16/8
y = 2
Question 7.
1.2x – 2 = 7 + 0.9x
Answer:
The above-given equation:
1.2x – 2 = 7 + 0.9x
multiply both sides by 10
1.2x * 10 – 2 * 10 = 7 * 10 + 0.9x * 10
12x – 20 = 70 + 9x
get all like terms into one side
12x – 9x = 70 + 20
3x = 90
x = 90/3
x = 30
Question 8.
-k + 4(k + 1) = 2k
Answer:
The above-given equation:
-k + 4(k + 1) = 2k
simplification:
-k + 4k + 4 = 2k
3k + 4 = 2k
get like terms on one side
3k – 2k = 4
k = 4
Question 9.
4(\(\frac{x}{6}\) + 5) = 2x + 10
Answer:
The above-givne equation:
4(x/6) + 5 = 2x + 10
4x/6 + 5 = 2x + 10
get like on one side
2/3x – 2x = 10 -5
2x – 6x/3 = 5
-4x/3 = 5
-4x = 15
x = -15/4
Question 10.
3w + \(\frac{w}{2}\) + 1 = 10 – w
Answer:
The above-given equation:
3w + w/2 + 1 = 10 – w
subtract 1 from both sides
3w + w/2 + 1 – 1 = 10 – w – 1
3w + w/2 = 9 – w
multiply both sides by 2
3w * 2 + w/2 * 2 = 18 – w2
6w + w = 18 – w2
7w = 18 – w2
add w2 to both sides
7w + w2 = 18 – w2 + w2
9w = 18
w = 2
Test Prep
Question 11.
Which could be the first step in solving the equation 0.05x + 3 — 0.02x = 4?
A. Add 3 to each side of the equation.
B. Divide each side of the equation by 100.
C. Multiply each side of the equation by 100.
D. Subtract 0.02x from each side of the equation.
Answer: Option C is correct.
The above-given equation;
0.05x + 3 – 0.02x = 4
0.03x + 3 = 4
Multiply both sides by 100
3x + 300 = 400
3x = 100
x = 33.333
Question 12.
Solve the equation. Check your solution.
\(\frac{3}{2}\)(x + 6) = 16 + \(\frac{1}{2}\)(x – 24)
x = ___
Answer:
The above-given equation:
3/2(x + 6) = 16 +1/2(x – 24)
apply distributive property
3/2 x + 3/2 * 6 = 16 + 1/2 x – 1/2 * 24
3/2 x = 1/2 x – 20
subtract 1/2 x from both sides
3/2 x – 1/2 x = 1/2 x – 20 – 1/2 x
x = -20
Question 13.
Laurie earns $7.50 per hour at the fruit stand plus an extra $2.00 per hour on Sundays. One week in August, she worked on Sunday, Monday, and Wednesday. She worked the same number of hours on Monday and on Wednesday. On Sunday she worked 4 hours. If she earned a total of $83.00 for the week, how many hours did Laurie work on Monday? Write and solve an equation.
Answer:
The equation would be:
we don’t know the number of hours so assume it as ‘h’
on Sundays, he works 4 hours and he gets $2 extra.
In a week, he works for three days
7.50 + 2 = 9.50
In the question asked only for Monday hours
2(7.50h) + 9.50(4) = 83
14.50h + 38 = 83
14.50h = 83 – 38
14.50h = 45
h = 45/14.50
h = 3.1 (approximately 3 hours)
Question 14.
Which equation has the solution x = 8?
A. x + 2x – 4 = \(\frac{1}{4}\)(3x + 4)
B. x + \(\frac{1}{2}\)(x + 8) = 4(1 + 3)
C. 2(x – 4) = \(\frac{1}{4}\)(1 + 3) + x
D. x + 4(1 + 3) = \(\frac{1}{2}\)(2x + 4)
Answer: Option B is correct
solve all the equations
x + 1/2(x + 8) = 4(1 +3)
x + 1/2 x + 1/2 . 8 = 16
x + 1/2 x + 4 = 16
x + 1/2 x = 16 – 4
x(1 + 1/2) = 12
x(3/2) = 12
3x/2 = 12
3x = 24
x = 8
Question 15.
Each year Rolando saves 8% of his income. This year he saved $3000; his salary was $2000 less than the previous year. What was his salary in the previous year? Write and solve an equation.
Answer:
The previous income = N
The income he saves each year = 8% of N
In the present year, he saved = $3000
The salary = N – 2000
The equation would be:
8% (N – 2000) = 3000
8/100(N – 2000) = 3000
N- 2000 = 3000 x 100/8
N – 2000 = 37500
N = 37500 + 2000
N = 39500.
Therefore, the previous salary is 39500.
Spiral Review
Question 16.
Triangle ABC is dilated by a scale factor of 1.5 to form Triangle DEF. Are Triangles ABC and DEF congruent? Why or why not?
Answer:
Congruent means when they are the same shape and same size. If triangle ABC is dilated to form triangle DEF, that means that they will have the same shape and the same size. So yes Triangles ABC and DEF will be congruent to one another because they will be the same shape, and they will have the same size as well.
Question 17.
A triangle has angles measuring 45°, 55°, and 80°. It is dilated by a scale factor of 2. What are the angle measures of the dilated image?
Answer:
Dilations preserve angle measures, regardless of the scale factor. Therefore, the angle measures of the image will be the same as that of the pre-image, so our answer is still 4545 °, 5555 °, and 8080 °.
Read More:
