A polygon is a closed 2-D shaped geometric figure that consists of a finite number of sides. All the sides of the polygon are connected with the line segments. The line segments present on the polygon are called edges or sides. The end where two line segments are connected is called corned or vertex. At every corner, an angle is formed. The plane figure-like circle is not treated as a polygon as it doesn’t consist of any sides or angles. In other words, a polygon is a closed figure with three or more sides.
Also, check:
- Different Types of Polygons
- Area of a Polygon
- Convex and Concave Polygons
- Regular and Irregular Polygon
Properties of a Polygon
Depending on the sides and angles, the polygon properties are given below.
- The sum of all the n-sided polygon interior angles is (n – 2) × 180°.
- The measure of an exterior angle of an n-sided regular polygon = 360°/n
- The measure of an interior angle of n-sided regular polygon = [(n – 2) × 180°]/n
- If we take n sides of a polygon, then the number of diagonals = n(n – 3)/2
- The number of triangles formed by joining the diagonals from one edge of a polygon = n – 2
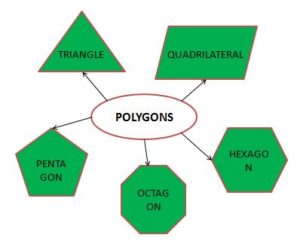
Types of Polygon
There are different types of polygons available based on sides and vertices. The polygons are classified as
- Regular Polygons
- Irregular Polygons
- Concave Polygons
- Convex Polygons
- Trigons
- Quadrilateral Polygons
- Pentagon Polygons
- Hexagon Polygons
- Equilateral Polygons
- Equiangular Polygons
Regular Polygons
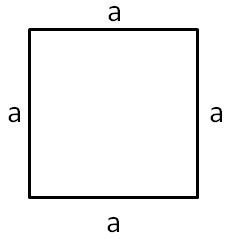
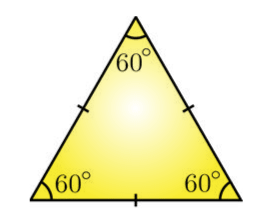
The polygons are called Regular Polygons when all the sides of a polygon are equal and consist of equal interior angles. Equilateral triangles and squares are examples of Regular Polygons.
Examples:
- A regular pentagon consists of 5 equal sides and their interior angles measure 108 degrees.
- A square has all its sides equal to 4cm, and also all the angles are at 90°.
- An equilateral triangle that has all three sides equal to 8cm and angles measure to 60°.
Irregular Polygon
The polygons are called Irregular Polygons when they are in irregular shapes. Also, all the sides of a polygon are not equal and don’t consist of equal interior angles.
Examples:
- A quadrilateral with unequal sides and angles.
- An isosceles triangle consists of only two of its sides equal, and the third side has a different measurement.
Convex Polygon
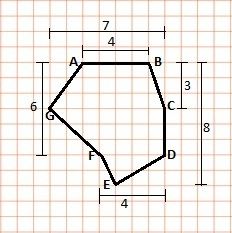
A convex polygon is a polygon when the measure of the interior angle is less than 180 degrees. In a convex polygon, the corners are always present outwards. Convex Polygon is completely opposite to the concave polygon. An irregular hexagon is an example of a convex polygon.
Concave Polygon
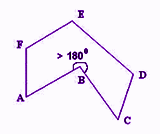
A Concave Polygon is a polygon when one of its angles measures more than 180 degrees. The corners of a concave polygon are present inwards and also outwards.
Trigons
Trigons are defined as three-sided polygons. They are also called triangles. They are Scalene Triangle, Isosceles Triangle, and Equilateral Triangle.
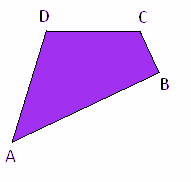
Quadrilateral Polygon
Quadrilateral Polygon is nothing but a polygon that has four sides. A square, rhombus, rectangle, and parallelogram are some of the examples of Quadrilateral Polygons.
Pentagon Polygon
Pentagon Polygon is a polygon consist of five sides. In a regular polygon, all the sides of the Pentagon Polygon are equal. also, in an irregular polygon, all the sides of the Pentagon Polygon are not equal.
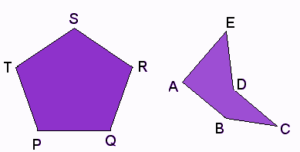
Hexagons
A polygon is defined as a hexagon when it has six sides and six vertices. If all the six sides of a hexagon are equal, then it is known as a regular hexagon. Also, in a regular hexagon, all the interior and also exterior angles are equal.
Want to get more excellence in solving math fundamentals at primary standard? Avail our comprehensive collection of Worksheets, Practice Tests, Word Problems on 4th Grade Math and students can learn great mathematics tricks in no time.
Different Types of Polygon With Sides 3 to 20
We included different polygons along with their sides, vertices, and also angles here. Check out all the polygons to know complete polygons details.
| Polygon Name | Sides | Vertices | Angle |
|---|---|---|---|
| Triangle (also called Trigon) | 3 | 3 | 60° |
| Quadrilateral (also called Tetragon) | 4 | 4 | 90° |
| Pentagon | 5 | 5 | 108° |
| Hexagon | 6 | 6 | 120° |
| Heptagon | 7 | 7 | 128.571° |
| Octagon | 8 | 8 | 135° |
| Nonagon (also called Enneagon) | 9 | 9 | 140° |
| Decagon | 10 | 10 | 144° |
| Hendecagon | 11 | 11 | 147.27 |
| Dodecagon | 12 | 12 | 150 |
| Tridecagon or triskaidecagon | 13 | 13 | 152.3 |
| Tetradecagon or tetrakaidecago | 14 | 14 | 154.28 |
| Pendedecagon | 15 | 15 | 156 |
| Hexdecagon | 16 | 16 | 157.5 |
| Heptdecagon | 17 | 17 | 158.82 |
| Octdecagon | 18 | 18 | 160 |
| Enneadecagon | 19 | 19 | 161.05 |
| Icosagon | 20 | 20 | 162 |
| n-gon | n | n | (n-2)× 180° / n |
Area and Perimeter Formulas of a Polygon
The area of the polygon is defined as the region covered by a polygon and the perimeter of a polygon is the total distance covered by the sides of a polygon. Different polygons formulas of area and perimeter are given below.
| Polygon Name | Area | Perimeter |
|---|---|---|
| Triangle | ½ x (base) x (height) | a + b + c |
| Square | side2 | 4 (side) |
| Rectangle | Length x Breadth | 2(length+breadth) |
| Parallelogram | Base x Height | 2(Sum of pair of adjacent sides) |
| Trapezoid | Area = 1/2 (sum of parallel side)height | Sum of all sides |
| Rhombus | ½ (Product of diagonals) | 4 x side |
| Pentagon | 1/2 x perimeter x apothem | Sum of all five sides |
| Hexagon | 3√3/2 (side)2 | Sum of all six sides |
Angles of a Polygon
A polygon has different sides and every corner of it forms an angle. Mainly, there are two types of angles classified as below.
Interior Angle Property
The sum of all the interior angles of a simple n-gon = (n − 2) × 180°
We can also write it as Sum = (n − 2)π radians Where ‘n’ is equal to the number of sides of a polygon.
Example: A quadrilateral has four sides, therefore, the sum of all the interior angles is given by:
Sum of interior angles of 4-sided polygon = (4 – 2) × 180° = 2 × 180° = 360°
Exterior Angle property
The sum of interior and the corresponding exterior angles at each end of any polygon are supplementary to each other.
- Interior angle + Exterior angle = 180 degrees
- Exterior angle = 180 degrees – Interior angle
Frequently Asked Questions on Polygon
1. What is a polygon?
A polygon is a closed two-dimensional geometrical shape that has a finite number of sides.
2. What are the different types of polygons?
The different types of polygons are
1. Regular polygon
2. Irregular polygon
3. Convex polygon
4. Concave polygon
3. What is called a polygon with 4 sides?
A polygon with 4 sides is called a Quadrilateral.
4. How many diagonals does a polygon have?
If we consider a polygon with n sides, then the polygon will have n(n – 3)/2 diagonals. Triangles do not have diagonals.
