Are you feeling difficulty constructing triangles? If yes, then need not worry about it. Constructions are the easiest and scoring topic in maths. Learn how to Construct a Triangle when Two of its Angles and the included Side are given from here. See the Question and Answers on constructing a triangle when two of its angles and the included Side are given.
Two angles and side is known as ASA (Angle-Side-Angle). See the construction steps from this page. We will help you to construct a triangle with two angles and one side in a simple method. Get the step-by-step explanation for all the questions here.
Do Refer:
- To Construct a Triangle whose Three Sides are given
- To Construct a Triangle when Two of its Sides and the included Angles are given
How to Construct a Triangle when Two Angles and One Side(ASA) is given?
There are four steps to construct a triangle.
Step 1. Draw the line segment.
Step 2. Using a protractor draw a ray making an angle with the line segment.
Step 3. Using a protractor at another point draw another arc.
Step 4. By using the property “Sum of the three angles of any triangle is 180°. With this property, we can find the third angle.
Practice Math Online with Unlimited Questions provided in 5th Grade Math Activity Sheets and become a blossoming mathematician in no time.
Construction of Triangle with Two Angles and One Side Examples
Example 1.
Draw a triangle ABC in which ∠B = 60° and ∠C = 70° and the side BC = 6 cm.
Solution:
Step 1. Draw the line segment BC.
Step 2. Using a protractor draw a ray making a 60° angle with the line segment BC = 6 cm.
Step 3. Using a protractor draw another angle with a measure of 70 degrees at another point draw another arc with C as the center.
Step 4. By using the property “Sum of the three angles of any triangle is 180°. With this property, we can find the third angle.
Step 5. Join PB and QC.
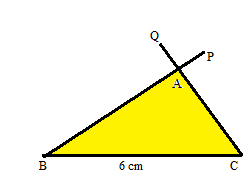
Thus the required triangle ABC is formed.
Example 2.
Draw a triangle ABC in which ∠B = 40° and ∠C = 50° and the side BC = 8 cm.
Solution:
Step 1. Draw the line segment BC = 8cm.
Step 2. Using a protractor draw a ray making a 40° angle with the line segment BC = 8 cm.
Step 3. Using a protractor draw another angle with a measure of 70 degrees at another point draw another arc with C as the center.
Step 4. By using the property “Sum of the three angles of any triangle is 180°. With this property, we can find the third angle.
Step 5. Join PC and QB.
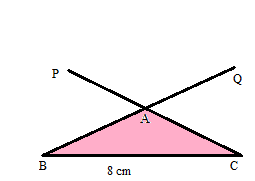
Thus the required triangle ABC is formed.
Enhance your skills by practice more problems on geometry on 5th grade math which includes worksheets, practice tests, examples etc.
Example 3.
Draw a triangle XYZ in which ∠Y = 100° and ∠X = 50° and the side XY = 8 cm.
Solution:
Step 1. Draw the line segment XY = 5cm.
Step 2. Using a protractor draw a ray making a 100 ° angle with the line segment XY = 8 cm.
Step 3. Using a protractor draw another angle with a measure of 50 degrees at another point draw another arc with Y as the center.
Step 4. By using the property “Sum of the three angles of any triangle is 180°. With this property, we can find the third angle.
Step 5. Join PX and QY.
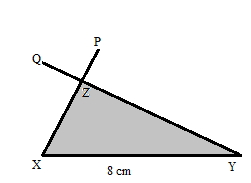
Thus the required triangle XYZ is formed.
Example 4.
Draw a triangle ABC in which ∠CAB = 55° and ∠CBA = 70° and the side AB = 5 cm.
Solution:
Step 1. Draw the line segment AB = 5cm.
Step 2. Using a protractor draw a ray making a 55° angle with the line segment AB = 5 cm.
Step 3. Using a protractor draw another angle with a measure of 70 degrees at another point draw another arc with B as the center.
Step 4. By using the property “Sum of the three angles of any triangle is 180°. With this property, we can find the third angle.
Step 5. Join AQ and PB.
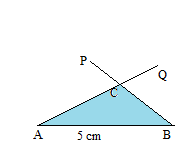
Thus the required triangle ABC is formed.
Example 5.
Draw a triangle PQR in which ∠RPQ = 80° and ∠RQP = 55° and the side PQ = 8 cm
Solution:
Step 1. Draw the line segment PQ = 8cm.
Step 2. Using a protractor draw a ray making a 80° angle with the line segment PQ = 8 cm.
Step 3. Using a protractor draw another angle with a measure of 55 degrees at another point draw another arc with Q as the center.
Step 4. By using the property “Sum of the three angles of any triangle is 180°. With this property, we can find the third angle.
Step 5. Join PR and RQ.
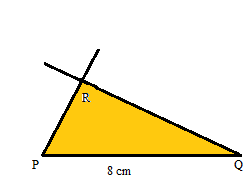
Thus the required triangle PQR is formed.
