Multiplication is one of the basic arithmetic operations that every student must learn in primary school. It is nothing but the repeated addition of two numbers. If you add two numbers more than once, then you can represent a product. We can learn the steps to multiply a one-digit number by 2 digit number or3 digit number or multiply 2 digit number by 2 digits or 3 digit number. We also have different methods to solve the product of them.
Also, Refer:
What is meant by Multiplication?
Multiplication is the result of combing groups of equal sizes. It is one of the arithmetic operations and it is represented by the cross (x) or dot (.) or astrict (*) symbol. Multiplication operation is performed instead of continuously adding the same quantity to the given quantity. So, it is also called as repeated addition.
Examples:
1. 4 x 7 = 28
Add the number 7, 4 times
7 + 7 + 7 + 7 = 28
2. 5 x 6 = 5 + 5 + 5 + 5 + 5 + 5 = 30
Parts of Multiplication & Formula
Every multiplication question has exactly three terms they are multiplier, multiplicand, and product. Discuss each of them in detail in the following sections.
- Multiplier: It is a number by which the multiplicand is multiplied.
- Multiplicand: It is the second number that to be multiplied by the multiplier.
- Product: The result of the multiplication of two numbers is the product.
The formula of multiplication is Product = Multiplier x Multiplicand.
The numbers that are being multiplied (multiplicand, multiplier) are called the factors of the product.
Examples:
8 x 4 = 32
Here in the above example, 8 is the multiplier, 4 is the multiplicand and 32 is the product.
6 x 7 = 42
Here, 6 is the multiplier, 7 is multiplicand, and 42 is the product.
Multiplication Properties
Following are the four important Properties of Multiplication.
1. Associative Property:
It states that the grouping of numbers does not affect the product when multiplying a series of numbers.
Examples:
For the product of two numbers:
2 x 3 = 3 x 2 = 6
For the product of 3 numbers
5 x (6 x 7) = (5 x 6) x 7 = 210
2. Distributive Property
It states that the mathematical expression has addition or subtraction of values multiplied by a number is similar to the sum or difference of numbers followed by multiplication. Expressed as m x (n + p) = m x n + m x p or m x (n – p) = m x n – m x p
Examples:
8 x (15 – 6) = 8 x 15 – 8 x 6
8 x (9 + 6) = 8 x 9 + 8 x 6
3. Commutative Property
It states that the change in the order of multiplication of two or more numbers does not show an impact on the result.
Examples:
5 x 3 = 3 x 5
6 x 4 x 1 = 4 x 1 x 6
4. Identity Property
It states that if any number is multiplied by 1 gives the same number as the answer.
Examples:
8 x 1 = 8
1 x 4 = 4
How to Compute Multiplication of 2 Numbers?
The four simple ways to multiply 2 numbers are given here. They are multiplication using repeated addition, long multiplication, using expanded notation, and using the number line.
Repeated Addition Method:
- Take any two numbers to find their product.
- The multiplier should be added to the multiplicand.
- Again add multiplicand to the sum.
- Repeat the process a multiplicand number of times.
- The final sum is the product of 2 numbers.
Long Multiplication Method:
- Get multiplicand and multiplier
- Enter multiplicand, the multiplier in two different column
- Multiply the unit digit of the top number by the unit digit of the bottom number and write the product below.
- Multiply the unit digit of the bottom number by ten digits of the top number and write the product.
- Likewise, multiply all digits of the top number by the bottom number. If you get the product as a two-digit number, write the unit digit of the result below and the tens digit is the carry.
- Next, multiply all top number digits with the tens digit of the bottom number.
- Likewise, complete the multiplication of all numbers.
- Add the result of units, tens digit numbers to get the final product.
Expanded Notion Method:
- Represent the given multiplicand in the expanded form
- Multiply the multiplier by each digit of the expanded multiplicand.
- Find the sum of the results to obtain the final product.
Number line Method:
- Draw a number line.
- Mark the first number and add the second number to it.
- Repeat the process a multiplicand number of times to find the product.
Also, Read
- Multiplying 2-Digit Number by 1-Digit Number
- Multiplying 1-Digit Number
- Column Method Multiplication
- Expansion Method of Multiplication
Solved Examples on Multiplication
Example 1:
Solve 156 x 92 using the long multiplication method.
Solution:
Given that,
156 x 92
multiplier = 156
multiplicand = 92

Product = 14,352
So, 156 x 92 = 14,352
Example 2:
Solve 143 x 5 using the expanded notation.
Solution:
Given that,
143 x 5
The expanded notion of 143 = 100 x 1 + 10 x 4 + 1 x 3
= 100 + 40 + 3
143 x 5 = (100 + 40 + 3) x 5
= 100 x 5 + 40 x 5 + 3 x 5
= 500 + 200 + 15
= 700 + 15
= 715
So, 143 x 5 = 715
Example 3:
Solve 18 x 9 using the repeated addition.
Solution:
Given that,
18 x 9
multiplier = 18
multiplicand = 9
Add 18, 9 times repeatedly.
18 x 9 = 18 + 18 + 18 + 18 + 18 + 18 + 18 + 18 + 18
= 162
Therefore, 18 x 9 = 162
Example 4:
Compute 8 x 6 using the number line process.
Solution:
Given that,
8 x 6
8 is added 6 times.
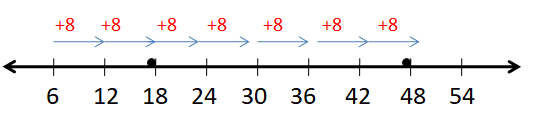
Therefore, 8 x 6 = 48
Example 5:
Solve 256 x 172.
Solution:
Given that,
256 x 172

Therefore, 256 x 172 = 44032.
