Into Math Grade 3 Module 20 Lesson 3 Answer Key Categorize Plane Shapes

We included HMH Into Math Grade 3 Answer Key PDF Module 20 Lesson 3 Categorize Plane Shapes to make students experts in learning maths.

HMH Into Mat

h Grade 3 Module 20 Lesson 3 Answer Key Categorize Plane Shapes

I Can identify whether a plane shape belongs in a category by the number of parallel sides, sides of equal length, and right angles.

Spark Your Learning

Louise and Paul play a game that has cards with shapes on them. Each shape in the game represents a different move on the game board. How can Louise and Paul sort the shapes below?

Show one way to sort the shapes by their attributes.

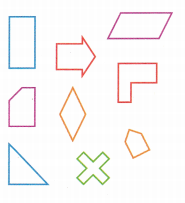
Answer:
First of all, need to know what is an attribute?
An attribute is a characteristic, or feature of an object.
We can sort by their shape, colour, size, and thickness.
Here in the objects, we can sort by the colour:

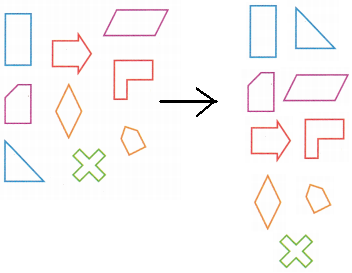
Turn and Talk Describe another way in which Louise and Paul could sort the shapes. Explain how the ways to sort the shapes are the same and different.
Answer:
Another way Louise and Paul could sort the shapes are by observing their shapes, size, and thickness. In the above question, we sorted by colour. Well, they are just a method of arranging shapes so that they make sense to you.
This is another way they can sort by their size:

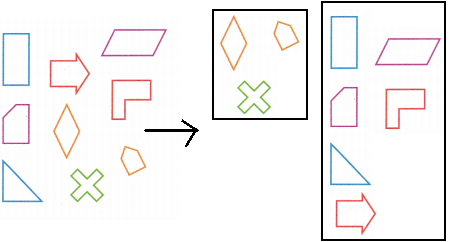
The shapes in the small box represent the small sizes.
The shapes in the large box represent the big sizes.

Build Understanding

Question 1.
Louise and Paul use a Venn diagram to sort shapes.

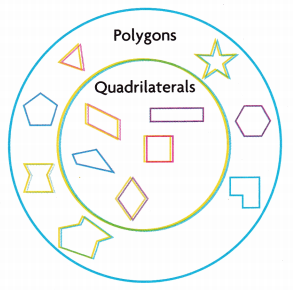
A. How are the polygons within the outer circle of the diagram related to one another?
Answer:
The polygons are similar when the corresponding angles are equal/congruent, and the corresponding sides are in the same proportion. These main things make one polygon similar to another polygon.

B. How are the quadrilaterals within the inner circle related to one another?
Answer:
There are many different types of quadrilaterals and they all share the similarity of having four sides, two diagonals and the sum of their interior angles is 360 degrees. They all have relationships with one another, but they are not exactly alike and have different properties.

C. How are the polygons as a category related to the quadrilaterals as a category?
Answer: They are similar, in that they are two-dimensional figures with three or more sides.
Polygons are usually shaped like triangles, squares.
Poly means many and gon means angles. This can be written as many angled figures.
A polygon is a closed figure made of line segments that do not cross.
For example, if we take a triangle related to quadrilateral: In quadrilateral there are four sides. The quadrilateral will be divided into two triangles. That triangle is half of a quadrilateral, therefore the angle measurements of a triangle are half of the angle measurements of a quadrilateral.

D. Draw a shape into each circle of the diagram. Explain how your shapes belong in that circle.
Answer:
If I draw a square then it belongs to the outer circle and inner circle because the square has four sides, four corners, and they are made with straight lines.

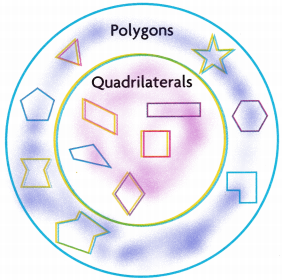
The circle cloured with blue are polygons is a plane figure that is described by a finite number of straight-line segments connected to form a closed polygonal chain.
The circled coloured with pink are quadrilaterals. It is a plane figure that has four sides or edges, and also has four corners or vertices. The angles are present at the four vertices or corners of the quadrilateral.

E. Draw a shape that does not belong in either circle of the diagram. Explain why it does not belong.
Answer:

These are not quadrilaterals because quadrilaterals have four sides, four edges and four corners. A Quadrilateral is a polygon having a number of sides equal to four. That means a polygon is formed by enclosing four line segments such that they meet at each other at corners/vertices to make 4 angles. That’s why the above diagrams do not belong to the quadrilaterals circle.

The above diagrams are not polygons because polygons are closed figures with three or more sides. A minimum of three line segments is required to connect end to end, to make a closed figure. Thus a polygon with a minimum of three sides is known as Triangle and it is also called 3-gon. An n-sided polygon is called n-gon. But in the above diagrams, there are curve shapes so the above diagrams do not belong to polygons circle.

Turn and Talk Is a quadrilateral always a polygon? Is a polygon always a quadrilateral? Explain.
Answer:
Yes, a quadrilateral is always a polygon because a quadrilateral has four sides, four edges and four corners. A Quadrilateral is a polygon having a number of sides equal to four. That means a polygon is formed by enclosing four line segments such that they meet at each other at corners/vertices to make 4 angles.
but polygons are not always quadrilaterals because polygons are closed figures with three or more sides. A minimum of three line segments is required to connect end to end, to make a closed figure. Thus a polygon with a minimum of three sides is known as Triangle and it is also called 3-gon. An n-sided polygon is called n-gon.

Question 2.
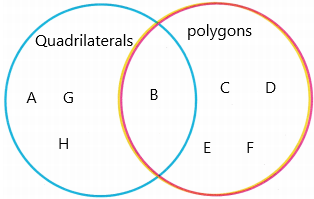
Here is a group of plane shapes.

A. Which of the plane shapes are quadrilaterals? Write the letter of the shape.
Answer: A, B, G, H
Quadrilaterals are polygons. They are part of a plane enclosed by four sides (quad means four and lateral means side). All quadrilaterals have exactly four sides and four angles. They can be sorted into specific groups based on the lengths of their sides or measures of their angles.

B. Which of the plane shapes are polygons with all sides of equal length? Write the letter of the shape.
Answer: C, D, E, F
When all the five sides of the polygon are equal in length, then it is called regular pentagon otherwise irregular pentagon. Hexagons Another type of polygon is the hexagon which has 6 sides and 6 vertices. A regular hexagon will have equal 6 sides and all its interior and exterior angles also measure equals.

C. Use the Venn diagram to sort and compare the shapes. Label each circle of the diagram. Place the letter of each shape in the diagram.

Answer:
A diagram used to represent all possible relations of different sets. A Venn diagram can be represented by any closed figure, whether it be a Circle or a Polygon (square, hexagon, etc.). But usually, we use circles to represent each set.
Polygons with sides of equal length.
A quadrilateral is a plane figure that has four sides or edges, and also has four corners or vertices. The angles are present at the four vertices or corners of the quadrilateral.

Check Understanding

Question 1.
Circle the plane shapes that are polygons with exactly one pair of equal-length sides. Draw a line through the shapes that appear to have exactly one pair of parallel sides.

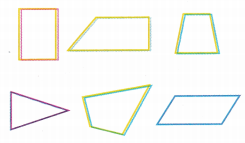
Answer:
Trapezoid: Four straight sides, and has exactly one pair of opposite sides that are parallel.
Only trapezoids have exactly one pair.

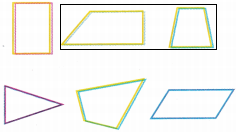
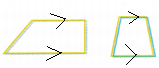
Marking parallel lines on shapes that appear to have exactly one pair of parallel sides.
Definition: parallel lines are coplanar straight lines that do not intersect at any point. They are always parallel and are at equidistant from each other. Parallel lines are non-intersecting lines. We can also say Parallel lines meet at infinity.

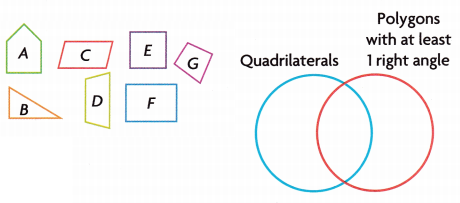
On Your Own

Complete the Venn diagrams.

Question 2.
Place the letter of each shape in the correct place in the Venn diagram.

Answer:

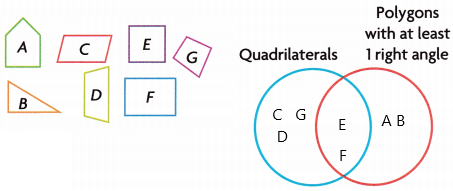
Polygons are simply closed figures formed by line segments in the same plane.
Polygon characteristics:
1. Only straight line segments.
2. No curves.
3. Must have at least 3 line segments.
4. Figure must be a closed shape.
5. Line segments meet only the endpoint.
6. Lines cannot cross in the middle.
Quadrilateral characteristics:
1. Straight line segments
2. 4-sides

Question 3.
Place the letter of each shape in the correct place in the Venn diagram.

Answer:

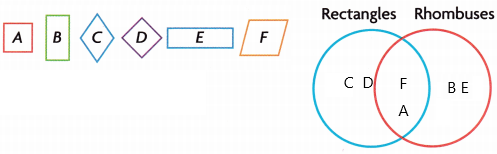
A rectangle is a square when both sides are equal, opposite sides are equal, all angles are equal, opposite angles are equal, and when they bisect each other, the sum of two adjacent angles is 180.
A rectangle can be a rhombus because opposite sides are equal, opposite sides are parallel, opposite angles are equal, bisect each other, the sum of two adjacent angles is 180.
According to the properties, we can say the types of rectangles and rhombuses.

Question 4.
Open-Ended Choose two different quadrilaterals to compare. How are they the same? How are they different?
Answer:
For example, if we choose rectangle and parallelogram by these two quadrilaterals we can say how they are the same and different.
They are not having the same sides.
– According to the properties of rectangle and parallelogram, all sides are not the same.
– Moreover, opposite sides are equal
– Opposite sides are parallel
– Opposite angles are equal
– Sum of adjacent angles is 180
– They are bisected each other.
– One more same thing is that they do not bisect perpendicularly.
Now writing the differences:
– They are different in angles.
– In a rectangle all angles are equal but in a parallelogram, all angles are not equal.

Question 5.
Reason Is a square always a rhombus? Is a rhombus always a square? Explain.
Answer:
Is square a rhombus?
Rhombus has all its sides equal and so does a square. Also, the diagonals of the square are perpendicular to each other and bisect the opposite angles. Therefore, a square is a type of rhombus.
No, a rhombus is not a square but a square can be a rhombus.
Why is a rhombus not a square?
Rhombus is not a square since for a square all the sides are equal and all the interior angles are equal right angles. However, in the rhombus, all the interior angles are not equal even though they have equal sides.
In a $\text{rhombus}$
$\text{All the sides are equal.}$
$\text{The opposite sides are parallel}$
$\text{The opposite angles are equal}$
$\text{The diagonals bisect each other at 90°}$
$\text{The diagonals bisect the angles at the vertices}$
$\text{there are 2 lines of symmetry}$
$\text{it has rotational symmetry of order 2}$
A square has all the properties of a rhombus, with more properties –
In a $\text{square:}$
$\text{All the sides are equal.}$
$\text{The opposite sides are parallel}$
$\text{The opposite angles are equal}$
$\text{All the angles are equal to 90°.}$
$\text{The diagonals bisect each other at 90°}$
$\text{The diagonals are equal.}$
$\text{The diagonals bisect the angles to give 45° angles}$
$\text{there are 4 lines of symmetry}$
$\text{it has rotational symmetry of order 4 A rhombus does NOT have all the properties of a square, therefore is not a special kind of square.}$

I’m in a Learning Mindset

What strategy for categorizing plane shapes have I not yet tried?
Answer: