We included HMH Into Math Grade 3 Answer Key PDF Module 20 Lesson 2 Categorize Quadrilaterals to make students experts in learning maths.
HMH Into Math Grade 3 Module 20 Lesson 2 Answer Key Categorize Quadrilaterals
I Can identify whether a shape belongs in a group by the number of sides, number of angles, sides that are equal in length, parallel sides, and by some shape names and attributes.
Spark Your Learning
Sydney uses computer programing to draw a quadrilateral that has at least one pair of parallel sides.

Draw three or more shapes that the computer might draw.

Answer:
A trapezoid is a polygon that has only one pair of parallel sides. These parallel sides are also called parallel bases of trapezoid. The other two sides of trapezoids are non-parallel and called legs of trapezoids. There is some disagreement over the definition of trapezoids. One school of mathematics considers that a trapezoid can have one and only one pair of parallel sides, while the other argues that there can be more than one pair of parallel sides in a trapezoid. If we consider the second definition, a parallelogram is also a trapezoid according to that. But the first definition does not consider a parallelogram to be a trapezoid. Since we have already mentioned it as one of the types of quadrilateral.
Right trapezoids:
A Right trapezoid is a trapezoid that has a pair of right angles, adjacent to each other. It is used while evaluating the area under the curve, under that trapezoidal rule.
Isosceles trapezoids:
If the non-parallel sides, or we can say, the legs of a trapezoid are equal in length, it is known as an Isosceles trapezoid.
Scalene Trapezoids:
When neither the sides nor the angles of a trapezium are equal, we call it a Scalene trapezoid.
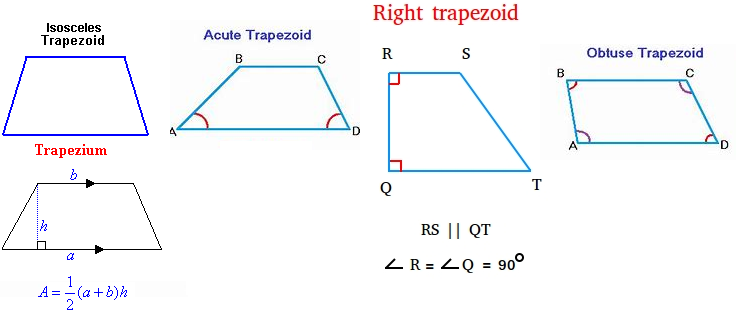
Area of Trapezoid:
The area of a trapezoid can be calculated by taking the average of the two bases and multiplying it with the altitude. The area formula for trapezoids is given by-
Area=1/2(a+b)h.
Turn and Talk Sydney now codes a program to draw a quadrilateral with four sides of equal length and at least one right angle. What quadrilateral will the computer draw? Explain how you know.
Answer: The computer would draw squares.
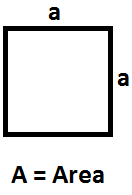
A square is a quadrilateral in which all four sides are equal in length and all the angles are equal. All the angles are equal to 90 degrees i.e. they are right angles. A square is also a parallelogram as the opposite sides are parallel to each other. Also, the diagonals are perpendicular to each other and are also of equal length. A quadrilateral can only be called a square if it satisfies both the properties of rectangle and rhombus.
Properties of square:
– All sides and angles are congruent.
– Opposite sides are parallel to each other.
– The diagonals are congruent.
– The diagonals are perpendicular to and bisect each other.
– A square is a special type of parallelogram whose angles and sides are equal.
– Also, a parallelogram becomes a square when the diagonals are equal and right bisectors of each other.
Build Understanding
Question 1.
Place the quadrilaterals into the correct categories. Some shapes may belong to more than one category.
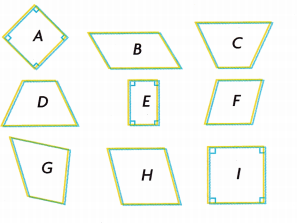
A. Quadrilaterals: __________
How do you know that a shape is a quadrilateral?
Answer: The above-shown shapes are all quadrilaterals. rhombus, square, rectangle, parallelogram, trapezoid.
A quadrilateral is a closed shape and a type of polygon that has four sides, four vertices and four angles. It is formed by joining four non-collinear points. The sum of interior angles of quadrilaterals is always equal to 360 degrees. The types of quadrilaterals are defined based on the measure of the angles and lengths of their sides. As the word ‘Quad’ means four, all these types of a quadrilateral have four sides, and the sum of angles of these shapes is 360 degrees. The list of types of quadrilaterals are: Trapezium; Parallelogram; Squares; Rectangle; Rhombus; Kite
B. Rhombuses: ____________
How do you know that a shape is a rhombus?
Answer: 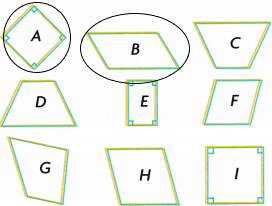
* A rhombus can also be called a type of parallelogram because its sides are parallel to each other. The sum of angles in a rhombus is 360°. Opposite angles are equal to each other and adjacent angles are supplementary angles.
* A rhombus is a type of parallelogram, and what distinguishes its shape is that all four of its sides are congruent. There are several formulas for the rhombus that have to do with its: All 4 sides are congruent. Diagonals bisect vertex angles. Diagonals are perpendicular.
* It is considered a special parallelogram, and because of its unique properties, it gets an individual identity as a quadrilateral. Rhombus is also called an equilateral quadrilateral, since equilateral means that all of its sides are equal in length.
C. Parallelograms: ____________
How do you know that a shape is a parallelogram?
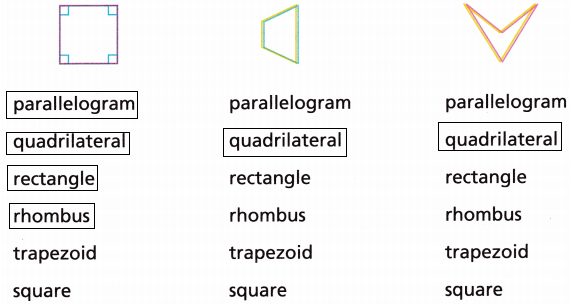
Answer: 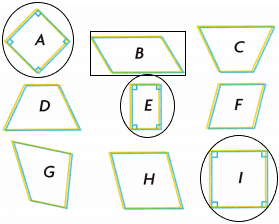
* If a parallelogram has perpendicular diagonals, you know it is a rhombus. So I’m thinking of a parallelogram that is both a rectangle and a rhombus.
* If two consecutive sides of a parallelogram are congruent, then it’s a rhombus (neither the reverse of the definition nor the converse of a property). If either diagonal of a parallelogram bisects two angles, then it’s a rhombus (neither the reverse of the definition nor the converse of a property).
* Why it is a rectangle: Because the measures of the interior angles of a quadrilateral add up to 360, you can show that all four angles of our parallelogram are right angles. That’s more than enough to make your parallelogram a rectangle.
* The only parallelogram that satisfies that description is a square. According to the theorem, If the diagonals of a parallelogram are congruent and perpendicular, the parallelogram is a square.
D. Trapezoids that are defined as having exactly one pair of parallel sides: ____________
How do you know that a shape is a trapezoid?
Answer: Quadrilateral
– Trapezoids have only one pair of parallel sides; parallelograms have two pairs of parallel sides. A trapezoid can never be a parallelogram. The correct answer is that all trapezoids are quadrilaterals.
E. Rectangles: ___________
How do you know that a shape is a rectangle?
Answer: rectangle and parallelogram
* Yes, a rectangle is also a parallelogram, because it satisfies the conditions or meets the properties of parallelogram such as the opposite sides are parallel and diagonals bisect each other. Theorem 1: Parallelograms on the same base and between the same parallel sides are equal in area.
* A two-dimensional geometry having four sides whose opposite sides are equal and adjacent sides meet at 90° is called a rectangle. A rectangle is having two equal diagonals. The length of the diagonals is calculated by using their length and width.
When a rectangle has four right angles, all of the interior angles are congruent. The vertices join the adjacent sides at 90° angles, which means the opposite sides of the rectangle are parallel lines. Since it has two sets of parallel sides and two pairs of opposite sides that are congruent, a rectangle has all of the properties of a parallelogram. That’s why a rectangle is always a parallelogram.
Turn and Talk How would your answer in Part D change if a trapezoid is defined as having at least one pair of parallel sides?
Answer:
Question 2.
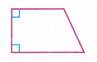
Circle the words that describe the shape.

Define a trapezoid as a quadrilateral that has at least one pair of parallel sides.
Answer: A trapezoid is a quadrilateral with at least one pair of parallel sides. These parallel sides are called bases.
– It can have right angles (a right trapezoid), and it can have congruent sides (isosceles), but those are not required.
– Sometimes people define trapezoids to have at least one pair of opposite sides parallel, and sometimes say there is one and only one pair of opposite sides parallel. The parallelogram fits the “at least one” version of the definition because it has two pairs of opposite sides parallel, therefore it falls into the category of being both a trapezoid and a parallelogram. The parallelogram does not fit the “one and only one” version of the definition. So how students answer this depends on their definition.
Turn and Talk Which shape belongs to the most categories? What attributes help to explain this?
Answer: Square shape
Square shape has more categories. They are quadrilaterals, parallelogram, rhombus, rectangle.
(i) a quadrilateral
Solution: A square is a quadrilateral, as it has four equal sides.
(ii) a parallelogram
Solution: A square is a parallelogram, as it contains the pairs of opposite sides equal.
(iii) a rhombus
Solution: A square is a rhombus, as it has four equal sides and diagonals bisect at 900.
(iv) a rectangle
Solution: A square is a rectangle, as it has each adjacent angle at 900 and opposite sides are equal.
Check Understanding
Circle the words that describe the shape. Define a trapezoid as a quadrilateral that has at least one pair of parallel sides.
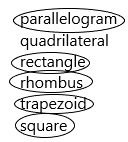
Question 1.
parallelogram
quadrilateral
rectangle
rhombus
trapezoid
square
Answer:
A quadrilateral is a plane figure that has four sides or edges, and also has four corners or vertices. The angles are present at the four vertices or corners of the quadrilateral. If ABCD is a quadrilateral then angles at the vertices are ∠A, ∠B, ∠C and ∠D. The sides of a quadrilateral are AB, BC, CD and DA. If we join the opposite vertices of the quadrilateral, we get the diagonals.
Quadrilaterals will typically be of standard shapes with four sides like rectangle, square, trapezoid, and kite or irregular.
here asked to define a trapezoid as a quadrilateral that has at least one pair of parallel sides.
A trapezoid is a quadrilateral with at least one pair of parallel sides. These parallel sides are called bases.
– It can have right angles (a right trapezoid), and it can have congruent sides (isosceles), but those are not required.
– Sometimes people define trapezoids to have at least one pair of opposite sides parallel, and sometimes say there is one and only one pair of opposite sides parallel. The parallelogram fits the “at least one” version of the definition because it has two pairs of opposite sides parallel, therefore it falls into the category of being both a trapezoid and a parallelogram. The parallelogram does not fit the “one and only one” version of the definition. So how students answer this depends on their definition.
Question 2.
parallelogram
quadrilateral
rectangle
rhombus
trapezoid
square
Answer:

– A rectangle is a quadrilateral in which all angles are right angles. A rectangle is a parallelogram, so its opposite sides are equal. The diagonals of a rectangle are equal and bisect each other.
– A rectangle is a quadrilateral with all of its angles being right angles. Because a rectangle is a parallelogram, its opposing sides are also equal. A rectangle’s diagonals are equal and bisect each other.
– It is possible for a square to be a rectangle, but it is impossible for a rectangle to be a square. In order to be a square, the shape must contain four straight sides with 90-degree angles that are all the same length. A rectangle has four straight sides with four right angles, but the sides can be different lengths. The opposite sides of a rectangle must be parallel with one another and feature equal lengths. This means the shape can be tall and skinny or short and fat. The sides on a square must all be parallel in comparison with one another.
Question 3.

parallelogram
quadrilateral
rectangle
rhombus
trapezoid
square
Answer:
– The main point of difference between the two is that sides of rectangles form 90 degrees while this is not the case with parallelograms. Thus, a rectangle can be called a parallelogram as it fulfils all the requirements of a parallelogram but a parallelogram cannot be called a rectangle.
– A parallelogram is a quadrilateral with opposite sides parallel.
– A rhombus has 4 equal sides and 2 pairs of opposite, equal angles. A parallelogram has 2 pairs of equal sides and 2 pairs of equal angles. A rhombus is a parallelogram but a parallelogram is not a rhombus usually.
– Yes, a parallelogram is a trapezium but a trapezium is not a parallelogram. This is true because a trapezium is a quadrilateral with one pair of opposite sides parallel and a parallelogram is a quadrilateral with one pair of sides parallel and equal.
– If the diagonals of a parallelogram are congruent and perpendicular, the parallelogram is a square.
On Your Own
Question 4.
Construct Arguments Explain why a rectangle is always a parallelogram, but a parallelogram is not always a rectangle.
Answer: A parallelogram is a four-sided geometrical figure whose opposite sides are parallel and equal. Whereas a rectangle is a special case of the parallelogram which has all its four angles as right angles.
A parallelogram is a four-sided polygon (a quadrilateral) with
• Two pairs of parallel and equal sides.
• Two pairs of opposite interior angles equal, and
• Adjacent angles being supplementary; add up to 180°.
• Diagonals bisect each other,
• Diagonals are unequal.
Rectangles possess all those properties of a parallelogram stated above. However, in addition, it has certain distinct attributes. They are,
• All interior angles are right angles (90°)
• Diagonals are equal.
That makes rectangles unique parallelograms. That differentiates rectangles from parallelograms. Parallelograms will fall short of those attributes to be a rectangle. Not every parallelogram is a rectangle.
Question 5.
Reason Is a square always a rectangle? How do you know?
Is a rectangle always a square? How do you know?
Answer: All squares are rectangles, but not all rectangles are squares.
The similarities in the properties of a square and a rectangle can help us draw a conclusion to the query “Is square a rectangle”. In Geometry, we have learned about different types of shapes such as square, rectangle, cylinder, rhombus, cuboid, cube, cone, parallelogram, and so on. Many of these shapes share certain common properties. Square and rectangle are examples of such two-dimensional shapes. They both fall under the category of quadrilaterals.
Square Vs Rectangle:
Square: A square is a two-dimensional plane figure with four equal sides, four interior right angles, and four corners. In other words, a square is a quadrilateral or a 4-sided polygon. All the angles are of equal measure, therefore it is considered as an equiangular quadrilateral.
Rectangle: A rectangle is a two-dimensional figure with four sides, four interior right angles, and four corners. The opposite sides of a rectangle are equal. A rectangle has four angles, with each angle measuring 90º. Similar to a square, a rectangle is also referred to as an equiangular quadrilateral.
Let us have a look at the image given here to understand a square and a rectangle better.
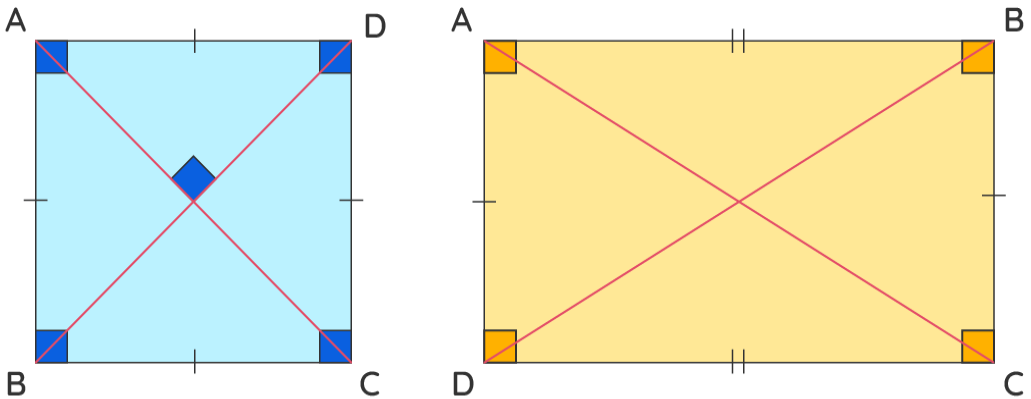
Since both a square and a rectangle have an equal number of sides, i.e., 4, we thus can conclude that both square and rectangle are quadrilaterals. We can observe the similarities in the properties of both a square and a rectangle in the following section.
Properties of square and rectangle:
Both a square and a rectangle have certain special properties that distinguish them from a general quadrilateral. We can draw the comparison of the requisite properties of both the shapes from the following table and conclude whether a square has all the properties that define a rectangle.
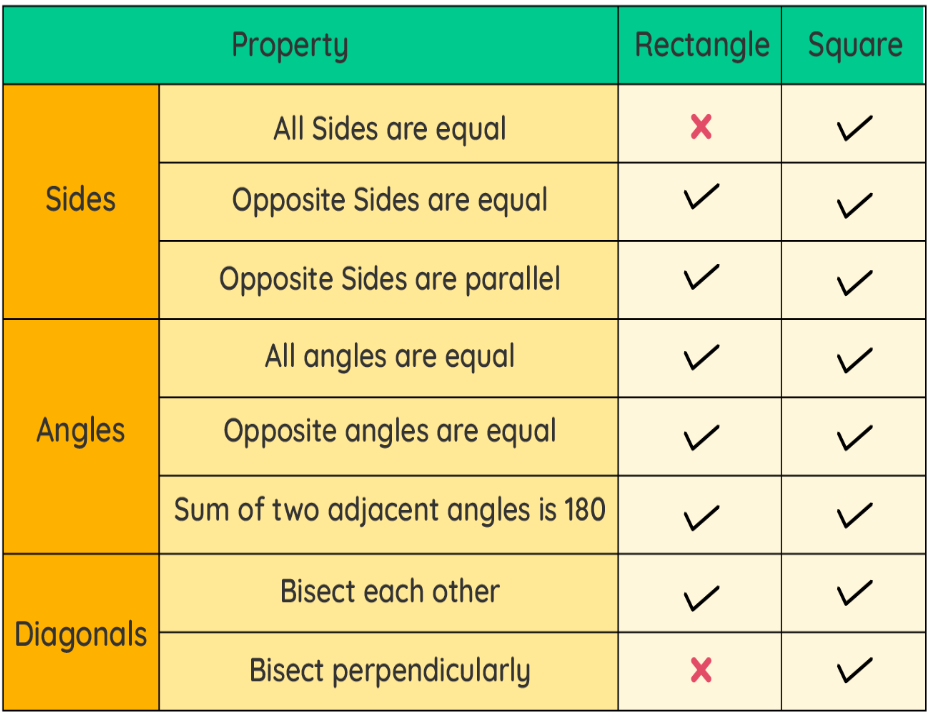
What are squares and rectangles be alike: From the comparison drawn above for the common properties shared between a square and a rectangle, we observe that a square has all the properties that define a rectangle, which makes them alike in a certain manner. This means that a square can also be referred to as a type of rectangle.
Thus, we can finally conclude that yes, a square is a rectangle.
– A rectangle is a quadrilateral with all four angles right angles. Thus every square is a rectangle because it is a quadrilateral with all four angles right angles. However not every rectangle is a square, to be a square its sides must have the same length.
Question 6.
STEM Crystals can form when liquid rock under Earth cools and hardens into a pattern. What quadrilateral best describes one of the crystal’s faces that has 4 sides of equal length and 2 pairs of parallel sides?

Answer: I would say it is a square with four equal sides.
Definition: Square is a regular quadrilateral, which has all four sides of equal length and all four angles are also equal. The angles of the square are at right-angle or equal to 90-degrees. Also, the diagonals of the square are equal and bisect each other at 90 degrees. A square can also be defined as a rectangle where two opposite sides have equal length.
Square
Number of sides = 4; Number of vertices = 4; Area = Side2; Perimeter = 4(Side)
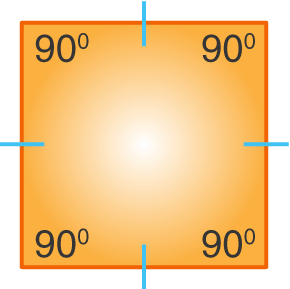
Properties of square:
The most important properties of a square are listed below:
– All four interior angles are equal to 90°
– All four sides of the square are congruent or equal to each other
– The opposite sides of the square are parallel to each other
– The diagonals of the square bisect each other at 90°
– The two diagonals of the square are equal to each other
– The square has 4 vertices and 4 sides
– The diagonal of the square divide it into two similar isosceles triangles
– The length of diagonals is greater than the sides of the square
Question 7.
Circle the shapes that are trapezoids when a trapezoid is defined as a quadrilateral that has exactly one pair of parallel sides.

Answer:
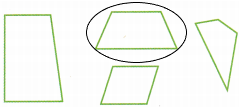
A trapezoid is a four-sided shape (quadrilateral) such that one pair of opposite sides are parallel. Some of the properties of trapezoids are: one pair of opposite sides are parallel, etc. A trapezoid is isosceles is one pair of opposite sides that are equal.
what are the rules for a trapezoid?
– The properties of trapezoid apply by definition (parallel bases).
– The legs are congruent by definition.
– The lower base angles are congruent.
– The upper base angles are congruent.
– Any lower base angle is supplementary to any upper base angle.
– The diagonals are congruent.
I’m in a Learning Mindset!
What do I do when I do not know how to classify a quadrilateral?
Answer: We can use the slopes and length concept to classify the quadrilaterals.