Engage NY Eureka Math Grade 6 Module 5 End of Module Assessment Answer Key
Eureka Math Grade 6 Module 5 End of Module Assessment Answer Key
Question 1.
The juice box pictured below is 4 inches high, 3 inches long, and 2 inches wide.
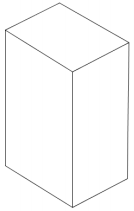

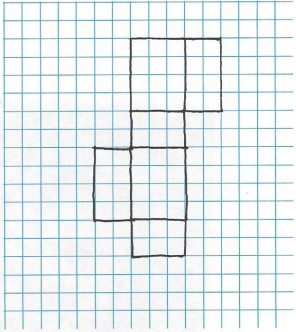
a. In the grid above, the distance between grid lines represents one inch. Use the grid paper to sketch the net of the juice box.
Answer:
b. Find the surface area of the juice box. Show your work.
Answer:
SA = 2(l.w + l.h + w.h)
SA = 2(3 in. . 2 in. + 3 in. . 4 in. + 2 in. . 4 in.)
SA = 2(6 in2 + 12 in2 + 8 in2)
SA = 2(26 in2)
SA = 52 in2
c. Find the volume of the juice box. Show your work.
Answer:
V = l.w.h
V = 3 in. . 2 in. . 4 in.
V = 24 in2
Question 2.
The Cubic Crystal Company has a new Crystal Cube they want to sell. The packaging manager insists that the cubes be arranged to form a rectangular prism and that the package be designed to hold the Crystal Cubes exactly, with no leftover packaging. Each Crystal Cube measures 1 in. × 1 in. × 1 in. There are 24 Crystal Cubes to be sold in a box.
a. What are the dimensions of the possible box designs in inches?

Answer:
| Height | Width | Length |
| 1 in | 1 in | 24 in |
| 1 in | 2 in | 12 in |
| 1 in | 3 in | 8 in |
| 1 in | 4 in | 6 in |
| 2 in | 2 in | 6 in |
| 2 in | 3 in | 4 in |
b. Which Crystal Cube box design will use the least amount of cardboard for packaging? Justify your answer as completely as you can.

Answer:
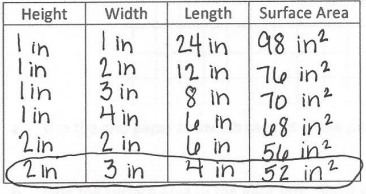
The minimum surface area is found to be on the 2 in × 3 in × 4 in box. That box needs the least amount of cardboard.
c. Another type of cube is the Mini Crystal Cube, which has an edge length of inch. What is the volume in cubic inches of one Mini Crystal Cube? Show your work.
Answer:
V = l.w.h
V = \(\frac{3}{4}\) in . \(\frac{3}{4}\) in . \(\frac{3}{4}\) in
V = \(\frac{27}{64}\) in3
Question 3.
Which of these nets can be folded to form a cube?

Answer:

Question 4.
Which box below has the larger surface area?
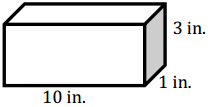
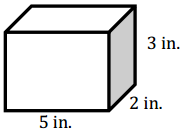
Answer:
SA = 2(l.w + l.h + w.h)
SA = 2(5 in. . 2 in. + 5 in. . 3in. + 2 in. . 3 in.)
SA = 2(10 in2. + 15 in2. + 6 in2.)
SA = 2(31 in2.)
SA = 62 in2.
SA = 2(l.w + l.h + w.h)
SA = 2(10 in. . 1 in. + 10 in. 3 in. + 1 in. . 3 in.)
SA = 2(10 in2 + 30 in2. + 3 in2.)
SA = 2(43 in2.)
SA = 86 in2
This box has the larger surface area.
Question 5.
a. Draw a polygon in the coordinate plane using the given coordinates.

(4, -4)
(6, -2)
(8, -6)
Answer:

b. Calculate the area of the polygon.
Answer:
Area of Square:
A = l.w or S2
A = 4 u. 4 u or (4 u)2
A = 16 u2
Area of Triangle 1:
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) 2 u . 2u
A = 2 u2
Area of Triangle 2:
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) 2 u . 4 u
A = 4 u2
Area of Triangle 3:
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) . 2 u . 4 u
A = 4 u2
Area of Triangle 4 = 16 u2 – 2 u2 – 4 u2 – 4 u2 = 6 u2
Question 6.
Eaglecrest Elementary School is creating a vegetable garden at the school.
a. What is the area of the garden?

Answer:
A = b.h
A = 25 ft . 6 ft
A = 150 ft2
b. After more discussion, Eaglecrest decided to change the location of the garden so that the vegetables can get more sunlight. Below is the new garden.

In which garden can eagle crest students plant more vegetables? Explain your reasoning.
Answer:
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\)(7 ft. . 28 ft.)
A = \(\frac{1}{2}\) (194 ft2)
A = 98 ft2
The students of Eaglecrest can plant more vegetables in original garden in the shape of a parallelogram. It has a larger area than the triangular prism.