Engage NY Eureka Math Grade 6 Module 5 Mid Module Assessment Answer Key
Eureka Math Grade 6 Module 5 Mid Module Assessment Answer Key
Question 1.
David is the groundskeeper at Triangle Park, scale shown below.
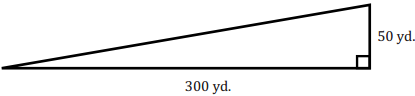
Answer:
a. David needs to cut the grass four times a month. How many square yards of grass will he cut altogether each month?
Answer:
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) 300yd. 50yd
A = \(\frac{1}{2}\) . 15,000 yd2
A = 7,500 yd2
4 . 7,500 yd2 = 30,000 yd2
b. During the winter the triangular park and adjacent square parking lot are flooded with water and allowed to freeze so that people can go ice skating. What is the area of the ice?
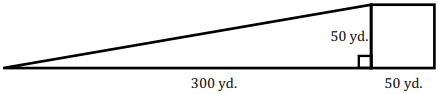
Answer:
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) . 300yd. 50 yd
A = \(\frac{1}{2}\) . 15,000 yd2
A = 7,500 yd2
A = S2
A = (50 yd)2
A = 2,500 yd2
7,500 yd2 + 2,500 yd2 = 10,000 yd2
Question 2.
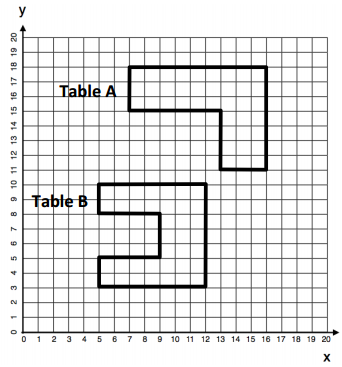
Mariska is looking for a new computer table. Below is a sketch of two computer tables she likes when looking at them from above. All measurements are in feet.
a. If Mariska needs to choose the one with the greater area, which one should she choose? Justify your answer with evidence, using coordinates to determine side lengths.
Answer:
Table A:
(7, 15) → (7, 18) = 3 ft.
(7, 18) → (16, 18) = 9 ft.
(16, 18) → (16, 11) = 7 ft.
(16, 11) → (13, 11) = 3 ft.
(13, 11) → (13, 15) = 4 ft.
(13, 15) → (7, 15) = 6 ft.
A = bh
A = 9 ft. . 3 ft.
A = 27 ft2
A = bh
A = 3 ft. . 4 ft.
A = 12 ft2
27 ft2 + 12 ft2 = 39 ft2
Table B:
(5, 8) → (5, 10) = 2 ft.
(5, 10) → (2, 10) = 7 ft.
(12, 10) → (12, 3) = 7 ft.
(12, 3) → (5, 3) = 7 ft.
(5, 3) → (5, 5) = 2 ft.
(5, 5) → (9, 5) = 4 ft.
(9, 5) → (9, 8) = 3 ft.
(9, 8) → (5, 8) = 4 ft.
A = bh
A = 7 ft. . 2 ft.
A = 14 ft2
A = bh
A = 3 ft. 3 ft
A = 9 ft2
A = bh
A = 7 ft. . 2 ft
A = 14 ft2
14 ft2 + 9 ft2 + 14 ft2 = 37 ft2
Mariska will need to choose Table A because it is the table with the greatest area
b. If Mariska needs to choose the one with the greater perimeter, which one should she choose? Justify your answer with evidence, using coordinates to determine side lengths.
Answer:
Table A:
P = 3 ft. + 9 ft. + 7 ft. + 3 ft. + 4 ft. + 6 ft.
P = 32 ft.
Table B:
P = 2 ft. + 7 ft. + 7 ft. + 7 ft. + 2 ft. + 3 ft. + 4 ft. + 4 ft.
P = 36 ft.
Table B has a large perimeter.
Question 3.
Find the area of the triangular region.
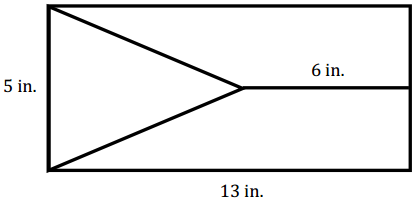
Answer:
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) . 5 in. 7 in.
A = \(\frac{1}{2}\) . 35 in2
A = 17.5 in2
Question 4.
The grid below shows a bird’s-eye view of a middle school.
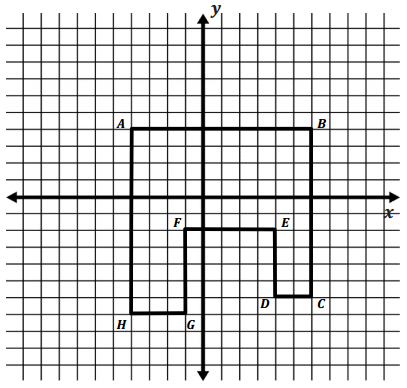
a. Write the coordinates of each point in the table.
Answer:
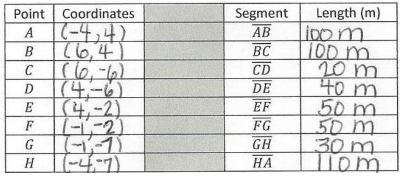
b. Each space on the grid stands for 10 meters. Find the length of each wall of the school.
Answer:
c. Find the area of the entire building. Show your work.
Answer:
A = bh
A = 100 m . 60 m
A = 6,000 m2
A = bh
A = 30 m . 50 m
A = 1,500 m2
A = bh
A = 20 m . 40 m
A = 800 m2
6,000 m2 + 1,500 m2 + 800 m2 = 8,300 m2