The solutions to Bridges in Mathematics Grade 3 Home Connections Answer Key Unit 4 Module 3 can help students to clear their doubts quickly.
Bridges in Mathematics Grade 3 Home Connections Answer Key Unit 4 Module 3
Bridges in Mathematics Grade 3 Home Connections Unit 4 Module 3 Session 1 Answer Key
Sharing Candy Bars & Measuring
Question 1.
You are sharing a candy bar with friends.
a. If you share with one person, there are two of you sharing. How do you write your share?
Answer:
Share of the candy each person gets = \(\frac{1}{2}\).
Explanation:
Number of persons to share candy = 2.
Number of candies = 1.
Share of the candy each person gets = Number of persons to share candy ÷ Number of candies
= 1 ÷ 2
= \(\frac{1}{2}\).
b. If you share with two people, there are three of you sharing. How do you write your share?
Answer:
Share of the candy each person gets = \(\frac{1}{3}\).
Explanation:
Number of persons to share candy = 3.
Number of candies = 1
Share of the candy each person gets = Number of persons to share candy ÷ Number of candies
= 1 ÷ 3
= \(\frac{1}{3}\).
c. Would you have more candy if you share with one person or two people? Explain your answer.
Answer:
If I have more candy and people increase there will be increase in the share of each person.
Explanation:
If,
a. Number of persons to share candy = 2.
Number of candies = 3.
Share of the candy each person gets = Number of persons to share candy ÷ Number of candies
= 2 ÷ 3
= \(\frac{2}{3}\).
b. Number of persons to share candy = 7.
Number of candies = 5.
Share of the candy each person gets = Number of persons to share candy ÷ Number of candies
= 5 ÷ 7
= \(\frac{5}{7}\).
Question 2.
Circle the appropriate words to fill in the blanks.
a. A bowling ball is heavy! I would measure its ____ with _____.
![]()
Answer:

Explanation:
A bowling ball is heavy!
I would measure its mass with kilograms.
b. A sun jellyfish is pretty long. I would measure its ___ with ____.
![]()
Answer:

Explanation:
A sun jellyfish is pretty long.
I would measure its length with centimeters.
c. A water bottle doesn’t hold much. I would measure its ____ with ____.
![]()
Answer:

Explanation:
A water bottle doesn’t hold much.
I would measure its mass with liters.
d. A giraffe is tall. I would measure its ____ with ____.
![]()
Answer:

Explanation:
A giraffe is tall.
I would measure its height with meters.
e. An elephant eats lots! I would measure the ____ of its food with ____.
![]()
Answer:

Explanation:
An elephant eats lots!
I would measure the mass of its food with kilograms.
f. An Etruscan shrew is short. I would measure its ____ with ____.
![]()
Answer:

Explanation:
An Etruscan shrew is short.
I would measure its length with centimeters.
g. An Etruscan shrew is light. I would measure its ____ with ____.
![]()
Answer:

Explanation:
An Etruscan shrew is light.
I would measure its mass with grams.
h. That bucket holds a lot! I would measure its ____ with ____.
![]()
Answer:

Explanation:
That bucket holds a lot!
I would measure its volume with liters.
Show all your thinking with numbers, words, or sketches for each of the problems below. Label your answers with the correct units.
Question 3.
A bottle of Charlie’s favorite brand of orange juice has 7 servings. Each serving is 240 milliliters (ml).
a. How many milliliters of orange juice are in the whole bottle?
Answer:
Total number of milliliters of orange juice are in the whole bottle = 1,680.
Explanation:
Number of servings a bottle of Charlie’s favorite brand of orange juice has = 7.
Number of milliliters each serving = 240.
Total number of milliliters of orange juice are in the whole bottle = Number of servings a bottle of Charlie’s favorite brand of orange juice has × Number of milliliters each serving
= 7 × 240
= 1,680.
b. Is that more or less than 2 liters? (Hint: 1 liter = 1,000 milliliters)
Answer:
Total number of milliliters of orange juice are in the whole bottle is less than 2 liters.
Explanation:
Total number of milliliters of orange juice are in the whole bottle = 1,680.
Conversion:
1 liter = 1,000 milliliters
?? liter = 1,680 milliliters
=> 1 × 1680 = ?? × 1000
=> 1,680 ÷ 1000 = ??
=> 1.680 liters = ??
Question 4.
CHALLENGE A box of soup contains 4 servings. Each serving has 4\(\frac{1}{2}\) grams of fat and 720 milligrams of sodium.
a. If someone was really hungry and ate all 4 servings in the box, how many grams of fat would that person eat?
Answer:
Number of grams of fat that person ate = 18.
Explanation:
Number of servings a box of soup contains = 4.
Number of grams of fat each serving has = 4\(\frac{1}{2}\).
Number of milligrams of sodium each serving has = 720.
Number of servings in the box someone was really hungry and ate = 4.
Number of grams of fat that person ate = Number of servings a box of soup contains × Number of grams of fat each serving has
= 4 × 4\(\frac{1}{2}\).
= 4 × {[(4 × 2) + 1] ÷ 2}
= 4 × [(8 + 1) ÷ 2]
= 4 × (9 ÷ 2)
= 2 × (9 ÷ 1)
= 18 ÷ 1
= 18.
b. How many milligrams (mg) of sodium would that person eat?
(1 gram = 1,000 milligrams)
Answer:
Number of milligrams of sodium that person ate = 2,880.
Explanation:
Number of servings a box of soup contains = 4.
Number of grams of fat each serving has = 4\(\frac{1}{2}\).
Number of milligrams of sodium each serving has = 720.
Number of servings in the box someone was really hungry and ate = 4.
Number of milligrams of sodium that person ate = Number of servings a box of soup contains × Number of milligrams of sodium each serving has
= 4 × 720
= 2,880.
Conversion:
1 gram = 1,000 milligrams
c. It is recommended that people eat no more than 2,400 mg of sodium in a day. If a person ate a whole box of the soup, would that person take in more or less than 2,400 mg?
Answer:
He ate more of sodium in a day than 2,400 mg.
Explanation:
Number of milligrams of sodium in a day that people eat no more than = 2,400.
Number of servings a box of soup contains = 4.
Number of grams of fat each serving has = 4\(\frac{1}{2}\).
Number of milligrams of sodium each serving has = 720.
Number of servings in the box someone was really hungry and ate = 4.
Number of milligrams of sodium that person ate = Number of servings a box of soup contains × Number of milligrams of sodium each serving has
= 4 × 720
= 2,880.
Difference:
Number of milligrams of sodium that person ate – Number of milligrams of sodium in a day that people eat no more than
= 2880 – 2400
= 480 milligrams.
d. How many milligrams more or less?
Answer:
He ate 480 milligrams of sodium more than 2,400 milligrams.
Explanation:
Number of milligrams of sodium in a day that people eat no more than = 2,400.
Number of servings a box of soup contains = 4.
Number of grams of fat each serving has = 4\(\frac{1}{2}\).
Number of milligrams of sodium each serving has = 720.
Number of servings in the box someone was really hungry and ate = 4.
Number of milligrams of sodium that person ate = Number of servings a box of soup contains × Number of milligrams of sodium each serving has
= 4 × 720
= 2,880.
Difference:
Number of milligrams of sodium that person ate – Number of milligrams of sodium in a day that people eat no more than
= 2880 – 2400
= 480 milligrams.
Bridges in Mathematics Grade 3 Home Connections Unit 4 Module 3 Session 3 Answer Key
Measurement & Fractions
Question 1.
Circle the appropriate words to fill in the blank.
a A piece of paper is light! I would measure its ____________ with ______.
![]()
Answer:

Explanation:
A piece of paper is light!
I would measure its Mass with grams.
b. That pencil is short! I would measure its ___________ with ____.
![]()
Answer:

Explanation:
That pencil is short!
I would measure its Length with centimeters.
c. A soda can doesn’t hold very much. I would measure its ______ with ___.
![]()
Answer:

Explanation:
A soda can doesn’t hold very much.
I would measure its mass with milliliters.
Question 2.
Circle your answer.
a. Which is longer—half of a day or half of an hour?
Answer:
Longer is:

Explanation:
Conversion:
a. 1 day – 24 hours.
=> half of a day = 24 ÷ 2 = 12 hours.
1 hour – 60 minutes.
=> half of an hour = 60 ÷ 2 = 30 minutes.
=> 12 hours = 60 × 12 = 720 minutes.
Therefore, 720 minutes is longer than 30 minutes.
b. Which is heavier—half of a gram or half of a kilogram?
Answer:
Heavier is:
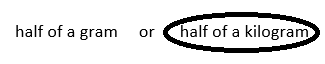
Explanation:
Conversion:
1 kilogram = 1000 grams.
=> half of a gram = 1 ÷ 2 = \(\frac{1}{2}\) gram.
=> half of a kilogram = 1000 ÷ 2 = 500 grams.
c. Which holds more—half of a milliliter or half of a liter?
Answer:

Explanation:
Conversion:
1 liter = 1000 milliliters.
=> half of a milliliter = 1 ÷ 2 = \(\frac{1}{2}\) milliliter.
=> half of a liter = 1000 ÷ 2 = 500 milliliters.
Question 3.
Write the correct symbol: < or > or =
\(\frac{1}{4}\) ![]() \(\frac{1}{10}\) \(\frac{1}{4}\)
\(\frac{1}{10}\) \(\frac{1}{4}\) ![]() \(\frac{1}{2}\) \(\frac{1}{4}\)
\(\frac{1}{2}\) \(\frac{1}{4}\) ![]() 1
1
Answer:
\(\frac{1}{4}\) > \(\frac{1}{10}\).
\(\frac{1}{4}\) < \(\frac{1}{2}\).
\(\frac{1}{4}\) < 1.
Explanation:
\(\frac{1}{4}\) \(\frac{1}{10}\)
=> 0.25 > 0.10.
=> \(\frac{1}{4}\) is greater than \(\frac{1}{10}\).
\(\frac{1}{4}\) \(\frac{1}{2}\)
=> 0.25 < 0.50.
=> \(\frac{1}{4}\) is lesser than \(\frac{1}{2}\).
\(\frac{1}{4}\) 1
=> 0.25 < 1.
=> \(\frac{1}{4}\) is lesser than 1.
Question 4.
Choose one pair of fractions from problem 3. Discuss your answer. How do you know that one of the numbers is more than the other?
Answer:
We get to know that one of the numbers is more than the other by checking the place value of the digits.
Explanation:
\(\frac{1}{4}\) \(\frac{1}{10}\)
=> 0.25 > 0.10.
=> \(\frac{1}{4}\) is greater than \(\frac{1}{10}\).
In this problem, we get to know that 0.25 is greater than 0.10 by checking its place values.
Question 5.
Divide the shape into the number of parts you need, and shade in the fraction \(\frac{1}{3}\).
Answer:
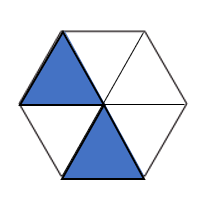
Explanation:
Given shade in the fraction = \(\frac{1}{3}\).
Number of parts I divided the figure = 6.
Number of parts I have shaded = 2.
Fraction I have shaded = Number of parts I have shaded ÷ Number of parts I divided the figure
= 2 ÷ 6
= \(\frac{1}{3}\).
Question 6.
My friends and I are sharing a candy bar. I got \(\frac{1}{4}\) of the candy bar, and my friend Abby got \(\frac{1}{4}\) of it. How much is left? Explain your answer.
Answer:
Portion of a candy bar left = \(\frac{1}{2}\).
Explanation:
Number of people sharing a candy bar = 4.
Fraction of the candy bar I got = \(\frac{1}{4}\).
Fraction of the candy bar my friend Abby got = \(\frac{1}{4}\).
Portion of a candy bar left = 1 – (Fraction of the candy bar I got + Fraction of the candy bar my friend Abby got)
= 1 – ( \(\frac{1}{4}\) + \(\frac{1}{4}\))
= 1 – ( \(\frac{1+1}{4}\))
= 1 – \(\frac{2}{4}\)
= (4 – 2) ÷ 4
= \(\frac{2}{4}\)
= \(\frac{1}{2}\).
Question 7.
Tam filled his wading pool with 150 liters of water. Then 138 liters splashed out. How many liters are still in the pool? Write and solve an equation to represent the problem.
Answer:
Number of liters of water are still in the pool = 12.
Explanation:
Number of liters of water Tam filled his wading pool = 150.
Number of liters of water Tam splashed out = 138.
Number of liters of water are still in the pool = Number of liters of water Tam filled his wading pool – Number of liters of water Tam splashed out
= 150 – 138
= 12.
Question 8.
A bottle of Lilly’s favorite soda contains 590 milliliters of soda, has 260 calories, and 70 grams of carbohydrates. Lilly is going to share the bottle with Maddy, so each will get half the bottle. Show your work. Include the unit of measurement in your answer.
a. How many milliliters of soda will Lilly drink?
Answer:
Number of milliliters of soda Lilly drinks = 295.
Explanation:
Number of milliliters of soda a bottle of Lilly’s favorite soda contains = 590.
Number of calories a bottle of Lilly’s favorite soda contains = 260.
Number of grams of carbohydrates a bottle of Lilly’s favorite soda contains = 70.
Lilly is going to share the bottle with Maddy, so each will get half the bottle.
=> Number of milliliters of soda Lilly drinks = Number of milliliters of soda a bottle of Lilly’s favorite soda contains ÷ 2
= 590 ÷ 2
= 295.
b. How many calories will Maddy get?
Answer:
Number of calories Maddy gets = 130.
Explanation:
Number of milliliters of soda a bottle of Lilly’s favorite soda contains = 590.
Number of calories a bottle of Lilly’s favorite soda contains = 260.
Number of grams of carbohydrates a bottle of Lilly’s favorite soda contains = 70.
Lilly is going to share the bottle with Maddy, so each will get half the bottle.
=> Number of calories Maddy gets = Number of calories a bottle of Lilly’s favorite soda contains ÷ 2
= 260 ÷ 2
= 130.
c. How many grams of carbohydrates will each girl get?
Answer:
Number grams of carbohydrates each girl gets = 35.
Explanation:
Number of milliliters of soda a bottle of Lilly’s favorite soda contains = 590.
Number of calories a bottle of Lilly’s favorite soda contains = 260.
Number of grams of carbohydrates a bottle of Lilly’s favorite soda contains = 70.
Lilly is going to share the bottle with Maddy, so each will get half the bottle.
=> Number grams of carbohydrates each girl gets = Number of grams of carbohydrates a bottle of Lilly’s favorite soda contains ÷ 2
= 70 ÷ 2
= 35.
Use a separate sheet of paper to show your thinking using words, sketches, or numbers to solve the problems below.
Question 9.
CHALLENGE Chris is looking at a map to see how many miles it is from Golden Valley, where he lives, to Willow Lake, where his grandmother lives. The map uses a scale where 1\(\frac{1}{2}\) inches represents 12 miles.
a. Chris measured the map distance between the two towns and found that it is 6 inches. How many miles is it from Golden Valley to Willow Lake?
Answer:
Number of miles is it from Golden Valley to Willow Lake = 48 miles.
Explanation:
Given scale: 1\(\frac{1}{2}\) inches represents 12 miles.
=> \(\frac{3}{2}\) inches represents 12 miles.
=> 1.5 inches represents 12 miles.
Number of inches Chris measured the map distance between the two towns = 6.
Number of miles is it from Golden Valley to Willow Lake = Number of inches Chris measured the map distance between the two towns
=> 6
=> 1.5 + 1.5 + 1.5 + 1.5
=> 12 miles + 12 miles + 12 miles + 12 miles
=> 24 miles + 12 miles + 12 miles
=> 36 miles + 12 miles
=> 48 miles.
b. Chris will take the train to Willow Lake. The train goes 60 miles an hour. If Chris takes the 2:20 train, about what time will he get to Willow Lake?
Answer:
Correct time he reaches Willow Lake = 3.08.
Explanation:
Number of miles is it from Golden Valley to Willow Lake = 48 miles.
Speed of the train Chris goes = 60 miles an hour.
Time he takes the train = 2:20.
=> Number of miles is it from Golden Valley to Willow Lake ÷ Speed of the train Chris goes
=> 48 ÷ 60
=> 0.80.
Time interval it takes him to Willow Lake = Speed of the train Chris goes × 0.80
= 60 × 0.80
= 48 minutes.
Correct time he reaches Willow Lake = Time he takes the train + Time interval it takes him to Willow Lake
= 2:20 + 48
= 2.20 + 40 + 8
= 3.00 + 8
= 3.08.
Bridges in Mathematics Grade 3 Home Connections Unit 4 Module 3 Session 5 Answer Key
Fractions, Fractions & Fractions
Question 1.
Complete the missing information below by writing in the fraction number or sketching the given fraction on a number line.
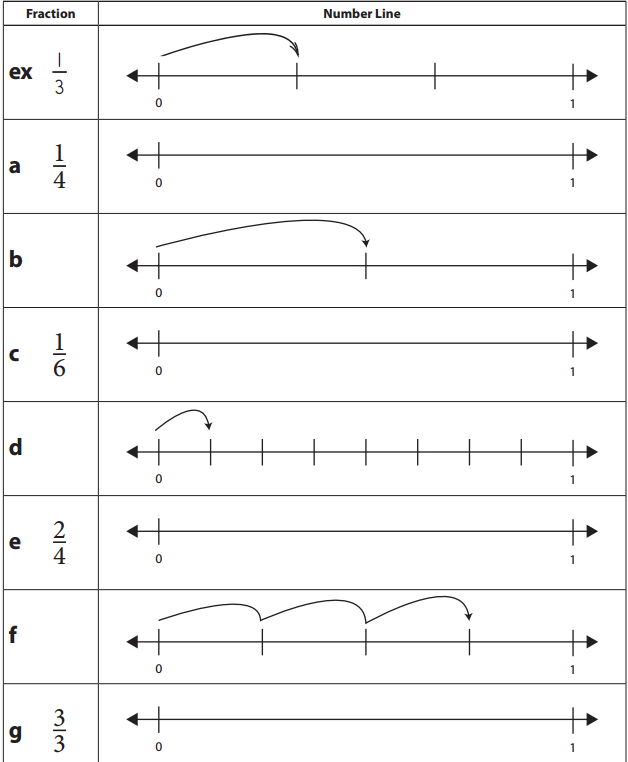
Answer:
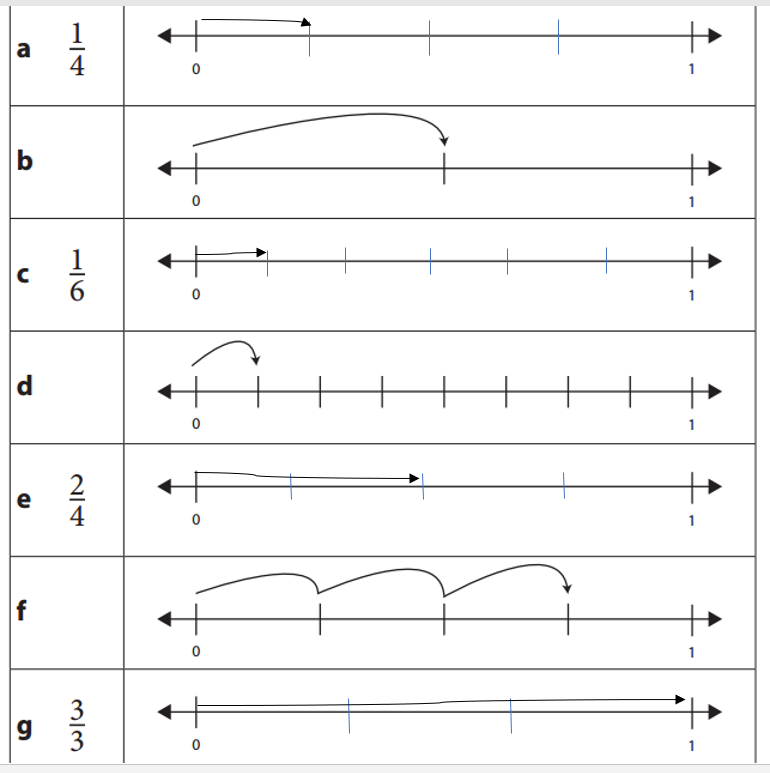
Explanation:
a. \(\frac{1}{4}\)
=> Total parts – 4 Fraction to show – 1
b. \(\frac{1}{2}\)
=> Total parts – 2 Fraction showed – 1
c. \(\frac{1}{6}\)
=> Total parts – 6 Fraction to show – 1
d. \(\frac{1}{8}\)
=> Total parts – 8 Fraction showed – 1
e. \(\frac{2}{4}\)
=> Total parts – 4 Fraction to show – 2
f. \(\frac{3}{4}\)
=> Total parts – 4 Fraction showed – 3
g. \(\frac{3}{3}\)
=> Total parts – 3 Fraction to show – 3
Question 2.
Use a < (less than), > (greater than) or = (equal) symbol to compare the following fraction pairs. Show your thinking by placing the fractions on the number line.
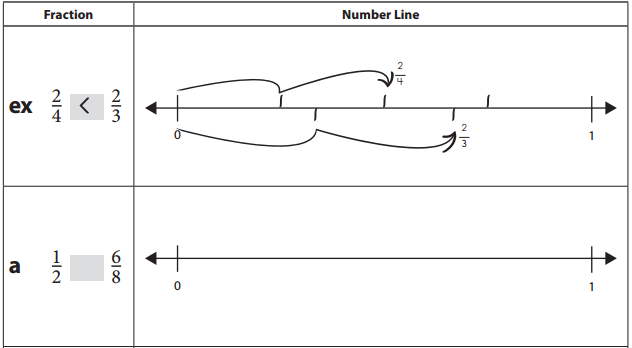
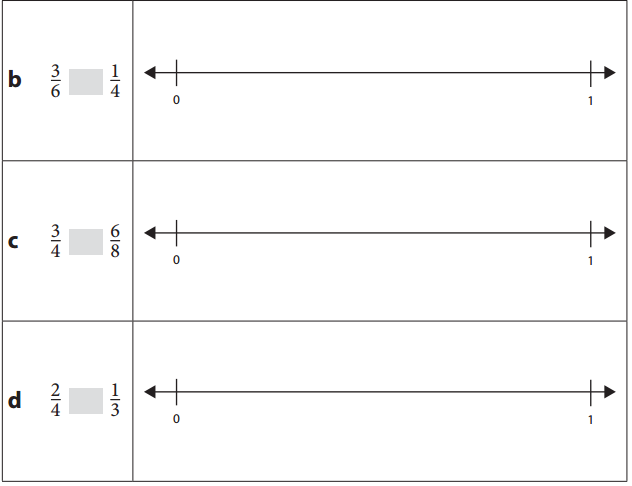
Answer:
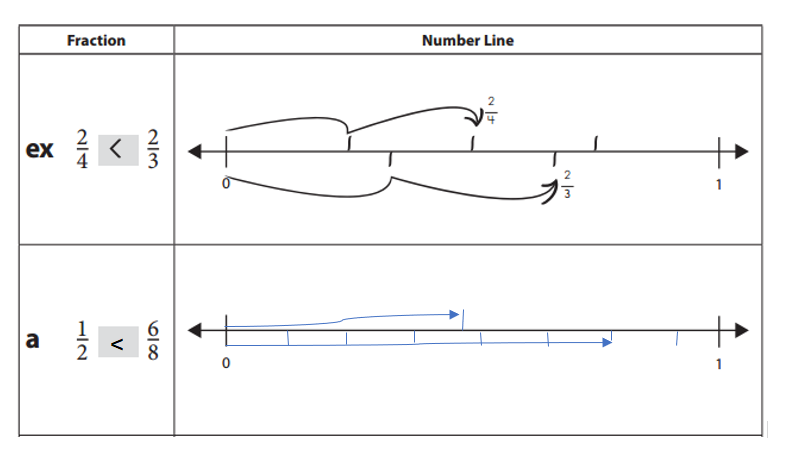
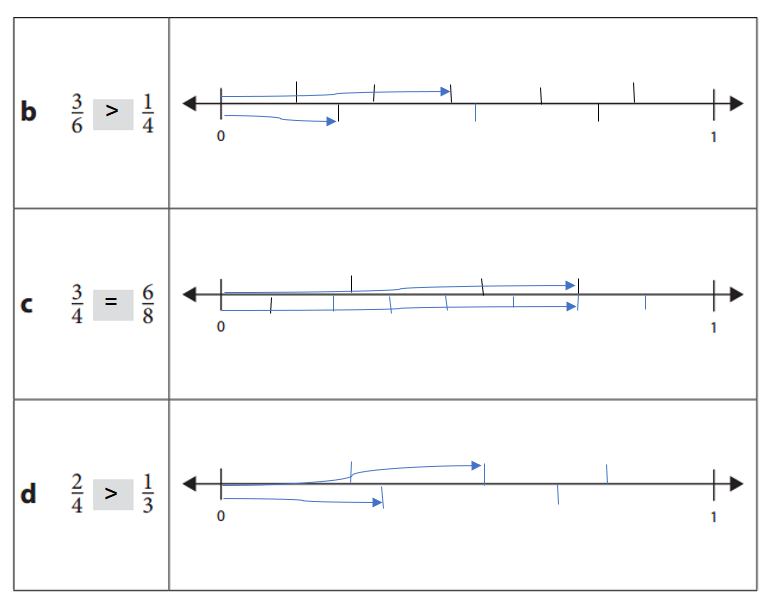
Explanation:
a. \(\frac{1}{2}\) is lesser than \(\frac{6}{8}\).
=> \(\frac{1}{2}\) = 0.5.
\(\frac{6}{8}\) = \(\frac{3}{4}\) = 0.75
b. \(\frac{3}{6}\) is greater than \(\frac{1}{4}\).
=> \(\frac{3}{6}\) = \(\frac{1}{2}\) = 0.5.
\(\frac{1}{4}\) = 0.25.
c. \(\frac{3}{4}\) is equal to \(\frac{6}{8}\).
=> \(\frac{3}{4}\) = 0.75.
\(\frac{6}{8}\) = \(\frac{3}{4}\) = 0.75.
d. \(\frac{2}{4}\) is greater than \(\frac{1}{3}\).
=> \(\frac{2}{4}\) = \(\frac{1}{2}\) = 0.50.
\(\frac{1}{3}\) = 0.33.