The solutions to Bridges in Mathematics Grade 3 Home Connections Answer Key Unit 4 Module 4 can help students to clear their doubts quickly.
Bridges in Mathematics Grade 3 Home Connections Answer Key Unit 4 Module 4
Bridges in Mathematics Grade 3 Home Connections Unit 4 Module 4 Session 2 Answer Key
Snack Time: Mass, Volume & Length
Question 1.
Use numbers, words, or sketches to show your thinking for problems a, b, and c. Don’t forget to include the unit of measurement in your answers.
a. Carl ate an apple that had a mass of 184 grams. Then, he ate 196 grams of peanuts. What was the total mass of Carl’s snack?
Answer:
The total mass of Carl’s snack = 380 grams.
Explanation:
Number of grams of an apple Carl ate = 184.
Number of grams of peanuts Carl ate = 196.
The total mass of Carl’s snack = Number of grams of an apple Carl ate + Number of grams of peanuts Carl ate
= 184 + 196
= 380 grams.
b. Allegra drank 203 milliliters of water. Then, she drank 157 milliliters of lemonade. How many milliliters of liquid did Allegra drink in all?
Answer:
Total number of milliliters of liquid Allegra drinks in all = 360.
Explanation:
Number of milliliters of water Allegra drank = 203.
Number of milliliters of lemonade Allegra drank = 157.
Total number of milliliters of liquid Allegra drinks in all = Number of milliliters of water Allegra drank + Number of milliliters of lemonade Allegra drank
= 203 + 157
= 360.
c. Mr. Alcott’s class was eating licorice twists for a special treat. They ate 117 feet of licorice twists. Mrs. Austen’s class was also eating licorice twists. They ate 79 feet of licorice twists. How many more feet of licorice twists did Mr. Alcott’s class eat?
Answer:
38 more feet of licorice twists Mr. Alcott’s class ate.
Explanation:
Number of feet of licorice twists Mr. Alcott’s class ate = 117.
Number of feet of licorice twists Mrs. Austen’s class ate = 79.
Difference:
Number of feet of licorice twists Mr. Alcott’s class ate – Number of feet of licorice twists Mrs. Austen’s class ate
= 117 – 79
= 38.
Question 2.
What unit do you use? Circle the unit you would use for each type of measurement.

Answer:

Explanation:
Units used for the Measurement of:
Length – Centimeters.
Mass – Grams.
Volume – Meters.
Use numbers, words, or sketches to show your thinking for all these problems. Don’t forget to include the unit of measurement in your answers.
Question 3.
Mike has a can of potato chips. There are 16 chips in one serving, and one serving weighs 28 grams.
a. How many grams do 3 servings weigh?
Answer:
84 grams 3 servings weigh.
Explanation:
Number of chips in one serving = 16.
Number of grams in one serving = 28.
Number of grams in 3 servings = 3 × Number of grams in one serving
= 3 × 28
= 84.
b. One serving of the potato chips has 150 calories. How many calories are in 3 servings?
Answer:
Number of calories three serving of the potato chips has = 450.
Explanation:
Number of chips in one serving = 16.
Number of grams in one serving = 28.
Number of calories one serving of the potato chips has = 150.
Number of calories three serving of the potato chips has = 3 × Number of calories one serving of the potato chips has
= 3 × 150
= 450.
c. One serving of the potato chips has 160 milligrams of sodium. How many milligrams of sodium are in 3 servings?
Answer:
Number of milligrams of sodium three serving of the potato chips has = 480.
Explanation:
Number of milligrams of sodium one serving of the potato chips has = 160.
Number of milligrams of sodium three serving of the potato chips has = 3 × Number of milligrams of sodium one serving of the potato chips has
= 3 × 160
= 480.
Question 4.
One can of potato chips has 5 servings. Each serving has 15 grams of carbohydrates.
a. How many grams of carbohydrates are in a whole can of potato chips?
Answer:
75 grams of carbohydrates are in a whole can of potato chips.
Explanation:
Number of servings One can of potato chips has = 5.
Number of grams of carbohydrates each serving has = 15.
Number of grams of carbohydrates are in a whole can of potato chips = Number of grams of carbohydrates each serving has × 5
= 15 × 5
= 75.
b. CHALLENGE How many cans of potato chips are needed for 14 people to each have 3 servings?
Answer:
Number of cans of potato chips are needed for 14 people = 9.
Explanation:
Number of servings one can of potato chips has = 5.
Number of grams of carbohydrates each serving has = 15.
Number of people = 14.
Number of servings each person has = 3.
Total number of servings 14 people have = Number of people × Number of servings each person has
= 14 × 3
= 42.
Number of cans of potato chips are needed for 14 people = Total number of servings 14 people have ÷ Number of servings one can of potato chips has
= 42 ÷ 5
= 8 quotient 2 remainder.
= 9.
Bridges in Mathematics Grade 3 Home Connections Unit 4 Module 4 Session 3 Answer Key
Time & Fraction Review
Question 1.
Fill in the circle next to the time shown on each clock.
a.
![]() 1:45
1:45
![]() 1:47
1:47
![]() 2:47
2:47
![]() 9:09
9:09

Answer:


Explanation:
Hours hand pointing: 9 and 10 in between.
Minutes hand pointing: 9.
Time shown: 9:09.
b.
![]() 3:40
3:40
![]() 8:04
8:04
![]() 8:19
8:19
![]() 8:20
8:20

Answer:


Explanation:
Hours hand pointing: 8 and 9 in between.
Minutes hand pointing: 4.
Time shown: 8:20.
Question 2.
Write the time shown on each clock.
a _____ : _____

Answer:
Time shown in the clock is 4:28.
Explanation:
Hours hand pointing: 4 and 5 in between.
Minutes hand pointing: 28.
Time shown: 4:28.

b. ____ : _____

Answer:
Time shown in the clock is 11:50.
Explanation:
Hours hand pointing: 10 and 11 in between.
Minutes hand pointing: 10.
Time shown: 11:50.
Question 3.
Circle the digital clock that shows the same time as this analog clock.
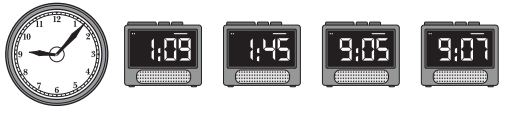
Answer:
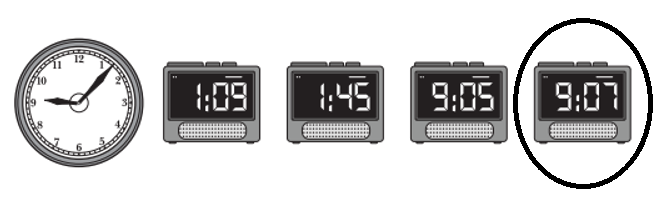
Explanation:
Hours hand pointing: 9.
Minutes hand pointing: 07.
Time shown: 9:07.
Question 4.
Taylor’s mom said he and his brother could go to a movie while she went shopping. She dropped them off at the theater at 1:45 and said she would be back at 4:00 to get them. They had three choices of movies. Which movie could they see and be done by the time their mom came to get them? Show all your work. Hint: Remember that there are 60 minutes in an hour.
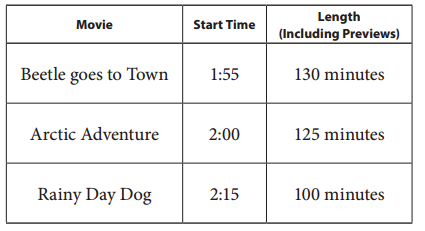
Answer:
They can watch Beetle goes to town movie, Rainy Day Dog movie and be done by the time their mom came to get them.
Explanation:
Time she dropped them off at the theater = 1:45.
Time she said she will come back = 4:00.
Conversion:
1 Hour = 60 Minutes.
Movie Start time Length Ending Time
Beetle goes to town movie 1:55 130 minutes 1:55 + 130 = 1:55 + 2hrs 5 minutes = 4:00.
Arctic Adventure movie 2:00 125 minutes 2:00 + 125 = 2:00 + 2hrs 5 minutes = 4:05.
Rainy Day Dog movie 2:15 100 minutes 2:15 + 100 = 2:15 + 1hr 40 minutes = 3:55.
Question 5.
On each square, fill in a fraction of the square that is less than \(\frac{1}{2}\). Then use the symbols >, =, or < to compare your fraction to \(\frac{1}{2}\).
ex
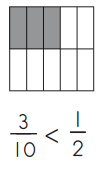
a.

Answer:
\(\frac{1}{4}\) < \(\frac{1}{2}\).
Explanation:
Fraction of the square that is less than \(\frac{1}{2}\) = 0.50.
Fraction of the square that is shaded = \(\frac{1}{4}\) = 0.25.
=> \(\frac{1}{4}\) is lesser than \(\frac{1}{2}\).
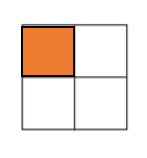
b.
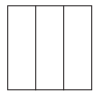
Answer:
\(\frac{1}{2}\) >\(\frac{1}{3}\).
Explanation:
Fraction of the square that is less than \(\frac{1}{2}\) = 0.5.
Fraction of the square that is shaded = \(\frac{1}{3}\) = 0.33.
=> \(\frac{1}{2}\) is greater than \(\frac{1}{3}\).

c.

Answer:
\(\frac{2}{5}\) < \(\frac{1}{2}\).
Explanation:
Fraction of the square that is less than \(\frac{1}{2}\) = 0.5.
Fraction of the square that is shaded = \(\frac{2}{5}\) = 0.4.
=> \(\frac{2}{5}\) is lesser than \(\frac{1}{2}\).
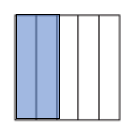
Question 6.
On each square, fill in a fraction of the square that is greater than \(\frac{1}{2}\). Then use the symbols >, =, or < to compare your fraction to \(\frac{1}{2}\).
a.
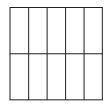
Answer:
\(\frac{6}{10}\) > \(\frac{1}{2}\).
Explanation:
Fraction of the square that is greater than \(\frac{1}{2}\) = 0.50.
Fraction of the square that is shaded = \(\frac{6}{10}\) = 0.6.
=> \(\frac{6}{10}\) is greater than \(\frac{1}{2}\).
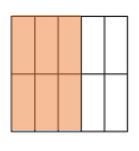
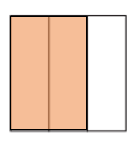
b.
Answer:
\(\frac{3}{4}\) > \(\frac{1}{2}\).
Explanation:
Fraction of the square that is greater than \(\frac{1}{2}\) = 0.50.
Fraction of the square that is shaded = \(\frac{3}{4}\) = 0.75.
=> \(\frac{3}{4}\) is greater than \(\frac{1}{2}\).

c.
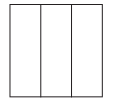
Answer:
\(\frac{1}{2}\) < \(\frac{2}{3}\).
Explanation:
Fraction of the square that is greater than \(\frac{1}{2}\) = 0.50.
Fraction of the square that is shaded = \(\frac{2}{3}\) = 0.67.
=> \(\frac{1}{2}\) is lesser than \(\frac{2}{3}\).
d.
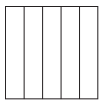
Answer:
\(\frac{1}{2}\) < \(\frac{4}{5}\).
Explanation:
Fraction of the square that is greater than \(\frac{1}{2}\) = 0.50.
Fraction of the square that is shaded = \(\frac{4}{5}\) = 0.8.
=> \(\frac{1}{2}\) is lesser than \(\frac{4}{5}\).
Question 7.
Write each of the following fractions where they belong on the number line below.
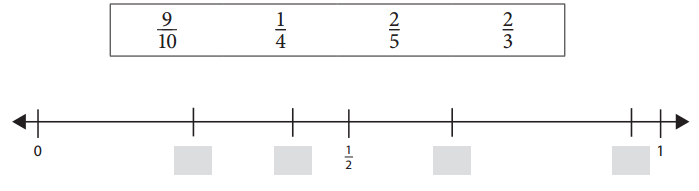
Answer:
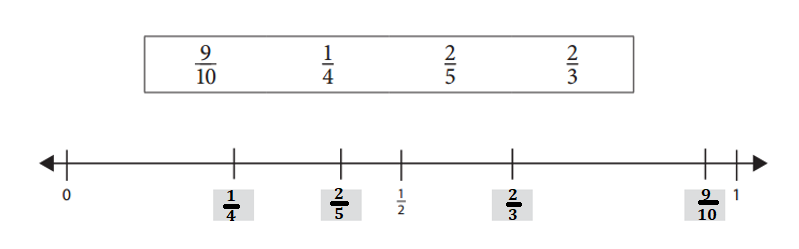
Explanation:
Given Fractions:
\(\frac{9}{10}\) = 0.9.
\(\frac{1}{4}\) = 0.25.
\(\frac{2}{5}\) = 0.40.
\(\frac{2}{3}\) = 0.67.
=> Fractions on number line:
1. \(\frac{1}{4}\)
2. \(\frac{2}{5}\)
3. \(\frac{2}{3}\)
4. \(\frac{9}{10}\)