Wondering how to find the Quotient, Remainder in Case of Division Problems? Look no further! our Worksheet on Dividend Divisor Quotient and Remainder will assist you completely. Make the most out of the Word Problems on Dividend Divisor Quotient and Remainder available and score well. Firstly try to solve the Problems in Division on your own and then cross-check the solutions with the ones available here and understand where you went wrong. Bridge the knowledge gap accordingly and enhance your problem-solving ability.
Also, Read:
Dividend Divisor Quotient Remainder Questions Worksheet
Example 1:
Divide 486 with 2 and find quotient and remainder?
Solution:
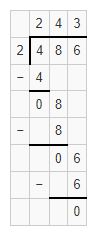
we know that 4 is exactly divisible by 2. i.e. 2 × 2=4. Place 2 as quotient and subtract 4 from 4 i.e. 4-4=0.
Bring down the digit 8. We know that 8 is exactly divisible by2 i.e. 2 × 4=8.
Place 4 as quotient and subtract 8 from 8 i.e. 8-8=0
Bring down the digit 6. We know that 6 is exactly divisible by 2. i.e. 2 ×3=6.
Place 3 as quotient and subtract 6 from 6 i.e. 6-6=0
Hence, by dividing 486 with 2 we get 243 as quotient and 0 as the remainder.
Example 2:
Find the quotient and remainder by dividing 182 by 13?
Solution:
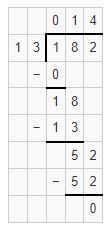
Here 1<13. Place 0 as quotient and subtract 0 from 1 i.e. 1.
Bring down the digit 8 and place it after 1. It becomes 18. We know that 18 is not exactly divisible by 13 i.e. 13 × 1=13. We will go for it.
Place 1 as quotient and subtract 13 from 18 i.e. 18-13=5
Bring down digit 2 and place it after 5. We know that 52 is exactly divisible by 13. i.e. 13 ×4=52.
Place 4 as quotient and subtract 52 from 52 i.e. 52-52=0
Hence, by dividing 182 with 13 we get 014 as quotient and 0 as the remainder.
Example 3:
Divide 34960 by 16?
Solution:
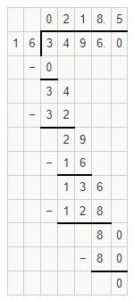
Here 3<16, Place 0 as quotient and subtract 0 from 3 i.e. 3.
Bring down the digit 4 and place it after 3. It becomes 34. We know that 34 is not exactly divisible by 16 i.e. 16 × 2=32. We will go for it.
Place 2 as quotient and subtract 32 from 34 i.e. 34-32=2
Bring down digit 9 and place it after 2. We know that 29 is not exactly divisible by 16. i.e. 16 ×1=16.
Place 1 as quotient and subtract 16 from 29 i.e. 29-16=13.
Bring down the digit 6 and place it after 13. It becomes 136.
We know that 136 is not exactly divisible by 16. i.e. 16 ×8=128. We will go for it. Place 8 as quotient and subtract 128 from 136 i.e. 136-128=8.
Bring down the digit 0 and place it after 8. It becomes 80. We know that 80 is exactly divisible by 16. i.e. 16 × 5=80. Place 5 as quotient and subtract 80 from 80 i.e. 80-80=0.
By dividing 34960 with 16 we get 2185 as quotient and 0 as the remainder.
Example 4:
Find the quotient and remainder of 2800 ÷ 22?
Solution:
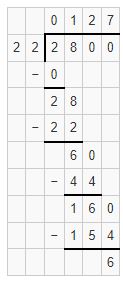
Here 2<22, Place 0 as quotient and subtract 0 from 2 i.e. 2.
Bring down the digit 8 and place it after 2. It becomes 28. We know that 28 is not exactly divisible by 22 i.e. 22 × 1=22. We will go for it.
Place 1 as quotient and subtract 22 from 28 i.e. 28-22=6
Bring down digit 0 and place it after 6. We know that 60 is not exactly divisible by 22. i.e. 22 ×2=44.
Place 2 as quotient and subtract 44 from 60 i.e. 60-44=16.
Bring down the digit 0 and place it after 16. It becomes 160.
We know that 160 is not exactly divisible by 22. i.e. 22 ×7=154. We will go for it. Place 7 as quotient and subtract 154 from 160 i.e. 160-154=6.
Hence, by dividing 2800 with 22 we get quotient as 127 and remainder as 6.
Example 5:
Find the division of 58268 ÷33?
Solution:
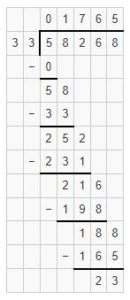
Here 5<33, Place 0 as quotient and subtract 0 from 5 i.e. 5.
Bring down the digit 8 and place it after 5. It becomes 58. We know that 58 is not exactly divisible by 33 i.e. 33 × 1=33. We will go for it.
Place 1 as quotient and subtract 33 from 58 i.e. 58-33=25
Bring down digit 2 and place it after 25. We know that 252 is not exactly divisible by 33. i.e. 33 ×7=231.
Place 7 as quotient and subtract 231 from 252 i.e. 252-231=21.
Bring down the digit 6 and place it after 21. It becomes 216.
We know that 216 is not exactly divisible by 33. i.e. 33×6=198. We will go for it. Place 6 as quotient and subtract 198 from 216 i.e. 216-198=18.
Bring down the digit 8 and place it after 18. It becomes 188. We know that 188 is not exactly divisible by 33. i.e. 33 × 5=165. Place 5 as quotient and subtract 165 from 188i.e. 188-165=23.
Hence, by dividing 58268 with 33 we get 1765 as quotient and the remainder is 23.
Example 6:
Find the division of 38482 ÷ 12?
Solution:
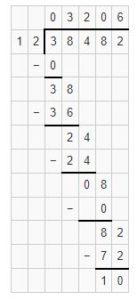
Here 12<38, Place 0 as quotient and subtract 0 from 3 i.e. 3-0=3.
Bring down the digit 8 and place it after 3. It becomes 38. We know that 38 is not exactly divisible by 12 i.e. 12 × 3=36. We will go for it.
Place 2 as quotient and subtract 36 from 38 i.e. 38-36=2
Bring down digit 4 and place it after 2. We know that 24 is exactly divisible by 12. i.e. 12 ×2=24.
Place 2 as quotient and subtract 24 from 24 i.e. 24-24=0.
Bring down the digit 8 and place it after 0. It becomes 08.
We know that 12×0=0. Place 0 as quotient and subtract 0 from 8. i.e. 8-0=8.
Bring down the digit 2 and place it after 8. It becomes 82. We know that 82 is not exactly divisible by 12. i.e. 12 × 6=72. Place 6 as quotient and subtract 72 from 82i.e. 82-72=10.
Hence, by dividing 38482 by 12 we get 3206 as quotient and 10 as the remainder. <>;
Example 7:
In a shop, there are 900 toy cars. The shopkeeper has to arrange 30 toy cars in each box. Then find out how many boxes required to arrange the toy cars?
Solution:
No.of toy cars=900
No. of toy cars arranged in each box=30
No. of boxes required to arrange 30 toy cars =900 ÷30
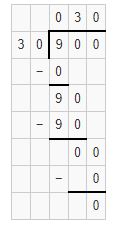
Therefore, 30 boxes required to arrange the toy cars.
Problem 8:
In a fruit shop, the shopkeeper has to parcel 70 mangoes by placing the mangoes in the boxes. Each box will contain 5 mangoes, then find out how many boxes required to arrange 70 mangoes?
Solution:
No. of mangoes have to place in boxes=70
Each box will contain mangoes=5
No. of boxes required to arrange 70 mangoes is 70÷5
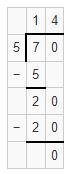
Therefore, 14 boxes required to place 70 mangoes.
Example 9:
Arjun bought a pack of 180 chocolates and visited his friends. If he gives 3 chocolates to everyone who he visited. How many friends did he visit?
Solution:
Arjun bought a pack of chocolates=180
Arjun gave no. of chocolates to everyone=3
No. of friends Arjun visited=180 ÷3
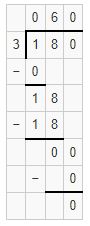
Therefore Arjun visited 60 friends.
Example 10:
Sarita has 81 chocolates. she distributes 3 chocolates to her friends in the classroom and there were no chocolates left with her. Find out how many members are there in the classroom?
Solution:
No.of chocolate Sarita has= 81
Sarita distributed chocolates to her friends=3
No.of members in the classroom are 81÷ 3
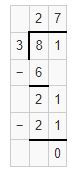
Hence, no. of members in the classroom is 27.
Example 11:
In an exhibition, there are 324 paintings to be arranged in cupboards. if 12 paintings are arranged in each cupboard. Find how many cupboards are required to arrange 324 paintings?
Solution:
No. of paintings in the exhibition=324
No. of paintings in each cupboard=12
No. of cupboards required to arrange the paintings= 324 ÷12.
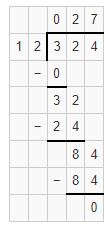
Hence, no. of cupboards required to arrange 324 paintings is 27.
Example 12:
Sita has 36 sets of earrings. She wants them to arrange in boxes so that each box will contain only two sets of earrings. Find how many boxes are required to place the earrings.
Solution:
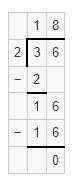
Hence, 18 boxes require to arrange the earrings.
