As a part of your Division Problems, one might encounter problems on division by 10 100 and 1000. To help you we have mentioned the procedure on how to divide by 10, 100, 1000. Check out Solved Examples on Dividing by 10, 100, 1000 and understand how the entire process works. Apply this knowledge to similar kinds of problems in your exams and score better grades in exams. Solve the Problems in Divide by 10, 100, 1000 Divisors Worksheet available and test your knowledge.
Do Refer:
- Worksheet on Division Problems by 2-Digit Divisors
- Worksheet on Dividend, Divisor, Quotient and Remainder
Example 1:
Find the quotient and remainder of 1638 ÷ 10
Solution:
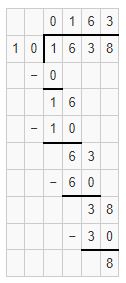
As 1 <10, place 0 as quotient and subtract 0 from 1 i.e. 1-0=1. Place 1 below line.
Bring down the digit 6 and place it after 1. It becomes 16. We know that 16 is not exactly divisible by 10. 10 × 1=10. We will go for it.
Place 1 as the quotient and subtract 10 from 16. i.e. 16-10=6. It becomes 63. We know that 63 is not exactly divisible by 10. 10 × 6=60. We will go for it.
Place 1 as the quotient and subtract 60 from 63. i.e. 63-60=3.
Bring down digit 8 and place it after 3. It becomes 38. 38 is not exactly divisible by 10. We know that 10 × 3=30.
Subtract 30 from 38. i.e. 38-30=8.
The quotient of 1638 ÷ 10 is 163 and the remainder is 8.
Example 2:
4579 ÷ 10
Solution:
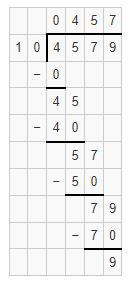
As 4 <10, place 0 as quotient and subtract 0 from 4 i.e. 4-0=4. Place 4 below the line.
Bring down the digit 5 and place it after 4. It becomes 45. We know that 45 is not exactly divisible by 10. 10 × 4=40. We will go for it.
Place 4 as the quotient and subtract 40 from 45. i.e. 45-40=5. Bring down the digit 7.It becomes 57. We know that 57 is not exactly divisible by 10. 10 × 5=50. We will go for it.
Subtract 50 from 57 i.e. 57-50=7. Bring down the digit 9 and place it after 7. It becomes 79. 79 is not exactly divisible by 10. 10 × 7=70. We will go for it.
Place 7 as the quotient and subtract 70 from 79. i.e. 79-70=9.
Therefore, on dividing 4579 ÷ 10 we get 457 as quotient and 9 as the remainder.
Tip:
By this, we can observe that when dividing with 10, units place is considered as a remainder, and remaining numbers are considered as quotient.
Example 3:
Find the quotient and remainders of the following:
I. 849 ÷ 10 Quotient=———-, Remainder=———–
II. 210 ÷ 10 Quotient=———, Remainder=.———–
III. 525 ÷10 Quotient=————, Remainder=————
Solution:
I. 84 is the quotient and 9 is the remainder.
II. 21 is the quotient and 0 is the remainder.
III.52 is the quotient and 5 is the remainder.
Example 4:
Find the division of 83600 when divided by 100?
Solution:
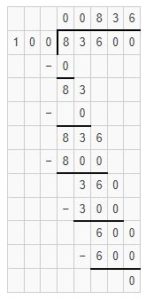
As 8<100, place 0 as quotient and subtract 0 from 8 i.e. 8-0=8.
Bring down the digit 3 and place it after 8. It becomes 83. As 83<100, place 0 as quotient and subtract 0 from 83 i.e. 83-0=83.
Bring down the digit 6 and place it after 83. It becomes 836. 836 is not exactly divisible by 100. We know that 100 × 8=800. We will go for it.
Place 8 as quotient and subtract 800 from 836 i.e. 836-800=36.
Bring down digit 0 and place it after 36. It becomes 360. 360 is not exactly divisible by 100. We know that 100 × 3=300. We will go for it.
Place 3 as quotient and subtract 300 from 360 i.e. 360-300=60.
Bring down the digit 0 and place it after 60. It becomes 600. 600 is exactly divisible by 100. We know that 100 × 6=600.
Place 6 as the quotient and subtract 600 from 600 i.e. 600-600=0.
Hence, by dividing 83600 with 100 we get 836 as quotient and 0 as the remainder.
Example 5:
Divide the 38503 by 100 and find out the quotient and remainder?
Solution:
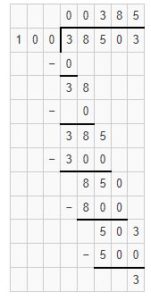
As 3<100, place 0 as quotient and subtract 0 from 3 i.e. 3-0=3. Place 3 below the line.
Bring down the digit 8 and place it after 3. It becomes 38. As 38<100, place 0 as quotient and subtract 0 from 38 i.e. 38-0=38.
Bring down the digit 5 and place it after 38. It becomes 385. 385 is not exactly divisible by 100. We know that 100 × 3=300. We will go for it.
Place 3 as quotient and subtract 300 from 385 i.e. 385-300=85.
Bring down digit 0 and place it after 85. It becomes 850. 850 is not exactly divisible by 100. We know that 100 × 8=800. We will go for it.
Place 8 as quotient and subtract 800 from 850 i.e. 850-800=50.
Bring down the digit 3 and place it after 50. It becomes 503. 503 is not exactly divisible by 100. We know that 100 × 5=500.
Place 5 as the quotient and subtract 500 from 503 i.e. 503-500=3.
Therefore, by dividing 38503 with 100 we get 385 as quotient and the remainder is 3.
Tip:
By this, we can observe that the numbers in the ones and tens place are considered as the remainders and the other digits are considered as the quotient.
Example 6:
Find the quotient and remainders of the following:
I. 1567 ÷100 Quotient=———, Remainder=————
II. 3427 ÷ 100 Quotient=———-, Remainder=———–
III. 6745 ÷100 Quotient=————, Remainder=————
Solution:
I. 15 is the quotient and 67 is the remainder.
II. 34 is the quotient and 27 is the remainder.
III.67 is the quotient and 45 is the remainder.
Example 7:
48608 ÷ 1000
Solution:
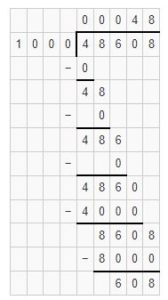
As 4<1000, place 0 in the quotient and subtract 0 from 4 i.e. 4-0=4.
Bring down the digit 8 and place it after 4. It becomes 48. As 48<1000, place 0 in the quotient and subtract 0 from 48 i.e. 48-0=48.
Bring down digit 6 and place it after 48. It becomes 486. As 486<1000, place 0 in the quotient and subtract 0 from 486 i.e. 486-0=486.
Bring down digit 0 and place it after 486. It becomes 4860. 4860 is not exactly divisible by 1000. We know that 1000 × 4=4000. We will go for it.
Place 4 in the quotient and subtract 4000 from 4860 i.e. 4860-4000=860.
Bring down the digit 8 and place it after 860. It becomes 8608. 8608 is not exactly divisible by 1000. We know that 1000 × 8=8000.
Place 8 in the quotient and subtract 8000 from 8608 i.e. 8608-8000=608.
Hence, by dividing 48608 with 1000 we get 00048 as quotient and 608 as the remainder.
Example 8:
14970 ÷ 1000
Solution:
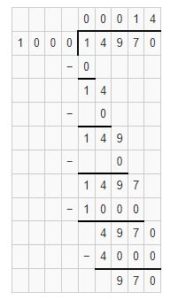
Hence, by dividing 14970 with 1000 we get 00014 as quotient and 970 as the remainder.
Tip:
The numbers in the ones and tens and hundreds are considered as the remainder and the other numbers are considered as the quotient.
Example 9:
Find the quotient and remainders of the following:
I. 16579 ÷1000 Quotient=———-, Remainder=————-
II. 28765 ÷ 1000 Quotient=———-, Remainder=————–
III. 86543 ÷ 1000 Quotient=———–, Remainder=————-
Solution:
I. 16 is considered as quotient and 579 as remainder.
II. 28 is the quotient and the remainder is 765.
III.86 is the quotient and the remainder is 543.
