Sequence means the list of items or objects placed or arranged in sequential order. Students need to identify the sequence and then find the next given object. Practicing the sequence questions will help you to increase logical thinking. But observe the objects or things carefully and then find the next object in the given sequence.
On this page, you will learn how to identify the sequence order, types of sequences, example questions on the sequence. An arithmetic sequence is a number in a particular order, the difference between two terms is constant. Sequence length is equal to the number of terms and it can be either infinite or finite.
Also, Read:
Sequence – Definition
A sequence is defined as any object or a set of numbers are arranged in a particular order followed by a rule. Each number within the sequence is named a term. If a1, a2, a3, a4,……… etc. will denote the terms of a sequence, then 1,2,3,4,…..denotes the position of the term in the sequence.
Types of Sequences
The most commonly used sequences are given below,
- Geometric Sequences
- Harmonic Sequences
- Arithmetic Sequences
- Fibonacci Numbers
Arithmetic Sequences: An arithmetic sequence is a list of numbers with a definite pattern. A sequence in which every term is adding or subtracting a definite number to the preceding number is called an arithmetic sequence. The formula for finding arithmetic sequence is,
- Sequence = x, x+2m, x+3m, x+4m,……….x+(n-1)m, where x is the first term and m is the common difference.
- The common difference, m= successive term – preceding term = x2– x1
- The general term is nth term that is x+(n-1)m
Geometric Sequences: A geometric sequence is an ordered list of numbers in which each term after the first is found by multiplying the previous one by a constant called r, the common ratio. In a sequence every object is obtained by multiplying or dividing a definite number with the preceding number is called a geometric sequence.
The formulas for finding Geometric sequence is,
- Sequence = x, xm, xm², xm³, where x is the first term and m is the common factor between the factors.
- Common factor m = successive term / preceding time.
Harmonic Sequences: A Harmonic sequence is also known as harmonic progression (HP) is defined as a sequence of real numbers which is determined by taking the reciprocals of the arithmetic sequence. Equivalently, a sequence is a harmonic sequence when each term is the harmonic mean of the neighboring terms.
- The formula to calculate the harmonic sequence or harmonic progression is,
Harmonic Mean = n /[(1/a) + (1/b)+ (1/c)+(1/d)+..]
Fibonacci Sequence: The Fibonacci sequence could be a set of numbers that starts with a one or a zero, followed by a 1, and proceeds supported on the rule that every number called a Fibonacci number is equal to the sum of the preceding two numbers.
Fibonacci Sequence is defined as, F0 = 0 and F1 = 1 and Fn = Fn-1 + Fn-2
Sequence Formulas
Some basic formula of arithmetic sequence and geometric equence are given in the below tabular form:
| Arithmetic Progression | Geometric Progression | |
| Sequence | a, a+d, a+2d, a+3d,…,a+(n-1)d | a, ar, ar2,….,ar(n-1) |
| Common Difference or Ratio | Successive term – Preceding term
Common difference = d = a2 – a1 |
Successive term/Preceding term
Common ratio = r = ar(n-1)/ar(n-2) |
| General Term is nth Term | an = a + (n-1)d | an = ar(n-1) |
| nth term from the last term | an = l – (n-1)d | an = 1/r(n-1) |
| Sum of first n terms | sn = n/2(2a + (n-1)d) | sn = a(1 – rn)/(1 – r) if r < 1
sn = a(rn -1)/(r – 1) if r > 1 |
Where, a = first term, d = common difference, r = common ratio, n = position of term, l = last term.
Example Problems on Sequence
Example 1: What is the 9th term of the sequence 2, 4, 6, 8….?
Solution:
Given, the sequence of numbers is 1, 2, 4, 6, 8,…
Now, in this sequence n is 9, and a is the first term, so a = 2
We know, the formula,
an =a1 + (n−1)d
Substitute the given values in the above formula, we get
2 + (9-1)2= 2 + (8)2 = 2+ 16 = 18
Therefore, the arithmetic sequence of the 9th term is 18.
Example 2: Find the next number in the given sequence 3, 9, 27, 81,?
Solution:
Given, the sequence numbers are 3, 9, 27, 81
Now, we can find the next sequence number.
Before that, we can identify the sequence order of a given number.
The order is , 3 x 3 = 9
9 x 2 = 27
27 x 3 = 81
So, the next sequence number is 81 x 3 = 243
Therefore, the next sequence number is 243.
Example 3: Consider the sequence 1, 3, 9, 27, 81, 243….Find the common ratio and 8th term
Solution:
Given the sequence is 1, 3, 9, 27, 81, 243,
Now, we can find the 8th term in that sequence.
First, find the preceding term,
The preceding term is multiplied by 3 to obtain the next term.
The common ratio (r) = 3/1 = 3
The nth term of the geometric sequence is denoted by the term is Tn, it is given by Tn = ar(n-1) where a is the first term and r is the common ratio.
Now, we can substitute the given value in the above formula, we get
Here a = 1, r = 3 and n = 9
So, 8th term can be calculated as T8 = 1* (3)(8-1)= 3^7 = 2187
Therefore, the 8th term in the given sequence is 2187.
Practice Questions on Sequence
Question 1:
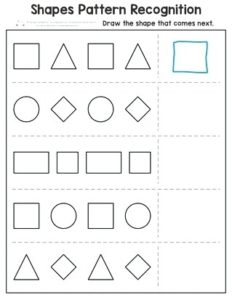
The below figure consists of various shape patterns. Students will recognize the shapes and draw the next sequence shape in the given figure boxes using a pencil.
 Question 2:
Question 2:
The below figure consists of various teddy bears with numbers and numbers in the boxes. Students will find the sequence and mark a tick on the next sequence number in the given figure.

Question 3:
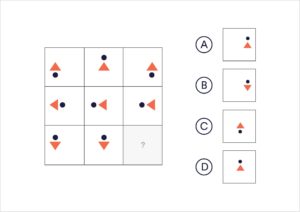
The given figure consists of various direction images but one box is blank. Students will observe the sequence and choose the correct direction image in the given options. Write it in that blank of the below figure.
 Question 4:
Question 4:
Find the next sequence numbers of the below figure. Students will write the finding number using a pencil.
 Question 5:
Question 5:
The below figure consists of different sequence numbers and some option numbers. Students will find the sequence number in place of the question mark. Write that number using a pencil.

Make your kids even more interested in Math Activities by taking help from our fun-learning Kindergarten Math Curriculum, Worksheets, Activities, Problems, Fun Games
