Do you know the meaning of the pattern? Usually, the pattern is a regular word used by everyone even small kids. For example, while purchasing anything we see the patterns on it. Similarly, in mathematics, we have the concept of pattern. It’s all about numbers and includes the different patterns. So, now we will get a sneak peek at the concept of patterns, and in what way it helps the students in math solving. Let’s see solved examples on Patterns for clear knowledge on it.
Also Check:
What is Pattern?
A pattern means a set of numbers or objects related to each other with a specific rule. It provides a common relation between the numbers. A pattern is not only a numbers pattern, it may be a word pattern, image pattern, dots pattern, etc. In maths, a pattern is a repeated system of numbers, shapes, and so on. Patterns are also known as a sequence of numbers or a series of numbers.
For example, the doors, windows of any house look in a similar pattern. In the same way, we can search for patterns in mathematics also. By knowing about the patterns students observe the relation between numbers and all number patterns are predictions.
Types of Patterns
In mathematics, we have different types to know about the concept of patterns namely arithmetic patterns, geometric patterns, shape patterns, and Fibonacci patterns, etc. In a pattern, the numbers will be in ascending order or descending order. Let’s discuss some patterns with few examples.
Arithmetic Patterns
In arithmetic patterns, the series is based on the addition and subtraction of numbers. It is also known as an algebraic pattern. If there are more than two numbers in a series by using the algebraic patterns we can find the pattern in the series given. There should be a common difference between the numbers by adding or subtracting in a series or sequence of numbers we have. The following image shows the example to understand the arithmetic pattern.
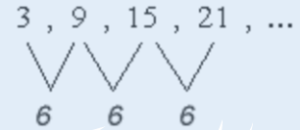
As we can see that the common difference in the above pattern is the number 6 by adding 6 to the previous number we get the next number of the pattern.
Geometric Patterns
Another type of pattern is the Geometric Pattern. It also involves a sequence of numbers depends on the multiplication and division of a sequence. Similarly, to the arithmetic pattern, if there are more than two numbers in a series we can find easily the unknown number in the geometric pattern by observing the sequence.
For example, if we have a series of numbers like 2, 4, 8, 16, __, 64, 128.
Here, if you observe the series every number is multiplied by 2 by the previous term. The third number 16 is multiplied by 2 from the previous number 8.
To find the missing number, we multiply the previous number by 2, then we get the unknown number. Thus, the unknown number is 32.
Hence, the pattern is 2, 4, 8, 16, 32, 64, 128.
Examples of Concept of Number Pattern
Example 1:
Find the missing number from the pattern 4, 8, 12, __, 20, 24, __
Solution:
Given pattern is 4, 8, 12, __, 20, 24, __
Now, we have to find the missing numbers in a sequence.
First, observe the difference between the numbers to know what type of pattern it is?
The sequence of numbers is in ascending order, and if we notice the difference is 4.
By using an arithmetic pattern, the rule to use is ‘add 4 to every previous number’.
Now, add 4 to the previous number, then easily we can find the missing numbers.
Next, add 4 to the previous number 12, then the number is 16.
Similarly, add 4 to the previous number 24, then the number is 28.
Therefore, the pattern with missing numbers is 4, 8, 12, 16, 20, 24, 28.
Example 2:
Find the next number in the series 45, 40, 35, 30, 25, __
Solution:
Given series 45, 40, 35, 30, 25, __
Here, we have to find the next number of the given series.
First, if we notice the series in decreasing order. The difference is 5.
It is in an arithmetic pattern, we have to subtract the number 5 from the previous number to get the next number.
The rule we have to use is ‘subtract 5 from the previous number’.
If we take third term 35 and subtract 5 from the previous number, then easily we got the fourth term 30.
Similarly, to find the next number subtract 5 from the previous number i.e., 25-5=20.
Hence, the next number is 20.
The complete series is 45, 40, 35, 30, 25, 20.
Example 3:
Choose the correct number in the missing place of the given series or pattern: 2, 7, 9, 3, 8, 11, 4, 9, 13, __, 10, 15.
Solution:
If you observe the series either it is in ascending order or in descending order.
Closely notice the series, in the given pattern if you add the first two numbers we get the third number.
Let’s see how the pattern is formed
Add first two numbers i.e., 2+7=9
Add four and five numbers i.e., 3+8=11
Add seven and eight numbers i.e., 4+9=13
Now, we have to find the ninth number in the series.
The next numbers are 10 and 15. The rule we followed is ‘add previous two numbers to get the third number’.
So, to get the ninth number __ + 10 = 15. Now, take 5 and add to 10 to get the 15 ie., 5 + 10 = 15.
Thus, the complete pattern is 2, 7, 9, 3, 8, 11, 4, 9, 13, 5, 10, 15.
FAQs on Concept of Pattern
1. What is a Pattern in mathematics?
A pattern is a repeated arrangement of numbers, shapes, and so on. The patterns are related to every number with a specific rule. A pattern can be not only a number it may be any object also. Simply, we can say a list of numbers that follows a certain pattern.
2. What is the rule to form a pattern?
A pattern rule is formed on basis of mathematical operations we have done on number series to know the relation between consecutive numbers. If a pattern is a numerical pattern it means a sequence of numbers, as it is created based on a rule or formula.
3. What is a repeating pattern?
You can create patterns with numbers, colors, etc. One of the types of patterns is a repeating pattern. In this pattern, the numbers just repeat over and over again is a repeating pattern.
