All the solutions provided in McGraw Hill Math Grade 5 Answer Key PDF Chapter 10 Lesson 1 Part of a Number will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 10 Lesson 1 Part of a Number
You can use bar diagrams to find parts of a number.
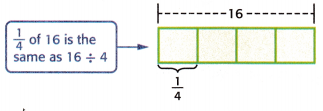
Answer:
– The first step is to draw the rectangular strip.
– Next, look at the denominator of the fraction which we want to model.
– The denominator describes how many equal parts the whole is divided into. It’s the bottom number.
– The denominator of 1/4 is 4.
– That means you should divide the rectangular strip into 4 equal parts.
– The numerator describes the number of parts you have. It’s the top number.
– The numerator of 1/4 is 1.
The above-given 1/4 of 16
Draw It
Lelah threw 16 pitches in the first inning of a softball game. Of the pitches she threw, \(\frac{3}{4}\) of them were strikes. How many strikes did she throw in the first inning?

Find \(\frac{3}{4}\) of 16.
1. The bar diagram represents the number of pitches she threw.
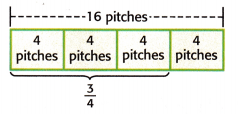
Answer:
The above-given fraction: 3/4
3/4 x 16 = 3 x 4 = 12
In fraction, 3/4; the denominator is 4 so they are divided into 4 equal parts.
The numerator is 3, so they had shown 3 equal parts. 3 x 4 = 12
Therefore, the number of pitches she threw are 12.
2. Since the denominator is 4, the bar diagram was divided into ____ equal sections.
Each section of the bar represents ____ pitches.
Answer:
The above-given fraction is 3/4
The denominator is 4 so the bar diagram is also divided into 4 equal parts. Each section represents 4 pitches.
Representation: 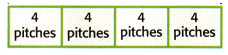
3. Use the diagram to determine \(\frac{3}{4}\) of 16.
4 + 4 + 4 = _____
\(\frac{3}{4}\)-of 16 is ____
So, Lelah threw ____ strikes.
Answer:
By using the diagram we can add the pitches
4 + 4 + 4 = 12
or we can use multiplication method
3/4 x 16 = 3 x 4 = 12
Therefore, Lelah threw 12 strikes.
Try It
Find \(\frac{1}{3}\) of 15 using a bar diagram.
1. Label the bar diagram that represents 15.
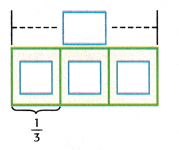
Helpful Hint
The word “of” means to multiply. So, \(\frac{1}{3}\) of 15 means \(\frac{1}{3}\) × 15.
Answer:
The above-given hint:
1/3 x 15 is equal to 5
The above boxes were divided
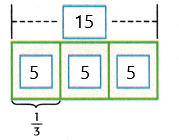
2. Since the denominator is 3, the bar diagram was divided into ____ equal sections.
Each section of the bar represents _____
Answer:
The boxes were divided into 3 sections. And each section of the bar represents 5
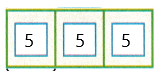
3. Use the diagram to determine \(\frac{1}{3}\) of 15.
\(\frac{1}{3}\) of 15 is the same as 15 ÷ 3, which is the same as \(\frac{1}{3}\) × 15.
What is \(\frac{1}{3}\) of 15? ____
So, \(\frac{1}{3}\) of 15 = _____
Answer:
The above-given latex sentence can be written as
1/3 of 15
= 1/3 x 15
= 5
Therefore, the answer is 5.
Talk About It
Question 1.
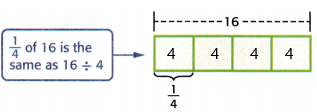
Mathematical PRACTICE 6 Explain to a Friend Explain why \(\frac{1}{4}\) of 16 is the same as 16 ÷ 4.
Answer:
To find 1/4 of 16, draw a bar diagram that represents 16. Then divide it into fourths. One of the fourths is 1/4 of 16, which is the same as 16 ÷ 4.
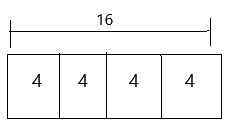
1/4 of 16 is equal to 4
16 ÷ 4 is equal to 4.
Question 2.
Explain why \(\frac{3}{4}\) of 16 is the same as 3 × 16 ÷ 4.
Answer:
If 1/4 of 16 is the same as 16 ÷ 4, then 3/4 of 16 is the same as 3 x 16 ÷ 4, since 3/4 is three times as large as 1/4.
3/4 of 16 = 3/4 x 16 = 12
3 x 16 ÷ 4
3 x 16 = 48
48 ÷ 4 = 12
both are equal.
Practice It
Draw a bar diagram to find each product.
Question 3.
12 × \(\frac{1}{2}\) = _____
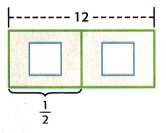
Answer:
The above-given problem is
12 x 1/2
2 x 6 = 12
we can cancel 2 and 12
Therefore, the answer is 6
The bar diagram can be represented as
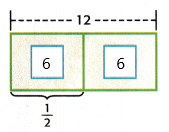
Since the denominator is 2, the bar diagram was divided into 2 equal sections.
Each section of the bar represents 6.
Question 4.
\(\frac{2}{3}\) of 15 = _____
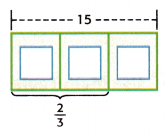
Answer:
The above-given problem is:
2/3 of 15
2/3 x 15
3 x 5 = 15 (3 and 15 gets cancel)
5 x 2 = 10
The bar diagram can be represented as;
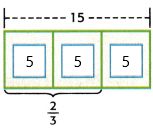
Since the denominator is 3, the bar diagram was divided into 3 equal sections.
Each section of the bar represents 5.
Question 5.
\(\frac{2}{3}\) of 8 = _____
Answer:
The above-given problem:
2/3 of 8
2/3 x 8
Express 2/3 x 18 as a single fraction.
then the fraction is 2 x 18/3
in the 3rd table, 18 get cancelled 6 times.
3 x 6 = 18
6 x 2 = 12
Therefore, 2/3 of 18 is equal to 12
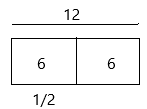
Since the denominator is 2, the bar diagram was divided into 2 equal sections.
Each section of the bar represents 6.
Question 6.
9 × \(\frac{1}{3}\) = _____
Answer:
The above-given problem:
9 x 1/3 is equal to 3
The bar diagram can be represented as:
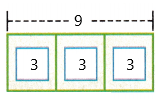
Since the denominator is 3, the bar diagram was divided into 3 equal sections.
Each section of the bar represents 3.
Question 7.
8 × \(\frac{1}{4}\) = _____
Answer:
The above-given problem;
8 x 1/4 = 2
The bar diagram can be represented as:
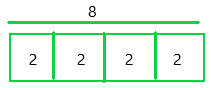
Since the denominator is 4, the bar diagram was divided into 4 equal sections.
Each section of the bar represents 2.
Question 8.
\(\frac{1}{2}\) of 16 = _____
Answer:
The above-given problem:
1/2 of 16
1/2 x 16 = 8
The bar diagram can be represented as:
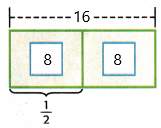
Since the denominator is 2, the bar diagram was divided into 2 equal sections.
Each section of the bar represents 8.
Question 9.
25 × \(\frac{2}{5}\) = _____
Answer:
The above-given problem;
25 x 2/5 = 5 x 2 = 10
The bar diagram can be represented as:
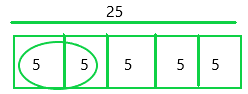
Since the denominator is 5, the bar diagram was divided into 5 equal sections.
Each section of the bar represents 5.
Question 10.
24 × \(\frac{3}{4}\) = _____
Answer:
The above-given problem
24 x 3/4 = 6 x 3 = 18
The bar diagram can be represented as:
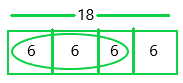
Since the denominator is 4, the bar diagram was divided into 4 equal sections.
Each section of the bar represents 6.
Apply It
Draw a bar diagram to help solve Exercises 11 and 12.
Question 11.
Leon used plant fertilizer on \(\frac{4}{7}\) of his potted flowers. If he has 28 potted flowers, on how many did he use plant fertilizer?

Answer:
The amount of fertilizer used by Leon for his potted flowers = 4/7
The estimation of potted flowers = 28
The number of plant fertilizer did he use = X
X = 4/7 x 28
X = 4 x 4
X = 16
Therefore, he used 16 plant fertilizers for 28 potted flowers.
The bar diagram can be represented as:
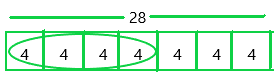
Since the denominator is 7, the bar diagram was divided into 7 equal sections.
Each section of the bar represents 4.
Question 12.
Mathematical PRACTICE 5 Use Math Tools Jeremy washed \(\frac{3}{8}\) of the plates from dinner. If 16 plates were used, how many plates did Jeremy wash?
Answer:
The number of plates he washed = 3/8
The estimation of the number of plates used = 16
The number of plates did Jeremy washed = X
X = 3/8 x 16
X = 3 x 2
X = 6
Therefore, he washed 6 plates.
The bar diagram can be represented as:
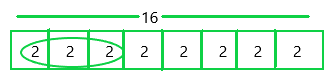
Since the denominator is 8, the bar diagram was divided into 8 equal sections.
Each section of the bar represents 2.
Question 13.
Mathematical PRACTICE 4 Model Math Write a real-world problem that could represent the bar diagram shown.
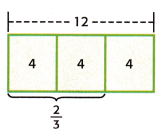
Answer:
From the bar diagram, we can write as
2/3 of 12
2/3 x 12 = 4 x 2 = 8
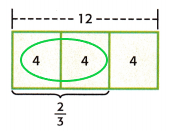
The real-world problem could be shamvitha had $12 to spend at the store. She spent 2/3 of the money he had on chocolates. How much did she spend?
Shamvitha spent $8.
Write About It
Question 14.
How can I use models to find part of a number?
Answer:
I can draw a bar diagram to model the number. I divided it into equal parts. One or more of the parts represents the part of the number.
McGraw Hill My Math Grade 5 Chapter 10 Lesson 1 My Homework Answer Key
Practice
Draw a bar diagram to find each product
Question 1.
\(\frac{2}{3}\) of 36 = ____
Answer:
The above-given problem:
2/3 of 36.
2/3 x 36 = 2 x 12 = 24
The bar diagram can be represented as:
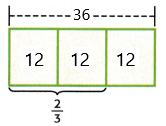
Since the denominator is 3, the bar diagram was divided into 3 equal sections.
Each section of the bar represents 12.
Question 2.
35 × \(\frac{3}{5}\) = ____
Answer:
The above-given diagram:
35 x 3/5 = 7 x 3 = 21
The bar diagram can be represented as:
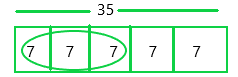
Since the denominator is 5, the bar diagram was divided into 5 equal sections.
Each section of the bar represents 7.
Problem Solving
Draw a bar diagram to help solve Exercises 3-5.
Question 3.
Hope used \(\frac{1}{3}\) of the flour in the container to make cookies. If the container holds 12 cups of flour, how many cups did Hope use?
Answer:
The amount of flour Hope used to make cookies = 1/3
The estimated cups of flour container holds = 12
The number of cups Hope uses = X
X = 1/3 x 12
X = 4
Therefore, Hope uses 4 cups of flour.
The bar diagram can be written as:
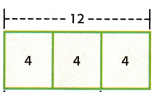
Since the denominator is 3, the bar diagram was divided into 3 equal sections.
Each section of the bar represents 4.
Question 4.
Elijah used \(\frac{3}{4}\) of the memory on his cell phone memory card. If the memory card can hold 32 gigabytes, how many gigabytes did Elijah use?
Answer:
The amount of memory Elijah used = 3/4
The estimated amount of memory = 32 gigabytes
The number of gigabytes Elijah used = X
X = 3/4 x 32
X = 3 x 8
X = 24
Therefore, Elijah used 24 gigabytes.
The bar diagram can be represented as
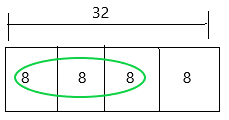
Since the denominator is 4, the bar diagram was divided into 4 equal sections.
Each section of the bar represents 8.
Question 5.
Mathematical Practice 4 Model Math Jeremy used \(\frac{5}{6}\) of a loaf of bread throughout the week. If there were 24 slices of bread, how many slices did Jeremy use?
Answer:
The amount of bread Jeremy used = 5/6
The estimated slices of bread = 24
The number of slices she used = X
X = 5/6 x 24
X = 5 x 4
X = 20
Therefore, she uses 20 slices.
The bar diagram can be represented as:
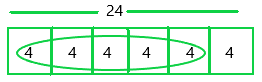
Since the denominator is 6, the bar diagram was divided into 6 equal sections.
Each section of the bar represents 4.
Question 6.
Write a real-world problem that could represent the bar diagram shown.
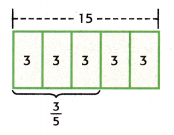
Answer:
From the above bar diagram,
3/5 x 15 = 3 x 3 = 9
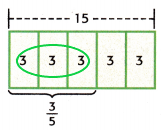
The real-world problem could be sham had $15 to spend at the store. She spent 3/5 of the money he had on drinks. How much did she spend?
Shamvitha spent $9.