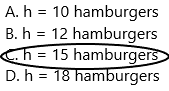All the solutions provided in McGraw Hill Math Grade 5 Answer Key PDF Chapter 10 Lesson 10 Divide Whole Numbers by Unit Fractions will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 10 Lesson 10 Divide Whole Numbers by Unit Fractions
Math in My World
Example 1
A sports Web site has score updates every \(\frac{1}{4}\) hour. How many times does the Web site have score updates in a 3-hour period?
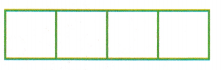
Find 3 ÷ \(\frac{1}{4}\) using models.
1. The model represents 3. How many \(\frac{1}{4}\)s are in 3?

Answer:
The above-given problem
1/4 are in 3.
This can be represented in the above diagram.
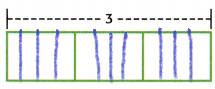
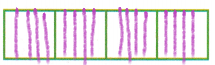
2. Divide each of the three rectangles into fourths.
Answer:
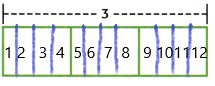
3. Count the number of fourths.
There are ___-fourths in the model.
3 ÷ \(\frac{1}{4}\) = ____
So, the Web site has ____ score updates in 3 hours.
Check You can check division problems using multiplication inverse operations.
12 × \(\frac{1}{4}\) = ![]() or ____
or ____
Answer:
Now count the rectangles
There are 12-fourths in the model.
3 ÷ 1/4
Now simplify the above equation
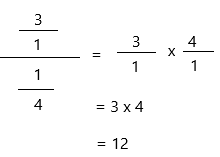
Therefore, the website has 12 score updates in 3 hours.
If we check division problems using multiplication inverse operations
then, 12 x 1/4 = 3 (or) 3/1.
Example 2
Lisa takes four apple pies to her family reunion. Each pie is cut into sixths. How many pieces of pie can Lisa serve? Find the unknown in 4 ÷ \(\frac{1}{6}\) = g.
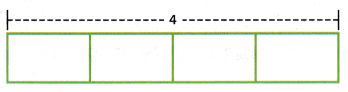
1. The model represents 4.
Answer:
The total number of apple pies = 4
First, divide the pies into six slices
The diagram can be represented as
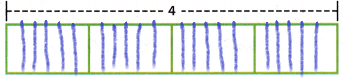
2. Divide each of the four smaller rectangles into sixths.
So, 4 ÷ \(\frac{1}{6}\) = ____
g = ____ ← unknown
Lisa can serve _____ pieces of pie.
Check Use multiplication to check your answer. ____ × \(\frac{1}{6}\) = 4
Answer:
The division of rectangles is shown above.
4 ÷ 1/6
Now calculate the division.
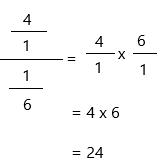
g = 24
Therefore, Lisa can serve 24 pieces of pie.
Now check by using the multiplication
24 x 1/6 = 4
Hence proved.
Talk Math
Why can you use multiplication to check your answer to a division problem?
Answer: Hence, when we multiply the quotient with the divisor and add the remainder we get the dividend back.

Guided Practice
Question 1.
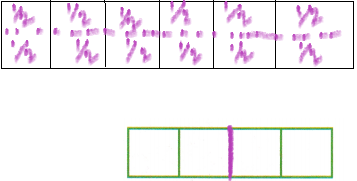
Find the quotient of 2 ÷ \(\frac{1}{3}\). Use a model. Check using multiplication.
2 ÷ \(\frac{1}{3}\) = ____
Check ____ × \(\frac{1}{3}\) = ![]() or 2
or 2
Answer:
The above-given problem:
We need to find the quotient for 2 ÷ 1/3
The diagram can be represented as:
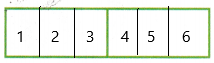
Now we have to simplify the equation.
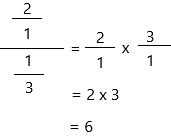
Now we have to check the answer by using the multiplication inverse.
6 x 1/3 = 2
Therefore, the answer is correct.
Independent Practice
Find each quotient. Use a model. Check using multiplication.
Question 2.
4 ÷ \(\frac{1}{3}\) = ____
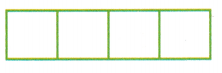
Check ____ × \(\frac{1}{3}\) =  or 4
or 4
Answer:
The above-given problem:
4 ÷ 1/3
Now we have to simplify the equation.
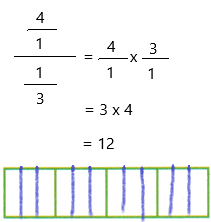
Now we have to check the answer by using multiplication.
12 x 1/3 = 4
Therefore, the answer is correct.
Question 3.
3 ÷ \(\frac{1}{5}\) = ____

Check ____ × \(\frac{1}{5}\) =  or 3
or 3
Answer:
The above-given
3 ÷ 1/5
Now simplify the equation
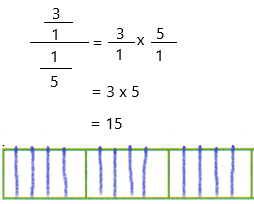
Now check the answer by using the multiplication
15 x 1/5 = 3 (or) 3/1
Therefore, the answer is correct.
Question 4.
6 ÷ \(\frac{1}{4}\) = ____

Check ____ × \(\frac{1}{4}\) =  or 6
or 6
Answer:
The above-given
6 ÷ 1/4
Now simplify the equation
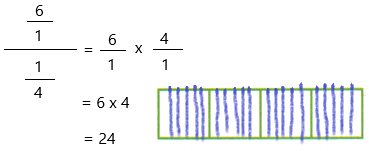
Now check the answer by using multiplication.
24 x 1/4 = 6
Hence, the answer is correct.
Question 5.
5 ÷ \(\frac{1}{4}\) = ____

Check ____ × \(\frac{1}{4}\) =  or 5
or 5
Answer:
The above-given:
5 ÷ 1/4
Now simplify the equation.
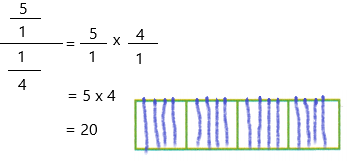
Now check the answer by using multiplication
20 x 1/4 = 20/4 = 5
Hence, the answer is correct.
Question 6.
2 ÷ \(\frac{1}{2}\) = ____

Check ____ × \(\frac{1}{2}\) =  or 2
or 2
Answer:
The above-given:
2 ÷ 1/2
Now simplify the equation.
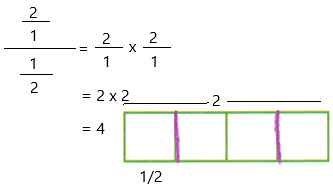
Now check the answer by using multiplication
4 x 1/2 = 4/2 = 2
Hence, the answer is correct.
Question 7.
3 ÷ \(\frac{1}{6}\) = ____

Check ____ × \(\frac{1}{6}\) =  or 3
or 3
Answer:
The above-given
3 ÷ 1/6
Now simplify the equation
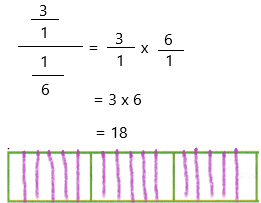
Now check the answer by using multiplication
18 x 1/6 = 18/6 = 3
Hence, the answer is correct.
Problem Solving
Mathematical PRACTICE 5 Use Math Tools Draw a model to solve each problem.
Question 8.
Denise has 4 hours to paint crafts. She would like to spend no more than \(\frac{1}{4}\) of each hour on each craft How many crafts can she paint during that time?
Answer:
The total number of hours Denise has = 4
The number of hours she would like to spend = 1/4
The number of crafts she can paint in that particular time = X
X = 4 ÷ 1/4
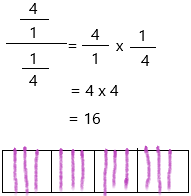
X = 16 crafts
Therefore, she could paint 16 crafts.
Question 9.
Laura has a 6-foot-long piece of ribbon that she wants to cut to make bows. Each piece needs to be \(\frac{1}{3}\)-foot long to make one bow. How many bows will she be able to make?
Answer:
The length she wants to cut the pieces = 6
The length she needs for each piece for one bow = 1/3
The number of bows she can make = X
X = 6 ÷ 1/3
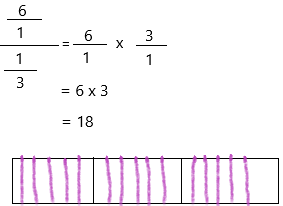
x = 18
Therefore, she can make 18 bows.
Question 10.
Ray has 8 pieces of wood to finish building a doghouse. How many pieces of wood will he have if he divides each piece in half?

Answer:
The number of wooden pieces Ray is having = 8
If wooden pieces are cut into half means 1/2 then the number of pieces he would have. Let it be X.
X = 8 ÷ 1/2
X = 8 x 2
X = 16
Therefore, she would have 16 pieces

HOT Problems
Question 11.
Mathematical PRACTICE 6 Be Precise Write and solve a real-world problem for 9 ÷ \(\frac{1}{8}\). Then explain the meaning of the quotient.
Answer:
The above-given:
9 ÷ 1/8
The problem might be sham has 9 sandwiches for his party. He will cut each sandwich into eights. How many slices of the sandwich will sham have for the party?
Let the quotient be q.
q = 9 x 8
q = 72
Therefore, the sham will have 72 slices of sandwich.
Question 12.
? Building on the Essential Question Explain the relationship between division and multiplication.
Answer:
Multiplication and division are closely related. They are basic arithmetic operations and we know that division is an inverse operation of multiplication. Multiplication means adding equal parts to form a group whereas division is the split of those equal parts from a group. So, Multiplication and Division are related to each other.
For example,
the division operation is 9 ÷ 1/8 = 72
the multiplication operation is 72 x 1/8 = 9
McGraw Hill My Math Grade 5 Chapter 10 Lesson 10 My Homework Answer Key
Practice
Find each quotient. Use a model. Check using multiplication.
Question 1.
4 ÷ \(\frac{1}{5}\) = ____
Check: _____ × \(\frac{1}{5}\) =  or 4
or 4
Answer:
The above-given:
4 ÷ 1/5
Let the quotient be q
q = 4/1 x 5/1
q = 4 x 5
q = 20
The diagram can be represented as:
Now check the answer by using multiplication
20 x 1/5 = 20/5 = 4
Hence the answer is correct.
Question 2.
6 ÷ \(\frac{1}{2}\) = ____

Check: _____ × \(\frac{1}{2}\) =  or 6
or 6
Answer:
The above-given:
6 ÷ 1/2
Let the quotient be q
q = 6/1 x 2/1
q = 6 x 2
q = 12
The multiplication operation will be:
12 x 1/2 = 6
Hence, the answer is correct.
Problem Solving
Mathematical Practice 5 Use Math Tools Draw a model to solve each problem.
Question 3.
Chef Erin has 4 pizzas that need to be cut into slices. Each slice represents \(\frac{1}{6}\) of a pizza. How many slices of pizza can she serve?
Answer:
The number of pizzas he has = 4
Each slice represents = 1/6
The number of slices of pizza he can serve = s
s = 4 ÷ 1/6
s = 4/1 x 6/1
s = 4 x 6
s = 24
Therefore, he can serve 24 slices of pizza.
The model can be represented as:

Question 4.
A baker cuts 3 cakes into pieces. Each piece represents \(\frac{1}{8}\) of a cake. What is the total number of pieces?
Answer:
The number of cakes = 3
The piece each represents = 1/8
The total number of pieces = X
X = 3 ÷ 1/8
X = 3/1 x 8/1
X = 3 x 8
X = 24
Therefore, the total number of pieces is 24.
The model can be represented as;

Question 5.
Mathematical PRACTICE 7 Identify Structure Circle the model below that represents 2 ÷ \(\frac{1}{3}\).
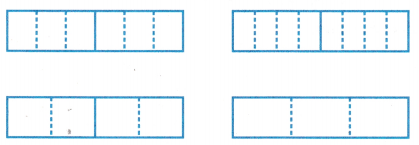
Answer:
The above-given:
2 ÷ 1/3
If we simplify this we get:
= 2/1 x 3/2
= 2 x 3
= 6
So we divide the box into 2 sections.
In each section we have to divide into 3 parts.
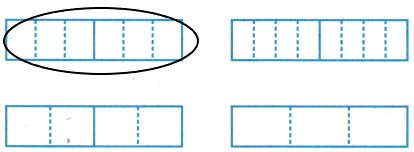
Test Practice
Question 6.
Karen uses five pounds of hamburger to grill hamburgers. Each pound is divided into thirds to make each hamburger. How many hamburgers can Karen serve? Find the unknown in 5 ÷ \(\frac{1}{3}\) = h.

A. h = 10 hamburgers
B. h = 12 hamburgers
C. h = 15 hamburgers
D. h = 18 hamburgers
Answer: Option C is correct.
The above-given:
5 ÷ 1/3 = h
now simplify the equation
5/1 x 3/1 = h
5 x 3 = h
15 = h
Therefore, he can serve 15 hamburgers.