All the solutions provided in McGraw Hill My Math Grade 5 Answer Key PDF Chapter 10 Check My Progress will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Chapter 10 Check My Progress Answer Key
Check My Progress Page No. 731-732
Vocabulary Check
Draw lines to match each word with its correct description or meaning.

Answer:

Concept Check
Estimate each product. Draw a bar diagram if necessary.
Question 4.
\(\frac{1}{5}\) × 11
_________
Answer:
The above-given latex sentence can be written as 1/5
1/5 x 11 that is nothing but 11/5
A simple way to visualize, or see, fractions are using fraction bar models.
A fraction bar model is a drawing of a fraction using rectangles.
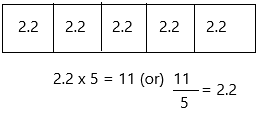
Question 5.
\(\frac{3}{5}\) × \(\frac{10}{11}\)
_________
Answer:
The above-given latex sentence can be written as 3/5 and 10/11
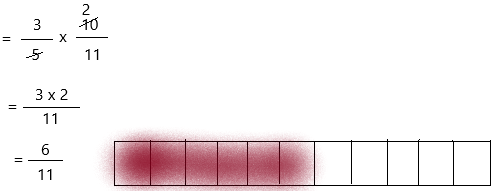
– The first step is to draw the rectangular strip.
– Next, look at the denominator of the fraction which we want to model.
– The denominator describes how many equal parts the whole is divided into. It’s the bottom number.
– The denominator of 6/11 is 11.
– That means you should divide the rectangular strip into 11 equal parts.
– The numerator describes the number of parts you have. It’s the top number.
– The numerator of 6/11 is 6.
– That means you should colour or shade 6 out of the 11 parts of the rectangular strip.
Question 6.
4\(\frac{7}{8}\) × 2\(\frac{1}{12}\)
_________
Answer:
The above-given latex sentence can be written as 4 7/8 and 2 1/12
We need to convert them into proper fractions.
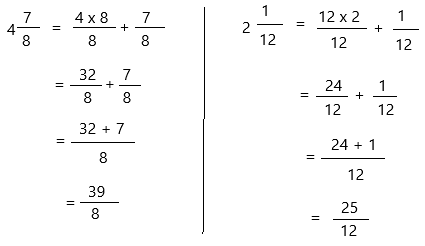
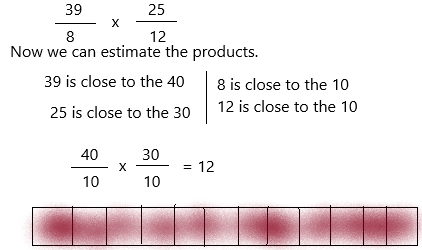
Here are some fraction bar models for halves, thirds, fourths, sixths, and eighths.
We got the bar model as one whole.
Question 7.
Shade the model to find the product. Write in the simplest form. 3
2 × \(\frac{3}{5}\) = _____
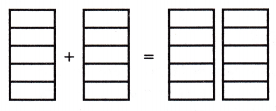
Answer:
The above-given latex sentence is 2 x 3/5
Multiply all of the numerators by each other. Do the same with the denominators and form a new fraction with these values:
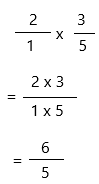
Then the product is 6/5
Multiply. Write in simplest form.
Question 8.
\(\frac{2}{5}\) × 16 = _____
Answer:
\(\frac{2}{5}\) can be written as 2/5
Multiply all of the numerators by each other. Do the same with the denominators and form a new fraction with these values:
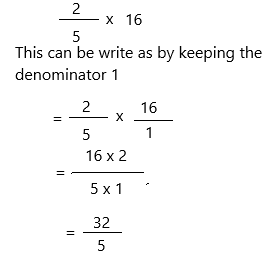
Question 9.
18 × \(\frac{1}{6}\) = _____
Answer:
\(\frac{1}{6}\) can be written as 1/6
Multiply all of the numerators by each other. Do the same with the denominators and form a new fraction with these values:
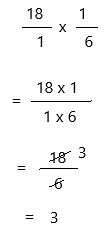
Question 10.
6 × \(\frac{3}{5}\) = _____
Answer:
\(\frac{3}{5}\) can be written as 3/5
Multiply all of the numerators by each other. Do the same with the denominators and form a new fraction with these values:
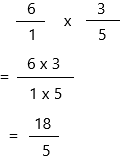
Problem Solving
Question 11.
Diane sent 25 invitations to her birthday party. If \(\frac{1}{6}\) of the invitations were for her family, about how many invitations were for her family?
Answer:
The number of invitations Diane sent to her birthday party was 25
The number of invitations to her family = 1/6
The number of invitations she sent to her family. Let it be x.
x = 1/6 x 25

Therefore, Diane sent 4 invitations to her family.
Question 12.
A recipe calls for \(\frac{2}{3}\) cup of brown sugar. Marilyn is making 5 batches. How many cups of brown sugar should Marilyn use?
Answer:
The recipe calls for the amount of brown sugar = 2/3 cups
The number of batches Marilyn is making = 5
The number of cups of brown sugar should Marilyn use = x
x = 2/3 x 5
x = 2 x 5/3
x = 10/3
x = 3.33
Therefore, Marilyn uses 3.33 cups of brown sugar to make 5 batches.
Question 13.
There are 24 students in Mr. Sampson’s math class. One-third of the students received an A on a recent test. How many students received an A on the test?
Answer:
The total number of students in maths class = 24
The amount of students received an A on a test = 1/3
The number of students received an A on the test = x
x = 24 x 1/3
x = 24 x 1/3
x = 24/3
x = 8
Therefore, 8 students received an A on the test.
Question 14.
Jacinta is working on a jigsaw puzzle that has 403 pieces. She has completed \(\frac{1}{4}\) of the puzzle. About how many pieces has she placed in the puzzle?

Answer:
The total number of pieces in a jigsaw puzzle Jacinta is working = 403
The number of pieces she has completed = 1/4
The number of pieces she has placed in the puzzle = x
x = 403 x 1/4
x = 403/4
x = 100.75
Therefore, she placed 100.75 pieces in the jigsaw puzzle.
Test Practice
Question 15.
George has a collection of 16 postcards from the states shown in the table. How many postcards does he have from California?
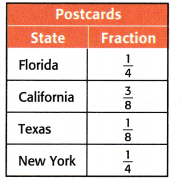
A. 12 postcards
B. 10 postcards
C. 8 postcards
D. 6 postcards
Answer: Option D is correct.
The total number of postcards = 16
The postcards he has in fractions for California = 3/8
The number of postcards = x
x = 16 x 3/8
x = 2 x 3
x = 6
Therefore, he has 6 postcards for california.
Check My Progress Page No. 757-758
Vocabulary Check
Question 1.
Fill in the blank with the correct term or number to complete the sentence.
Scaling is the process of ____ a number when you multiply by a fraction that is greater than or less than 1.
Answer: resizing
Scaling is the factor which is used to represent the object size. The size of the object can be shown by increasing or decreasing its original size. In general, the represented size of the object increased for the small object whereas it decreased for the bigger object. Scaling is used for better viewing of an object.
Concept Check
Shade the models to find each product. Write in simplest form.
Question 2.
\(\frac{2}{5}\) × \(\frac{1}{2}\) = _____
Answer:
\(\frac{2}{5}\) can be written as 2/5
\(\frac{1}{2}\) can be written as 1/2
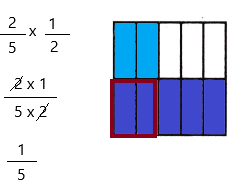
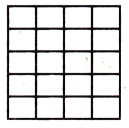
Question 3.
\(\frac{3}{4}\) × \(\frac{3}{5}\) = _____
Answer:
\(\frac{3}{4}\) can be written as 3/4
\(\frac{3}{5}\) can be written as 3/5
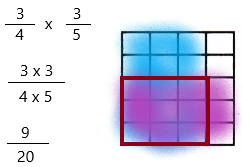
– The denominator describes how many equal parts the whole is divided into. It’s the bottom number.
– The denominator of 9/20 is 20.
– That means you should divide the rectangular strip into 20 equal parts.
– The numerator describes the number of parts you have. It’s the top number.
– The numerator of 9/20 is 9.
– That means you should mark or shade 9 out of the 20 parts of the rectangular box.
Multiply. Write in simplest form.
Question 4.
\(\frac{1}{2}\) × \(\frac{4}{9}\) = _____
Answer:
\(\frac{1}{2}\) can be written as 1/2
\(\frac{4}{9}\) can be written as 4/9
Multiply all of the numerators by each other. Do the same with the denominators and form a new fraction with these values:
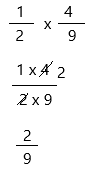
Question 5.
\(\frac{4}{5}\) × \(\frac{5}{6}\) = _____
Answer:
\(\frac{4}{5}\) can be written as 4/5
\(\frac{5}{6}\) can be written as 5/6
Multiply all of the numerators by each other. Do the same with the denominators and form a new fraction with these values:
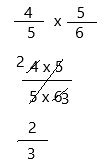
Question 6.
\(\frac{1}{5}\) × 4\(\frac{2}{3}\) = _____
Answer:
\(\frac{1}{5}\) can be written as 1/5
4\(\frac{2}{3}\) can be written as 4 2/3
4 2/3 is a mixed fraction. So we need to convert it into a proper fraction.
4 2/3 = 3 x 4/3 + 2/3 = 12/3 + 2/3 = 14/3.
Multiply all of the numerators by each other. Do the same with the denominators and form a new fraction with these values:
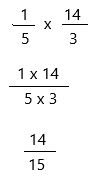
Question 7.
7\(\frac{1}{8}\) × 2\(\frac{5}{6}\) = _____
Answer:
7\(\frac{1}{8}\) can be written as 7 1/8
7 1/8 is a mixed fraction. So we have to convert it into a proper fraction.
7 1/8 = 8 x 7/8 + 1/8 = 56/8 + 1/8 = 57/8
2\(\frac{5}{6}\) can be written as 2 5/6
2 5/6 is a mixed fraction. So we have to convert it into a proper fraction.
2 5/6 = 6 x 2/6 + 5/6 = 12/6 + 5/6 = 17/6
Multiply all of the numerators by each other. Do the same with the denominators and form a new fraction with these values:

Without multiplying, circle whether each product is greater than, less than, or equal to the whole number.
Question 8.
4\(\frac{1}{8}\) × 7
greater than
less than
equal to
Answer:
The above-given latex sentence can be written as 4 1/8
4 1/8 x 7
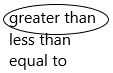
Question 9.
\(\frac{3}{5}\) × 1
greater than
less than
equal to
Answer:
The above-given latex sentence can be written as 3/5
3/5 x 1
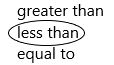
Problem Solving
Question 10.
Tom spent \(\frac{1}{6}\) of the day working in the flower bed. Tom spent \(\frac{2}{3}\) of that time adding mulch to the flower bed. What fraction of the day did Tom spend adding mulch?
Answer:
Tom spent the amount of day working in the flower bed = 1/6
The tom spent the amount of time adding mulch to the flower bed = 2/3
The amount of day Tom spends adding mulch = X
X = 1/6 x 2/3
X = 1 x 2/6 x 3
X = 2/18
X = 1/9
Therefore, Tom spends 1/9th of the day adding mulch to the flower bed.
Question 11.
Nick spent 1\(\frac{3}{4}\) hours doing homework. Of that time, \(\frac{2}{3}\) was spent on a social studies project. How many hours did Nick spend working on the project?
Answer:
The number of hours Nick spent on doing homework = 1 3/4 = 7/4
The number of hours Nick spent on social studies = 2/3
The number of hours did Nick spend working on the project = x
x = 7/4 x 2/3
x = 7 x 2/4 x 3
x = 14/12
x = 7/6
Therefore, 7/6 hours he spends on the project.
Question 12.
Anita grew a garden with \(\frac{3}{4}\) of the area for vegetables. In the vegetable section, \(\frac{1}{6}\) of the area is carrots. What fraction of the total garden is carrots?
Answer:
The area for vegetables = 3/4
The area for carrots = 1/6
The total garden is carrots = x
x = 3/4 x 1/6
x = 3 x 1/4 x 6
x = 3/24
x = 1/8
Therefore, the total garden is carrots are 1/8.
Test Practice
Question 13.
Mr. Taylor collected apples on Friday. On Saturday, he collected \(\frac{2}{3}\) of the amount collected on Friday. How many bushels of apples did Mr Taylor collect on Saturday?
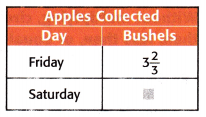
A. 1\(\frac{2}{3}\) bushels
B. 1\(\frac{4}{9}\) bushels
C. 2\(\frac{2}{3}\) bushels
D. 2\(\frac{4}{9}\) bushels
Answer: Option D is correct.
The number of apples he collected on Friday = 2/3
The bushels of apples collected on Friday = 3 2/3 = 11/3
We need to find out the bushels of apples collected on Saturday. Let it be x.
x = 2/3 x 11/3
Multiply all of the numerators by each other. Do the same with the denominators and form a new fraction with these values:
x = 11 x 2/3 x 3
x = 22/9
22 ÷ 9 = 2R4, therefore:
x = 2 4/9.