All the solutions provided in McGraw Hill My Math Grade 5 Answer Key PDF Chapter 10 Multiply and Divide Fractions will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 10 Multiply and Divide Fractions
Essential Question?
What strategies can be used to multiply and divide fractions?
Answer:
– To multiply fractions, all you have to do is multiply the numerators and denominators and simplify the result.
– To divide the fractions, you simply have to reciprocal the numerator and denominator of one of the fractions, multiply the result by the other fraction and simplify.
Am I Ready?
Estimate. Use rounding. Show how you estimated.
Question 1.
8\(\frac{5}{6}\) + 7\(\frac{1}{5}\) ≈ ____
Answer:
– First, convert mixed numbers to improper fraction
8 5/6 = 6 x 8/6 + 5/6 = 48/6 + 5/6 = 53/6
7 1/5 = 5 x 7/5 + 1/5 = 35/5 + 1/5 = 36/5
– Now find the common denominator
53/6 + 36/5

In decimals, we can write as 16.033
we can round it as 16.
Question 2.
17\(\frac{1}{4}\) – 3\(\frac{7}{8}\) ≈ ____
Answer:
– First, convert mixed numbers to improper fraction
17 1/4 = 17 x 4/4 + 1/4 = 68 + 1/4 = 69/4
3 7/8 = 3 x 8/8 + 7/8 = 24 + 7/8 = 31/8
– Now we have to find the common denominator

In decimal, we can write it as 13.375
we can round it as 13.
Question 3.
Tyra filled the two water coolers shown with flavoured sports drinks. About how many gallons of sports drink does she have altogether?

Answer:
The above-given gallons:
4 7/8 and 5 1/4
We need to find out the number of gallons of sports drink she has altogether
add both gallons.
4 7/8 + 5 1/4
– First, convert mixed numbers to improper fraction
4 7/8 = 4 x 8/8 + 7/8 = 32 + 7/8 = 39/8
5 1/4 = 5 x 4/4 + 1/4 = 20 + 1/4 = 21/4
– Now we have to find out the common denominator.

In decimals, we can write as 10.125
Therefore, she has altogether is 10.125 gallons.
Estimate. Use rounding or compatible numbers. Show how you estimated.
Question 4.
196 × 12 ≈ ____
Answer:
– Multiplication is the process of calculating the product of two or more numbers. The multiplication of numbers say, ‘a’ and ‘b’, is stated as ‘a’ multiplied by ‘b’. (or)
– the multiplication of two numbers represents the repeated addition of one number with respect to another. These numbers can be whole numbers, natural numbers, integers, fractions, etc. If m is multiplied by n, then it means either m is added to itself ‘n’ a number of times or vice versa.
Multiplication formula:
The multiplication formula is given by:
Multiplier × Multiplicand = Product
– The multiplicand is the total number of objects in each group
– The multiplier is the number of equal groups
– Product is the result of multiplication of multiplier and multiplicand
– When multiplying different digit numbers, the given numbers are placed and aligned one below the other in the correct column of their place value and then they are multiplied as shown below :
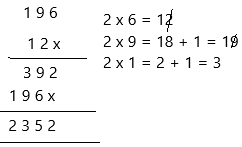
– Now we multiply the numbers using the rounding method.
196 is close to 200
12 is close to the 10
Now multiply 200 by 10
200 x 10 = 2000
It is close to the actual product, hence we can say that the answer is reasonable.
Question 5.
79 × 31 ≈ ____
Answer:
– Multiplication is the process of calculating the product of two or more numbers. The multiplication of numbers say, ‘a’ and ‘b’, is stated as ‘a’ multiplied by ‘b’. (or)
– the multiplication of two numbers represents the repeated addition of one number with respect to another. These numbers can be whole numbers, natural numbers, integers, fractions, etc. If m is multiplied by n, then it means either m is added to itself ‘n’ a number of times or vice versa.
Multiplication formula:
The multiplication formula is given by:
Multiplier × Multiplicand = Product
– The multiplicand is the total number of objects in each group
– The multiplier is the number of equal groups
– Product is the result of multiplication of multiplier and multiplicand
using rounding method:
79 is close to the 80
31 is close to the 30
Now multiply 80 by 30
Now, the estimated product is:
80 x 30 = 2400
The actual product is 79 x 31 = 2449
Therefore, it is close to the actual product, hence e can say that the answer is reasonable.
Question 6.
304 ÷ 6 ≈ ____
Answer:
The division is the process of sharing a collection of items into equal parts and is one of the basic arithmetic operations.
The division of any expression follows the division algorithm given below.
Dividend = Divisor × Quotient + Remainder
Division Rule:
Division rule involves four steps; they are:
Step 1: Identify the dividend and divisor and then write in the respective places.
Step 2: Multiply the divisor with a suitable number such that we get a result close to the dividend.
Step 3: Subtract the values in the dividend column.
Step 4: Now, bring down the result and repeat the preceding two steps until the remainder is less than the divisor.
Now we can use the rounding method
304 is close to 300
Now divide 300 by 6.

The estimated quotient is close to the actual quotient.
Hence the answer is reasonable.
Question 7.
558 ÷ 8 ≈ ____
Answer:
The division is the process of sharing a collection of items into equal parts and is one of the basic arithmetic operations.
The division of any expression follows the division algorithm given below.
Dividend = Divisor × Quotient + Remainder
Division Rule:
Division rule involves four steps; they are:
Step 1: Identify the dividend and divisor and then write in the respective places.
Step 2: Multiply the divisor with a suitable number such that we get a result close to the dividend.
Step 3: Subtract the values in the dividend column.
Step 4: Now, bring down the result and repeat the preceding two steps until the remainder is less than the divisor.
Now we can use the rounding method
558 is close to the 560
now divide 560 by 8

The estimated quotient is 70
The actual quotient is 69.75
Therefore, the estimated quotient is very close to the actual product. Hence, the answer is reasonable.
Add or subtract. Write in the simplest form.
Question 8.
\(\frac{1}{6}\) + \(\frac{1}{6}\) = ____
Answer:
1/6 + 1/6
Now add both the fractions.
= 1 + 1/6
= 2/6
= 1/3
In decimals, we can write them as 0.333
Question 9.
\(\frac{3}{4}\) + \(\frac{2}{5}\) = ____
Answer:
The above-given is:
3/4 + 2/5

Question 10.
\(\frac{8}{9}\) – \(\frac{5}{9}\) = ____
Answer:
The above-given is 8/9 and 5/9
Here, both fractions are having a common denominator.
= 8 – 5/9
= 3/9
= 1/3
Question 11.
\(\frac{7}{12}\) – \(\frac{1}{12}\) = ____
Answer:
The above-given fractions are 7/12 and 1/12
Here, both fractions are having a common denominator.
= 7 – 1/12
= 6/12
= 1/2
My Math Words
Review Vocabulary
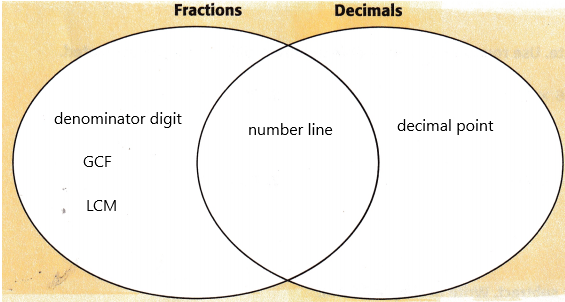
decimal point denominator digit
divide equivalent greatest common factor (GCF)
least common multiple (LCM) mixed numbers multiply
number line
Making Coñnections
Use the Venn diagram to categorize the review vocabulary.
Answer:
How is adding and subtracting fractions similar to adding and subtracting whole numbers?
Answer:
As a review, similar fractions (also like fractions) are fractions having the same denominators.
The following are the steps on how to add similar fractions:
Step 1: Ensure that all denominators are the same.
Step 2: Add all the numerators. The sum will be the numerator of our answer.
Step 3: Copy the denominator. This will be the denominator of our answer.
Step 4. Add all the whole numbers if it is mixed numbers.
Step 5. Convert your answer into its lowest term or mixed numbers.
– Dealing with the addition of similar fractions is quite simple. You just have to ensure that the denominators are the same so that you can proceed to add the numerators.
– Subtracting similar fractions has the same procedure as adding similar fractions. The only difference is that you will be dealing with subtraction.
My Vocabulary Cards
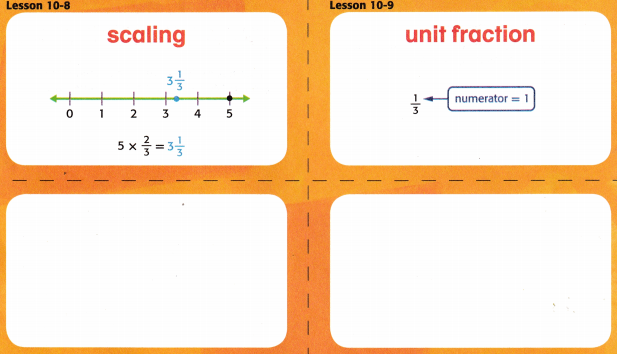
Ideas for Use
- During the year, create a separate stack of cards for key math verbs, such as scaling. They will help you in problem-solving.
- Use the blank cards to write review vocabulary cards.
- Group-like ideas you find throughout the chapter, such as the relationship between multiplication and division. Use the blank cards to write notes about these concepts.
A fraction with a numerator of 1
The Latin root fract means ‘break. How does this relate to the meaning of fractions?
Answer:
Fractions with numerator 1 are called unit fractions. Proper fractions. Fractions in which the numerator is less than the denominator are called proper fractions.
For example, fractions are defined as the parts of a whole. The whole can be an object or a group of objects. In real life, when we cut a piece of cake from the whole of it, then the portion is the fraction of the cake. A fraction is a word that is originated from Latin. In Latin, “Fractus” means “broken”. In ancient times, the fraction was represented using words. Later, it was introduced in numerical form.
– Generally, the fraction can be a portion of any quantity out of the whole thing and the whole can be any specific things or value.
– coming to the unit fractions, a fraction is known as a unit fraction when the numerator is equal to 1.
One half of whole = 1/2
One-third of whole = 1/3
One-fourth of whole = 1/4
One-fifth of whole = 1/5
The process of resizing a number when it is multiplied by a fraction that is greater than or less than 1.
The scale has multiple meanings. What might scale mean in a measurement problem?
Answer:
There are three conditions which give the different result when whole number is multiplied by fraction.
First case: If we multiply the whole number with a fraction greater than 1 then it will resultant value will become greater. Example: 5 Is a whole number and if multiplied it by fraction greater than 1.
second case: If we multiply the whole number with a fraction less than 1 then it will resultant value will become lesser. Example: 5 Is a whole number and if we multiplied it by fraction lesser than 1.
Third case: If we multiply the whole number with a fraction equal to 1 then it will resultant value will be same as there will be no change. Example: 5 Is a whole number and if we multiplied it by fraction equal to 1.


My Foldable
Foldables Follow the steps on the back to make your Foldable.
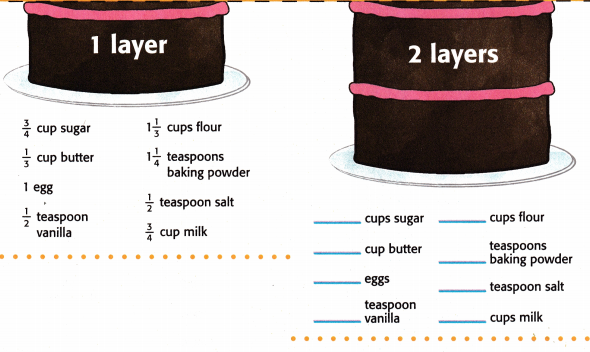
Answer:
Here, for 1 layer all the measurements are given.
And for 2 layers of cake we need to write the quantities.
for 1 layer of cake, 3/4th cup of sugar is used.
for 2 layers of cake, 3/4 + 3/4 = 6/4 = 3/2 cups of sugar is used.
for 1 layer of cake, 1/3 cup of butter is used.
for 2 layers of cake, 1/3 + 1/3 = 2/3 cups of butter is used.
for 1 layer of cake, 1 egg is used.
for 2 layers of cake, 1 + 1 = 2 eggs are used.
for 1 layer of cake, 1/2 teaspoon vanilla flavour is used
for 2 layers of cake, 1/2 + 1/2 = 2/2 = 1 teaspoon vanilla flavour is used.
for 1 layer of cake, 1 1/3 cups flour nothing but 3 x 1/3 + 1/3 = 3 + 1/3 = 4/3
for 2 layers of cake, 4/3 + 4/3 = 8/3 cups flour is used.
for 1 layer of cake, 1 1/4 teaspoons of baking powder are used. (5/4)
for 2 layers of cake, 5/4 + 5/4 = 10/4 = 5/2 teaspoons of baking powder is used.
for 1 layer of cake, 1/2 teaspoon of salt is used.
for 2 layers of cake, 1/2 + 1/2 = 2/2 = 1 teaspoon salt is used.
for 1 layer of cake, 3/4 th cup of milk is used.
for 2 layers of milk, 3/4 + 3/4 = 6/4 = 3/2 cups of milk are used.

Foldables
study organizer

___ cups sugar
____ cups butter
____ eggs
____ teaspoons vanilla
____ cups flour
____ teaspoons baking powder
____ teaspoons salt
____ cups milk
Answer:
Now we have to write the quantities for 4 layers of cake.
By taking the above quantities, we can write the measurements.
for 1 layer of cake, 3/4th cup of sugar is used.
for 4 layers of cake, 3/4 + 3/4 + 3/4 + 3/4 = 12/4 = 3. Therefore, 3 cups of sugar are needed.
for 1 layer of cake, 1/3 cup of butter is used.
for 4 layers of cake, 1/3 + 1/3 + 1/3 + 1/3 = 4/3 cups of butter is used.
for 1 layer of cake, 1 egg is used.
for 4 layers of cake, 4 eggs are used.
for 1 layer of cake, 1/2 teaspoon vanilla flavour is used
for 4 layers of cake, 1/2 + 1/2 + 1/2 + 1/2= 4/2 = 2 teaspoon vanilla flavour is used.
for 1 layer of cake, 1 1/3 cups flour nothing but 3 x 1/3 + 1/3 = 3 + 1/3 = 4/3
for 4 layers of cake, 4/3 + 4/3 + 4/3 + 4/3 = 16/3 cups flour is used.
for 1 layer of cake, 1 1/4 teaspoons of baking powder are used. (5/4)
for 4 layers of cake, 5/4 + 5/4 + 5/4 + 5/4= 20/4 = 5 teaspoons of baking powder is used.
for 1 layer of cake, 1/2 teaspoon of salt is used.
for 4 layers of cake, 1/2 + 1/2 + 1/2 + 1/2 = 4/2 = 2 teaspoon salt is used.
for 1 layer of cake, 3/4 th cup of milk is used.
for 4 layers of milk, 3/4 + 3/4 + 3/4 + 3/4 = 12/4 = 3 cups of milk are used.

___ cups sugar
____ cups butter
____ eggs
____ teaspoons vanilla
____ cups flour
____ teaspoons baking powder
____ teaspoons salt
____ cups milk
Answer:
for 1 layer of cake, 3/4th cup of sugar is used.
for 3 layers of cake, 3/4 + 3/4 + 3/4 = 9/4. Therefore, 9/4 cups of sugar are needed.
for 1 layer of cake, 1/3 cup of butter is used.
for 3 layers of cake, 1/3 + 1/3 + 1/3 = 3/3 = 1. Therefore, 1 cup of butter is used.
for 1 layer of cake, 1 egg is used.
for 3 layers of cake, 1 + 1 + 1 = 3 eggs are used.
for 1 layer of cake, 1/2 teaspoon vanilla flavour is used
for 3 layers of cake, 1/2 + 1/2 + 1/2 = 3/2 teaspoon vanilla flavour is used.
for 1 layer of cake, 1 1/3 cups flour nothing but 3 x 1/3 + 1/3 = 3 + 1/3 = 4/3
for 3 layers of cake, 4/3 + 4/3 + 4/3 = 12/3 = 4 cups flour is used.
for 1 layer of cake, 1 1/4 teaspoons of baking powder are used. (5/4)
for 3 layers of cake, 5/4 + 5/4 + 5/4= 15/4 teaspoons of baking powder is used.
for 1 layer of cake, 1/2 teaspoon of salt is used.
for 3 layers of cake, 1/2 + 1/2 + 1/3 = 3/2 teaspoon salt is used.
for 1 layer of cake, 3/4 th cup of milk is used.
for 3 layers of milk, 3/4 + 3/4 + 3/4 = 9/4 cups of milk are used.