All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 9 Lesson 9 Multiply Fractions by Whole Numbers will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 4 Answer Key Chapter 9 Lesson 9 Multiply Fractions by Whole Numbers
You can use models and equations to multiply a fraction by a whole number.
Math in My World
Example 1
Each card on a trivia game has 6 questions. Each question represents \(\frac{1}{6}\) of the questions on the card. Caleb correctly answered 4 of the questions. What fraction of the questions on a card did he answer correctly?

Find 4 × \(\frac{1}{6}\).
One Way:
Use repeated addition.
Use repeated addition to write an equation.
4 × \(\frac{1}{6}\) = \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\)
= \(\frac{4}{6}\) Add like fractions.
= ![]() Simplify.
Simplify.
Another Way:
Use models.
The number line shows the first four multiples of \(\frac{1}{6}\).
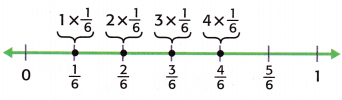
So, 4 × \(\frac{1}{6}\) = ![]() .
.
Check: Use fraction tiles. 4 × \(\frac{1}{6}\) = \(\frac{4}{6}\) or ![]() .
.

Answer:
Fraction of the questions on a card he answer correctly = \(\frac{4}{6}\) or \(\frac{2}{3}\)
Explanation:
Number of questions on each card on a trivia game has = 6.
Number of each question on the card represents = \(\frac{1}{6}\)
Number of questions Caleb correctly answered = 4.
Fraction of the questions on a card he answer correctly = Number of questions Caleb correctly answered × Number of each question on the card represents
= 4 × \(\frac{1}{6}\)
= \(\frac{4}{6}\) ÷ \(\frac{2}{2}\)
= \(\frac{2}{3}\)
1. Use repeated addition:
4 × \(\frac{1}{6}\) = \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\)
= \(\frac{4}{6}\)
2. Use models.
The number line shows the first four multiples of \(\frac{1}{6}\).

So, 4 × \(\frac{1}{6}\) = \(\frac{4}{6}\)
3. Use fraction tiles.

4 × \(\frac{1}{6}\) = \(\frac{4}{6}\) ÷ \(\frac{2}{2}\) = \(\frac{2}{3}\)
You can use equations and properties to multiply a fraction by a whole number.
Example 2
Find 5 × \(\frac{3}{10}\) Identify the two whole numbers between which the product lies.

So, 5 × \(\frac{3}{10}\) = ______________.
The product lies between the whole numbers 1 and 2. Look at the product before it was simplified.

Answer:

Equation showing 5 × \(\frac{3}{10}\) is a multiple of \(\frac{1}{10}\) unit fraction is 15 × \(\frac{1}{10}\)
Explanation:
5 × \(\frac{3}{10}\) as unit fraction = ??
=> 5 × \(\frac{3}{10}\)
=> \(\frac{15}{10}\)
=> \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\)+\(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\)+\(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\)+\(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\)
= 15 × \(\frac{1}{10}\)
Talk Math
Does 3 × \(\frac{7}{8}\) = 3\(\frac{7}{8}\)? Explain.

Answer:
Yes, 3 × \(\frac{7}{8}\) = 3\(\frac{7}{8}\) because both the product value is same.
Explanation:
3 × \(\frac{7}{8}\) = \(\frac{7}{8}\) + \(\frac{7}{8}\) + \(\frac{7}{8}\)
= \(\frac{21}{8}\)
= 3\(\frac{7}{8}\) = 3 × \(\frac{7}{8}\) = (3 × 7) ÷ 8 = \(\frac{21}{8}\)
Guided Practice
Multiply.
Question 1.
5 × \(\frac{1}{8}\) = ________________
Answer:
5 multiplied by \(\frac{1}{8}\), we get the product \(\frac{5}{8}\)
Explanation:
Multiplication:
5 × \(\frac{1}{8}\)
= [(5 × 1) ÷ 8]
= \(\frac{5}{8}\)
Question 2.
4 × \(\frac{2}{3}\) = ________________
Answer:
4 multiplied by \(\frac{2}{3}\), we get the product \(\frac{8}{3}\) or 2\(\frac{2}{3}\)
Explanation:
Multiplication:
4 × \(\frac{2}{3}\)
=[(4 × 2) ÷ 3]
= \(\frac{8}{3}\) or 2\(\frac{2}{3}\)
McGraw Hill My Math Grade 4 Chapter 9 Lesson 9 My Homework Answer Key
Practice
Multiply.
Question 1.
3 × \(\frac{2}{5}\) = ________________
Answer:
3 multiplied by \(\frac{2}{5}\), we get the product \(\frac{6}{5}\) or 1\(\frac{1}{5}\)
Explanation:
Multiplication:
3 × \(\frac{2}{5}\)
= [(3 × 2) ÷ 5]
= \(\frac{6}{5}\) or 1\(\frac{1}{5}\)
Question 2.
7 × \(\frac{3}{4}\) = ________________
Answer:
7 multiplied by \(\frac{3}{4}\), we get the product \(\frac{21}{4}\) or 5\(\frac{1}{4}\)
Explanation:
Multiplication:
7 × \(\frac{3}{4}\)
= (7 × 3) ÷ 4
= \(\frac{21}{4}\) or 5\(\frac{1}{4}\)
Question 3.
5 × \(\frac{5}{6}\) = ________________
Answer:
5 multiplied by \(\frac{5}{6}\), we get the product \(\frac{25}{6}\) or 4\(\frac{1}{6}\)
Explanation:
Multiplication:
5 × \(\frac{5}{6}\)
= [(5 × 5) ÷ 6]
= \(\frac{25}{6}\) or 4\(\frac{1}{6}\)
Question 4.
2 × \(\frac{8}{10}\) = ________________
Answer:
2 multiplied by \(\frac{8}{10}\), we get the product \(\frac{8}{5}\) or 1\(\frac{3}{5}\)
Explanation:
Multiplication:
2 × \(\frac{8}{10}\)
= [(2 × 8) ÷ 10]
= \(\frac{16}{10}\) ÷ \(\frac{2}{2}\)
= \(\frac{8}{5}\) or 1\(\frac{3}{5}\)
Question 5.
8 × \(\frac{3}{10}\) = ________________
Answer:
8 multiplied by \(\frac{3}{10}\), we get the product \(\frac{12}{5}\) or 2\(\frac{2}{5}\)
Explanation:
Multiplication:
8 × \(\frac{3}{10}\)
= [(8 × 3) ÷ 10]
= \(\frac{24}{10}\) ÷ \(\frac{2}{2}\)
= \(\frac{12}{5}\) or 2\(\frac{2}{5}\)
Question 6.
6 × \(\frac{5}{8}\) = ________________
Answer:
6 multiplied by \(\frac{5}{8}\), we get the product \(\frac{15}{4}\) or 3\(\frac{3}{4}\)
Explanation:
Multiplication:
6 × \(\frac{5}{8}\)
= [(6 × 5) ÷ 8]
= \(\frac{30}{8}\) ÷ \(\frac{2}{2}\)
= \(\frac{15}{4}\) or 3\(\frac{3}{4}\)
Find each product. Identify the two whole numbers between which the product lies.
Question 7.
5 × \(\frac{7}{10}\) = ________________
The product lies between ______________ and ______________.
Answer:
5 multiplied by \(\frac{7}{10}\), we get the product \(\frac{7}{2}\) or 3\(\frac{1}{2}\)
The product lies between 3 and 4.
Explanation:
5 × \(\frac{7}{10}\)
= [(5 × 7) ÷ 10]
= \(\frac{35}{10}\) ÷ \(\frac{5}{5}\)
= \(\frac{7}{2}\) or 3\(\frac{1}{2}\)
Question 8.
7 × \(\frac{8}{10}\) = ________________
The product lies between ______________ and ______________.
Answer:
7 multiplied by \(\frac{8}{10}\), we get the product \(\frac{28}{5\) or 5\(\frac{3}{5}\)
The product lies between 5 and 6.
Explanation:
Multiplication:
7 × \(\frac{8}{10}\)
= [(7 × 8) ÷ 10]
= \(\frac{56}{10}\) ÷ \(\frac{2}{2}\)
= \(\frac{28}{5\) or 5\(\frac{3}{5}\)
Question 9.
3 × \(\frac{3}{4}\) = ________________
The product lies between ______________ and ______________.
Answer:
3 multiplied by \(\frac{3}{4}\), we get the product \(\frac{9}{4}\) or 2\(\frac{1}{4}\)
The product lies between 2 and 3.
Explanation:
Multiplication:
3 × \(\frac{3}{4}\)
= [(3 × 3) ÷ 4]
= \(\frac{9}{4}\) or 2\(\frac{1}{4}\)
Question 10.
6 × \(\frac{4}{5}\) = ________________
The product lies between ______________ and ______________.
Answer:
6 multiplied by \(\frac{4}{5}\), we get the product \(\frac{24}{5}\) or 4\(\frac{4}{5}\)
The product lies between 6 and 7.
Explanation:
Multiplication:
6 × \(\frac{4}{5}\)
= [(6 × 4) ÷ 5]
= \(\frac{24}{5}\) or 4\(\frac{4}{5}\)
Problem Solving
Question 11.
Mathematical PRACTICE Use Number Sense Calvin’s rug covers \(\frac{1}{8}\) of the floor space in his bedroom. How much floor space would be covered if Calvin had 4 rugs of that size? Write in simplest form.
Answer:
Length of the floor space would be covered by 4 rugs of that size = \(\frac{1}{2}\)
Explanation:
Length of the floor space in his bedroom Calvin’s rug covers = \(\frac{1}{8}\)
Number of rugs = 4.
Length of the floor space would be covered by 4 rugs of that size = Number of rugs × Length of the floor space in his bedroom Calvin’s rug covers
= 4 × \(\frac{1}{8}\)
= [(4 × 1) ÷ 8]
= \(\frac{4}{8}\) ÷ \(\frac{4}{4}\)
= \(\frac{1}{2}\)
Question 12.
Amy uses \(\frac{2}{3}\) of a yard of fabric for each pillow she makes. How many yards of fabric will she need in order to make 8 pillows? Write in simplest form.
Answer:
Number of yards of fabric will she need in order to make 8 pillows = \(\frac{16}{3}\) or 5\(\frac{1}{3}\)
Explanation:
Number of a yard of fabric for each pillow she makes Amy uses = \(\frac{2}{3}\)
Number of pillows = 8.
Number of yards of fabric will she need in order to make 8 pillows = Number of pillows × Number of a yard of fabric for each pillow she makes Amy uses
= 8 × \(\frac{2}{3}\)
= [(8 × 2) ÷ 3]
= \(\frac{16}{3}\) or 5\(\frac{1}{3}\)
Test Practice
Question 13.
Sheila eats \(\frac{3}{4}\) of a bag of baby carrots each week. How many bags of baby carrots does she eat in 6 weeks? Write in simplest form.
(A) 4\(\frac{1}{2}\) bags
(B) 3 bags
(C) 2\(\frac{1}{4}\) bags
(D) 1\(\frac{1}{2}\) bags
Answer:
Number of bags of baby carrots she eats in 6 weeks = \(\frac{9{2}\) or 4\(\frac{1}{2}\)(A) 4\(\frac{1}{2}\) bags
Explanation:
Number of a bag of baby carrots each week Sheila eats = \(\frac{3}{4}\)
Number of weeks = 6.
Number of bags of baby carrots she eats in 6 weeks = Number of weeks × Number of a bag of baby carrots each week Sheila eats
= 6 × \(\frac{3}{4}\)
= [(6 × 3) ÷ 4]
= \(\frac{18{4}\) ÷ \(\frac{2}{2}\)
= \(\frac{9{2}\) or 4\(\frac{1}{2}\)