All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 9 Lesson 8 Model Fractions and Multiplication will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 4 Answer Key Chapter 9 Lesson 8 Model Fractions and Multiplication
You have learned to write a fraction as a sum of unit fractions. For example, \(\frac{4}{5}\) = \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\).
You can also write a fraction as a multiple of a unit fraction.
Build It
Use an equation to write \(\frac{4}{5}\) as a multiple of a unit fraction.
One Way:
Use fraction tiles.
Model \(\frac{4}{5}\) using fraction tiles. Draw your result below.
How many \(\frac{1}{5}\)-tiles did you use?

Another Way:
Use repeated addition.
You know that \(\frac{4}{5}\) = \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\)
How many times is added to equal \(\frac{4}{5}\)?
So, \(\frac{4}{5}\) = ________________ × \(\frac{1}{5}\).
Answer:
\(\frac{4}{5}\) = 4 × \(\frac{1}{5}\).
Explanation:
\(\frac{4}{5}\) as a multiple of a unit fraction = ??
1. Use fraction tiles:
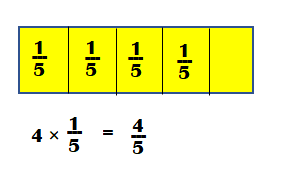
2. Use repeated addition:
You know that \(\frac{4}{5}\) = \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\)
=> 4 times \(\frac{1}{5}\) is added to equal \(\frac{4}{5}\).
You know that 6 is a multiple of 2. Any multiples of 6, such as 12, 18, and 24, are also multiples of 2. The same is true for fractions. A multiple of a fraction can also be written as a multiple of a unit fraction.
Try It
Use an equation to write 2 × \(\frac{4}{5}\) as a multiple of a unit fraction.

Use repeated addition to write 2 × \(\frac{4}{5}\) as \(\frac{4}{5}\) + \(\frac{4}{5}\).
\(\frac{4}{5}\) + \(\frac{4}{5}\) = \(\frac{8}{5}\) Add like fractions.
Model \(\frac{8}{5}\) using fraction tiles. Draw your result below.
How many \(\frac{1}{5}\)-tiles did you use? ______________
So, \(\frac{8}{5}\) is a multiple of \(\frac{4}{5}\). It is also a multiple of \(\frac{1}{5}\).
\(\frac{8}{5}\) = ________________ × \(\frac{1}{5}\)
Write an equation showing that \(\frac{8}{5}\) is a multiple of the unit fraction \(\frac{1}{5}\).
\(\frac{8}{5}\) = ________________ × \(\frac{1}{5}\)
So, 2 × \(\frac{4}{5}\) = ________________ × \(\frac{1}{5}\).
Answer:
Equation showing that \(\frac{8}{5}\) is a multiple of the unit fraction \(\frac{1}{5}\) is
2 × \(\frac{4}{5}\) = 8 × \(\frac{1}{5}\).
Explanation:
2 × \(\frac{4}{5}\) as a multiple of a unit fraction = ??
1. Use fraction tiles:
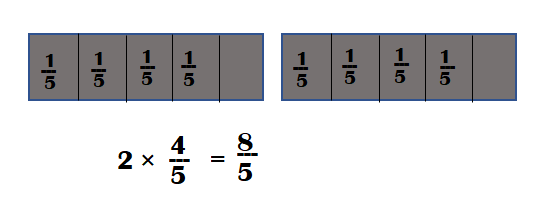
2 × \(\frac{4}{5}\) = \(\frac{4}{5}\) + \(\frac{4}{5}\) = \(\frac{8}{5}\)
2. Use repeated addition:
2 × \(\frac{4}{5}\) = \(\frac{4}{5}\) + \(\frac{4}{5}\).
=> \(\frac{4}{5}\) + \(\frac{4}{5}\) = \(\frac{8}{5}\)
So, \(\frac{8}{5}\) is a multiple of \(\frac{4}{5}\). It is also a multiple of \(\frac{1}{5}\).
\(\frac{8}{5}\) = 8 × \(\frac{1}{5}\)
Talk About It
Question 1.
Mathematical PRACTICE Identify Structure Write an equation showing how \(\frac{3}{8}\) is a multiple of \(\frac{1}{8}\).
Answer:
Equation showing \(\frac{3}{8}\) is a multiple of \(\frac{1}{8}\) is \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\)
Explanation:
\(\frac{3}{8}\) is a multiple of \(\frac{1}{8}\):
=> \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\)
=> (1 + 1 + 1) ÷ 8
=> \(\frac{3}{8}\)
Question 2.
Write equations showing how \(\frac{6}{8}\) is a multiple of both \(\frac{3}{8}\) and \(\frac{1}{8}\).
Answer:
Equations showing \(\frac{6}{8}\) is a multiple of both \(\frac{3}{8}\) and \(\frac{1}{8}\) is 2 × \(\frac{3}{8}\) = 6 × \(\frac{1}{8}\)
Explanation:
\(\frac{6}{8}\) is a multiple of both \(\frac{3}{8}\) and \(\frac{1}{8}\):
1. \(\frac{6}{8}\) is a multiple of both \(\frac{3}{8}\)
=> \(\frac{3}{8}\) + \(\frac{3}{8}\)
=> (3 + 3) ÷ 8
=> \(\frac{6}{8}\)
2. \(\frac{6}{8}\) is a multiple of \(\frac{1}{8}\):
=> \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\)+ \(\frac{1}{8}\)+\(\frac{1}{8}\) + \(\frac{1}{8}\)
=> (1 + 1 + 1 + 1 + 1 + 1) ÷ 8
=> \(\frac{6}{8}\)
Practice It
Algebra Use an equation to write each fraction or product as a multiple of a unit fraction.
Question 3.
\(\frac{3}{4}\) ________________
Answer:
Equation showing \(\frac{3}{4}\) as a multiple of a \(\frac{1}{4}\) unit fraction is
\(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\)
Explanation:
\(\frac{3}{4}\) as a multiple of a unit fraction:
=> \(\frac{1}{4}\) + \(\frac{1}{4}\)+ \(\frac{1}{4}\)
=> (1 + 1 +1) ÷ 4
=> \(\frac{3}{4}\)
Question 4.
\(\frac{7}{8}\) ________________
Answer:
Equation showing \(\frac{7}{8}\) as a multiple of a \(\frac{1}{8}\) unit fraction is 7 × \(\frac{1}{8}\)
Explanation:
\(\frac{7}{8}\) as a multiple of a unit fraction:
=> \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\)+ \(\frac{1}{8}\)+ \(\frac{1}{8}\)+ \(\frac{1}{8}\)+ \(\frac{1}{8}\)
=> (1 + 1 + 1 + 1 + 1 + 1 + 1) ÷ 8
=> \(\frac{7}{8}\)
Question 5.
\(\frac{5}{12}\) ________________
Answer:
Equation showing \(\frac{5}{12}\) as a multiple of a \(\frac{1}{12}\) unit fraction is 5 × \(\frac{1}{12}\)
Explanation:
\(\frac{5}{12}\) as a multiple of a unit fraction:
=> \(\frac{1}{12}\) + \(\frac{1}{12}\) + \(\frac{1}{12}\)+ \(\frac{1}{12}\)+ \(\frac{1}{12}\)
=> (1 + 1 + 1 + 1 + 1) ÷ 12
=> \(\frac{5}{12}\)
Question 6.
\(\frac{5}{6}\) ________________
Answer:
Equation showing \(\frac{5}{6}\) as a multiple of a \(\frac{1}{6}\) unit fraction is 5 × \(\frac{1}{6}\)
Explanation:
Equation showing \(\frac{5}{6}\) as a multiple of a unit fraction:
=> \(\frac{1}{6}\) + \(\frac{1}{6}\)+ \(\frac{1}{6}\)+ \(\frac{1}{6}\)+\(\frac{1}{6}\)
=> (1 + 1 + 1 + 1 + 1) ÷ 6
=> \(\frac{5}{6}\)
Question 7.
2 × \(\frac{2}{3}\) ________________
Answer:
Equation showing 2 × \(\frac{2}{3}\) as a multiple of a \(\frac{1}{3}\) and \(\frac{2}{3}\) unit fraction is 4 × \(\frac{1}{3}\) = 2 × \(\frac{2}{3}\)
Explanation:
2 × \(\frac{2}{3}\) as a multiple of a unit fraction:
=> \(\frac{1}{3}\) + \(\frac{1}{3}\) + \(\frac{1}{3}\) + \(\frac{1}{3}\)
=> 4 × \(\frac{1}{3}\) or 2 × \(\frac{2}{3}\)
Question 8.
2 × \(\frac{5}{6}\) ________________
Answer:
Equation showing 2 × \(\frac{5}{6}\) as a multiple of a \(\frac{5}{6}\) and \(\frac{1}{6}\) is \(\frac{5}{6}\) + \(\frac{5}{6}\) = 10 × \(\frac{1}{6}\)
Explanation:
2 × \(\frac{5}{6}\) as a multiple of a unit fraction:
=> \(\frac{5}{6}\)+ \(\frac{5}{6}\)
=> \(\frac{10}{6}\)
= \(\frac{1}{6}\) + \(\frac{1}{6}\)+\(\frac{1}{6}\)+ \(\frac{1}{6}\)+ \(\frac{1}{6}\)+ \(\frac{1}{6}\)+ \(\frac{1}{6}\)+ \(\frac{1}{6}\)+ \(\frac{1}{6}\) + \(\frac{1}{6}\)
=> 10 × \(\frac{1}{6}\)
=> 10\(\frac{1}{6}\)
Question 9.
4 × \(\frac{3}{4}\) ________________
Answer:
Equation showing 4 × \(\frac{3}{4}\) as a multiple of a \(\frac{3}{4}\) unit fraction is \(\frac{3}{4}\) + \(\frac{3}{4}\)+ \(\frac{3}{4}\)+\(\frac{3}{4}\)
Explanation:
4 × \(\frac{3}{4}\) as a multiple of a unit fraction:
=>\(\frac{3}{4}\) + \(\frac{3}{4}\)+ \(\frac{3}{4}\)+\(\frac{3}{4}\)
=> (3 + 3 + 3 + 3) ÷ 4
=> 12 ÷ 4 or \(\frac{12}{4}\)
Question 10.
3 × \(\frac{7}{8}\) ________________
Answer:
Equation showing 3 × \(\frac{7}{8}\) as a multiple of a \(\frac{7}{8}\) unit fraction is \(\frac{7}{8}\) + \(\frac{7}{8}\) + \(\frac{7}{8}\)
Explanation:
3 × \(\frac{7}{8}\) as a multiple of a unit fraction:
=> \(\frac{7}{8}\) + \(\frac{7}{8}\) + \(\frac{7}{8}\)
=> (7 + 7 + 7) ÷ 8
=> 21 ÷ 8 or \(\frac{21}{8}\)
Question 11.
5 × \(\frac{3}{5}\) ________________
Answer:
Equation showing 5 × \(\frac{3}{5}\) as a multiple of a \(\frac{3}{5}\) unit fraction is \(\frac{3}{5}\) + \(\frac{3}{5}\) + \(\frac{3}{5}\)+ \(\frac{3}{5}\)+ \(\frac{3}{5}\)
Explanation:
5 × \(\frac{3}{5}\) as a multiple of a unit fraction:
=> \(\frac{3}{5}\) + \(\frac{3}{5}\) + \(\frac{3}{5}\)+ \(\frac{3}{5}\)+ \(\frac{3}{5}\)
=> (3 + 3 + 3 + 3 + 3) ÷ 5
=\(\frac{15}{5}\)
Question 12.
6 × \(\frac{7}{12}\) ________________
Answer:
Equation showing 6 × \(\frac{7}{12}\) as a multiple of a \(\frac{7}{12}\) unit fraction is \(\frac{7}{12}\) + \(\frac{7}{12}\) + \(\frac{7}{12}\) + \(\frac{7}{12}\) +\(\frac{7}{12}\) + \(\frac{7}{12}\)
Explanation:
6 × \(\frac{7}{12}\) as a multiple of a unit fraction:
=> \(\frac{7}{12}\) + \(\frac{7}{12}\) + \(\frac{7}{12}\) + \(\frac{7}{12}\) +\(\frac{7}{12}\) + \(\frac{7}{12}\)
=> (7 + 7 + 7 + 7 + 7 + 7) ÷ 12
=> \(\frac{42}{12}\)
Apply It
Question 13.
Mathematical PRACTICE Model Math Use fraction tiles and repeated addition to write 3 × \(\frac{3}{4}\) as a multiple of a unit fraction. Draw your result below.

Answer:
Equation showing 3 × \(\frac{3}{4}\) as a multiple of a \(\frac{1}{4}\) unit fraction is 9 × \(\frac{1}{4}\)
Explanation:
3 × \(\frac{3}{4}\) as a multiple of a unit fraction.
=> \(\frac{1}{4}\) + \(\frac{1}{4}\)+ \(\frac{1}{4}\)+ \(\frac{1}{4}\)+ \(\frac{1}{4}\)+ \(\frac{1}{4}\)+ \(\frac{1}{4}\)+\(\frac{1}{4}\) + \(\frac{1}{4}\)
=> (1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1) ÷ 4
=> \(\frac{9}{4}\)
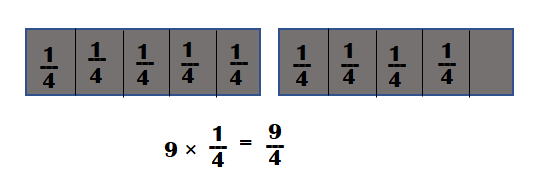
Question 14.
Gracie and Jackson each bought \(\frac{2}{3}\) pound of blackberries. Circle the correct equation that represents 2 × \(\frac{2}{3}\) as a multiple of a unit fraction.
2 × \(\frac{2}{3}\) = 4 × \(\frac{1}{3}\)
2 × \(\frac{2}{3}\) = 2 × \(\frac{1}{3}\)
Answer:
2 × \(\frac{2}{3}\) as a multiple of a \(\frac{1}{3}\) unit fraction is 4 × \(\frac{1}{3}\).
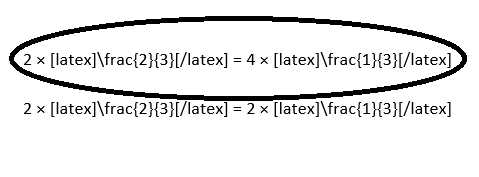
Explanation:
Number of pound of blackberries Gracie and Jackson each bought = \(\frac{2}{3}\) .
2 × \(\frac{2}{3}\) as a multiple of a unit fraction = ??
=> \(\frac{2}{3}\) + \(\frac{2}{3}\)
=> (2 + 2) ÷ 3
=> \(\frac{4}{3}\)
=> \(\frac{1}{3}\) + \(\frac{1}{3}\) + \(\frac{1}{3}\) +\(\frac{1}{3}\)
=> 4 × \(\frac{1}{3}\)
Question 15.
Mathematical PRACTICE Use Algebra Find the unknown in the equation
m × \(\frac{1}{6}\) = \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\).
Answer:
Unknown in the equation m × \(\frac{1}{6}\) = \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) is 5.
Explanation:
Equation given:
m × \(\frac{1}{6}\) = \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\).
=> m = ??
=> m × \(\frac{1}{6}\) = \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\)
=> m × \(\frac{1}{6}\) = (1 + 1 + 1 + 1 + 1) ÷ 6
=> m × \(\frac{1}{6}\) = 5 × \(\frac{1}{6}\)
=> m = {5 × \(\frac{1}{6}\)} ÷ 5 × \(\frac{1}{6}\)
=> m = 5.
Write About It
Question 16.
How can any fraction \(\frac{a}{b}\) be written as a multiple of a unit fraction?
Answer:
Any fraction \(\frac{a}{b}\) be written as a multiple of a unit fraction by using the number of times the unit fraction holds to express the given fraction.
McGraw Hill My Math Grade 4 Chapter 9 Lesson 8 My Homework Answer Key
Practice
Algebra Use an equation to write each fraction as a multiple of a unit fraction.
Question 1.
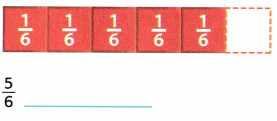
Answer:
Equation showing \(\frac{5}{6}\) as a multiple of a \(\frac{1}{6}\) unit fraction is 5 × \(\frac{1}{6}\)
Explanation:
Equation showing to the above fraction tiles:
\(\frac{1}{6}\) + \(\frac{1}{6}\)+ \(\frac{1}{6}\)+ \(\frac{1}{6}\)+ \(\frac{1}{6}\)
=> (1 + 1 + 1 + 1 + 1) ÷ 6
=> 5 × \(\frac{1}{6}\)
Question 2.
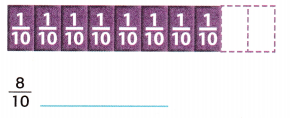
Answer:
Equation showing \(\frac{8}{10}\) as a multiple of a \(\frac{1}{10}\) unit fraction is 8 × \(\frac{1}{10}\)
Explanation:
Equation showing to the above fraction tiles:
\(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\)
=> (1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 ) ÷ 10
=> 8 × \(\frac{1}{10}\)
Algebra Use an equation to write each fraction or product as a multiple of a unit fraction.
Question 3.
\(\frac{3}{8}\) ___________________
Answer:
Equation showing \(\frac{3}{8}\) as a multiple of a \(\frac{1}{8}\) unit fraction is 3 × \(\frac{1}{8}\)
Explanation:
\(\frac{3}{8}\) = \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\)
= 3 × \(\frac{1}{8}\)
Question 4.
\(\frac{7}{12}\) ___________________
Answer:
Equation showing \(\frac{7}{12}\) as a multiple of a \(\frac{1}{12}\) unit fraction is 7 × \(\frac{1}{12}\)
Explanation:
\(\frac{7}{12}\) = \(\frac{1}{12}\) + \(\frac{1}{12}\) + \(\frac{1}{12}\) + \(\frac{1}{12}\) + \(\frac{1}{12}\) + \(\frac{1}{12}\) + \(\frac{1}{12}\)
= (1 + 1 + 1 + 1 + 1 + 1 + 1) ÷ 12
= 7 × \(\frac{1}{12}\)
Question 5.
\(\frac{6}{10}\) ___________________
Answer:
Equation showing \(\frac{6}{10}\) as a multiple of a \(\frac{1}{10}\) unit fraction is 6 × \(\frac{1}{10}\)
Explanation:
\(\frac{6}{10}\) = \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\)
= (1 + 1 + 1 + 1 + 1 + 1) ÷ 10
= 6 × \(\frac{1}{10}\)
Question 6.
\(\frac{4}{5}\) ___________________
Answer:
Equation showing \(\frac{4}{5}\) as a multiple of a \(\frac{1}{5}\) unit fraction is 4 × \(\frac{1}{5}\)
Explanation:
\(\frac{4}{5}\) = \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\)
= (1 + 1 + 1 + 1) ÷ 5
= 4 × \(\frac{1}{5}\)
Question 7.
3 × \(\frac{4}{5}\) ___________________
Answer:
Equation showing 3 × \(\frac{4}{5}\) as a multiple of a \(\frac{1}{5}\) unit fraction is 12 × \(\frac{1}{5}\)
Explanation:
3 × \(\frac{4}{5}\) = \(\frac{12}{5}\) = \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\)
= 12 × \(\frac{1}{5}\)
Question 8.
5 × \(\frac{2}{5}\) ___________________
Answer:
Equation showing 5 × \(\frac{2}{5}\) as a multiple of a \(\frac{1}{5}\) unit fraction is 10 × \(\frac{1}{5}\)
Explanation:
5 × \(\frac{2}{5}\) = \(\frac{10}{5}\) = \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\)
= 10 × \(\frac{1}{5}\)
Question 9.
8 × \(\frac{6}{10}\) ___________________
Answer:
Equation showing 8 × \(\frac{6}{10}\) as a multiple of a \(\frac{8}{10}\) unit fraction is 6 × \(\frac{8}{10}\)
Explanation:
8 × \(\frac{6}{10}\) = \(\frac{48}{10}\) = \(\frac{8}{10}\) + \(\frac{8}{10}\) + \(\frac{8}{10}\)+ \(\frac{8}{10}\) + \(\frac{8}{10}\)+ \(\frac{8}{10}\)
= 6 × \(\frac{8}{10}\)
Question 10.
7 × \(\frac{8}{12}\) ___________________
Answer:
Equation showing 7 × \(\frac{8}{12}\) as a multiple of a \(\frac{7}{12}\) unit fraction is 8 × \(\frac{7}{12}\)
Explanation:
7 × \(\frac{8}{12}\) = \(\frac{56}{12}\) = \(\frac{7}{12}\) + \(\frac{7}{12}\) + \(\frac{7}{12}\) + \(\frac{7}{12}\) + \(\frac{7}{12}\) + \(\frac{7}{12}\) + \(\frac{7}{12}\) + \(\frac{7}{12}\)
= 8 × \(\frac{7}{12}\)
Problem Solving
Question 11.
Mathematical PRACTICE Model Math Marcia has one cup of tea each day for 7 days. She puts \(\frac{2}{3}\) tablespoons of honey in each cup of tea. Write an equation that represents 7 × \(\frac{2}{3}\) as a multiple of a unit fraction.
Answer:
Equation that represents 7 × \(\frac{2}{3}\) as a multiple of a \(\frac{1}{3}\) unit fraction is 14 × \(\frac{1}{3}\)
Explanation:
Number of days Marcia has one cup of tea = 7.
Number of cups of tea he has each day = 1.
Number of tablespoons of honey in each cup of tea she puts = \(\frac{2}{3}\).
Total number of tea with tablespoons of honey he has = Number of days Marcia has one cup of tea × Number of cups of tea he has each day × Number of tablespoons of honey in each cup of tea she puts
= 7 × 1 × \(\frac{2}{3}\)
= \(\frac{14}{3}\)
= \(\frac{1}{3}\) + \(\frac{1}{3}\) + \(\frac{1}{3}\) + \(\frac{1}{3}\) + \(\frac{1}{3}\)+ \(\frac{1}{3}\)+ \(\frac{1}{3}\)+ \(\frac{1}{3}\)+ \(\frac{1}{3}\)+\(\frac{1}{3}\)+ \(\frac{1}{3}\)+\(\frac{1}{3}\)+\(\frac{1}{3}\) + \(\frac{1}{3}\)
= 14 × \(\frac{1}{3}\)
Question 12.
Sam buys 4 tropical fish. Each fish is \(\frac{5}{8}\) of an inch long. Write an equation that represents 4 × \(\frac{5}{8}\) as a multiple of a unit fraction.
Answer:
Equation that represents 4 × \(\frac{5}{8}\) as a multiple of a \(\frac{5}{8}\) unit fraction is \(\frac{5}{8}\) + \(\frac{5}{8}\)+ \(\frac{5}{8}\)+ \(\frac{5}{8}\)
Explanation:
Number of tropical fish Sam buys = 4.
Number of inches each fish = \(\frac{5}{8}\)
Total number of inches all fishes = Number of tropical fish Sam buys × Number of inches each fish
= 4 × \(\frac{5}{8}\)
=> \(\frac{20}{8}\)