All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 9 Review will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 4 Chapter 9 Review Answer Key
Vocabulary Check
Question 1.
Use the numbers on the number cubes to create each type of fraction listed below. You can use the numbers more than once.
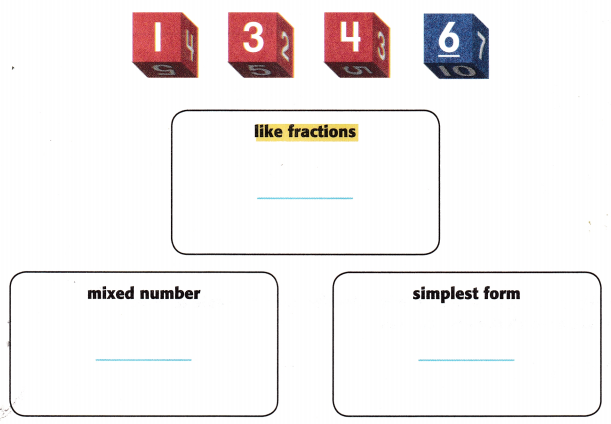
Answer:
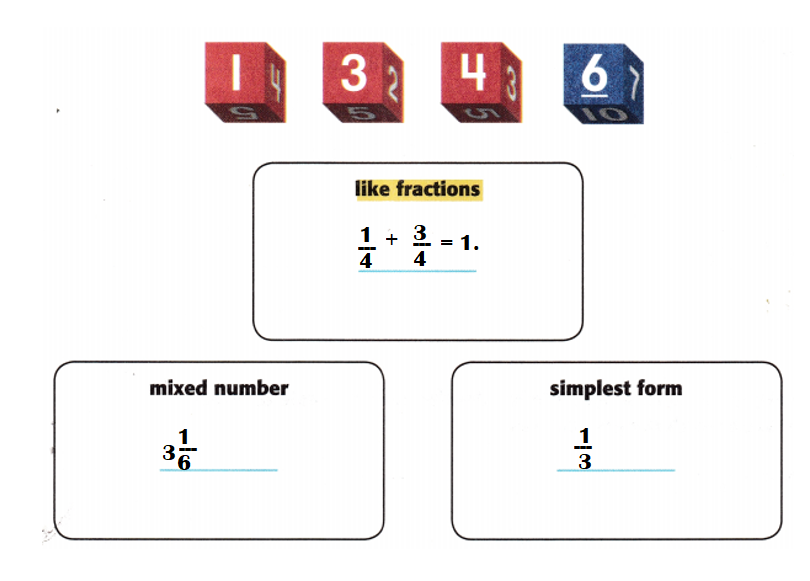
Explanation:
The group of two or more fractions that have exactly the same denominator are called like fractions.
=> \(\frac{1}{4}\) + \(\frac{3}{4}\) = 1.
A mixed number is a number consisting of a whole number and a proper fraction.
=>3\(\frac{1}{6}\)
A fraction is in simplest form if the top and bottom have no common factors other than 1. In other words, you cannot divide the top and bottom any further and have them still be whole numbers.
=> \(\frac{1}{3}\)
Concept Check
Find each sum. Write in simplest form.
Question 2.
\(\frac{1}{6}\) + \(\frac{4}{6}\) = _________________
Answer:
Sum of \(\frac{1}{6}\) and \(\frac{4}{6}\), we get \(\frac{5}{6}\)
Explanation:
\(\frac{1}{6}\) + \(\frac{4}{6}\)
=> [(1 + 4) ÷ 6]
=> \(\frac{5}{6}\)
Question 3.
3\(\frac{3}{5}\) + 2\(\frac{1}{5}\) = _________________
Answer:
Sum of 3\(\frac{3}{5}\) and 2\(\frac{1}{5}\), we get \(\frac{29}{5}\) or 5\(\frac{4}{5}\)
Explanation:
3\(\frac{3}{5}\) + 2\(\frac{1}{5}\)
= {[(3 × 5) + 3] ÷ 5} + {[(2 × 5) + 1] ÷ 5}
= [(15 + 3) ÷ 5] + [(10 + 1) ÷ 5]
= \(\frac{18}{5}\) + \(\frac{11}{5}\)
= [(18 + 11) ÷ 5]
= \(\frac{29}{5}\) or 5\(\frac{4}{5}\)
Question 4.
\(\frac{2}{8}\) + \(\frac{4}{8}\) = _________________
Answer:
Sum of \(\frac{2}{8}\) and \(\frac{4}{8}\), we get \(\frac{3}{4}\)
Explanation:
\(\frac{2}{8}\) + \(\frac{4}{8}\)
= [(2 + 4) ÷ 8]
= \(\frac{6}{8}\) ÷ \(\frac{2}{2}\)
= \(\frac{3}{4}\)
Find each difference. Write in simplest form.
Question 5.
\(\frac{3}{4}\) – \(\frac{2}{4}\) = ________________
Answer:
Difference between \(\frac{3}{4}\) and \(\frac{2}{4}\), we get \(\frac{1}{4}\)
Explanation:
\(\frac{3}{4}\) – \(\frac{2}{4}\)
= [(3 – 2) ÷ 4]
= \(\frac{1}{4}\)
Question 6.
5\(\frac{2}{3}\) – 2\(\frac{1}{3}\) = ________________
Answer:
Difference between 5\(\frac{2}{3}\) and 2\(\frac{1}{3}\), we get \(\frac{10}{3}\) or 3\(\frac{1}{3}\)
Explanation:
5\(\frac{2}{3}\) – 2\(\frac{1}{3}\)
= {[(5 × 3) + 2] ÷ 3} – {[(2 × 3) + 1] ÷ 3}
= [(15 + 2) ÷ 3] – [(6 + 1) ÷ 3]
= \(\frac{17}{3}\) – \(\frac{7}{3}\)
= [(17 – 7) ÷ 3]
= \(\frac{10}{3}\) or 3\(\frac{1}{3}\)
Question 7.
\(\frac{8}{10}\) – \(\frac{3}{10}\) = _________________
Answer:
Difference between \(\frac{8}{10}\) and \(\frac{3}{10}\), we get \(\frac{1}{2}\)
Explanation:
\(\frac{8}{10}\) – \(\frac{3}{10}\)
= [(8 – 3) ÷ 10]
= \(\frac{5}{10}\) ÷ \(\frac{5}{5}\)
= \(\frac{1}{2}\)
Algebra Use an equation to write each fraction or product as a multiple of a unit fraction.
Question 8.
\(\frac{3}{5}\) __________________
Answer:
\(\frac{3}{5}\) as a multiple of a \(\frac{1}{5}\) unit fraction, we get 3 × \(\frac{1}{5}\)
Explanation:
\(\frac{3}{5}\) unit fraction = ??
=> \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\)
=> 3 × \(\frac{1}{5}\)
Question 9.
\(\frac{9}{10}\) __________________
Answer:
\(\frac{9}{10}\) as a multiple of a \(\frac{1}{10}\) unit fraction, we get 9 × \(\frac{1}{10}\)
Explanation:
\(\frac{9}{10}\) unit fraction = ??
=> \(\frac{9}{10}\) = \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\)
= 9 × \(\frac{1}{10}\)
Question 10.
\(\frac{8}{12}\) ________________
Answer:
\(\frac{8}{12}\) as a multiple of a \(\frac{1}{12}\) unit fraction, we get 8 × \(\frac{1}{12}\)
Explanation:
\(\frac{8}{12}\) unit fraction = ??
=> \(\frac{8}{12}\) = \(\frac{1}{12}\) + \(\frac{8}{12}\) + \(\frac{1}{12}\) + \(\frac{8}{12}\)+ \(\frac{1}{12}\) + \(\frac{8}{12}\) + \(\frac{1}{12}\) + \(\frac{8}{12}\)
= 8 × \(\frac{1}{12}\)
Question 11.
\(\frac{7}{8}\) _________________
Answer:
\(\frac{7}{8}\) as a multiple of a \(\frac{1}{8}\) unit fraction, we get 7 × \(\frac{1}{8}\)
Explanation:
\(\frac{7}{8}\) unit fraction = ??
=> \(\frac{7}{8}\) = \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\)
= 7 × \(\frac{1}{8}\)
Question 12.
4 × \(\frac{3}{5}\) _________________
Answer:
4 × \(\frac{3}{5}\) as a multiple of a \(\frac{1}{5}\) unit fraction, we get 12 × \(\frac{1}{5}\)
Explanation:
4 × \(\frac{3}{5}\) unit fraction = ??
=> 4 × \(\frac{3}{5}\) = \(\frac{3}{5}\) + \(\frac{3}{5}\)+ \(\frac{3}{5}\)+ \(\frac{3}{5}\)
=> [(3 + 3 + 3 +3) ÷ 5]
=> \(\frac{12}{5}\)
=> 12 × \(\frac{1}{5}\)
Question 13.
2 × \(\frac{9}{10}\) _________________
Answer:
2 × \(\frac{9}{10}\) as a multiple of a \(\frac{1}{5}\) unit fraction, we get 9 × \(\frac{1}{5}\)
Explanation:
2 × \(\frac{9}{10}\) unit fraction = ??
=> 2 × \(\frac{9}{10}\)
=> \(\frac{9}{10}\) + \(\frac{9}{10}\)
=> [(9 + 9) ÷ 10]
=> \(\frac{18}{10}\) ÷ \(\frac{2}{2}\)
=> \(\frac{9}{5}\)
=> 9 × \(\frac{1}{5}\)
Question 14.
3 × \(\frac{8}{12}\) __________________
Answer:
3 × \(\frac{8}{12}\) as a multiple of a \(\frac{8}{12}\) unit fraction, we get 2.
Explanation:
3 × \(\frac{8}{12}\) unit fraction = ??
=> \(\frac{8}{12}\) + \(\frac{8}{12}\) + \(\frac{8}{12}\)
=> [(8 + 8 + 8) ÷ 12]
=> \(\frac{24}{12}\) ÷ \(\frac{12}{12}\)
=> \(\frac{2}{1}\)
=> 2.
Question 15.
6 × \(\frac{7}{8}\) ___________________
Answer:
6 × \(\frac{7}{8}\) as a multiple of a \(\frac{1}{4}\) unit fraction, we get 5\(\frac{1}{4}\)
Explanation:
6 × \(\frac{7}{8}\) unit fraction = ??
=> 6 × \(\frac{7}{8}\)
=> [(6 × 7) ÷ 8]
=> \(\frac{42}{8}\) ÷ \(\frac{2}{2}\)
=> \(\frac{21}{4}\) or 5\(\frac{1}{4}\)
Multiply. Write in simplest form. Identify the two whole numbers between which the product lies.
Question 16.
6 × \(\frac{1}{4}\) ___________________
Answer:
6 multiplied by \(\frac{1}{4}\), we get the product \(\frac{3}{2}\) or 1\(\frac{1}{2}\)
Explanation:
6 × \(\frac{1}{4}\)
= [(6 × 1) ÷ 4]
= \(\frac{6}{4}\) ÷ \(\frac{2}{2}\)
= \(\frac{3}{2}\) or 1\(\frac{1}{2}\)
Question 17.
24 × \(\frac{1}{5}\) ___________________
Answer:
24 multiplied by \(\frac{1}{5}\), we get the product \(\frac{24}{5}\) or 4\(\frac{4}{5}\)
Explanation:
24 × \(\frac{1}{5}\)
= [(24 × 1) ÷ 5]
= \(\frac{24}{5}\) or 4\(\frac{4}{5}\)
Question 18.
7 × \(\frac{3}{5}\) ___________________
Answer:
7 multiplied by \(\frac{3}{5}\), we get the product \(\frac{21}{5}\) or 4\(\frac{1}{5}\)
Explanation:
7 × \(\frac{3}{5}\)
= [(7 × 3) ÷ 5]
= \(\frac{21}{5}\) or 4\(\frac{1}{5}\)
Question 19.
3 × \(\frac{4}{6}\) ___________________
Answer:
3 multiplied by \(\frac{4}{6}\), we get the product 2.
Explanation:
3 × \(\frac{4}{6}\)
= [(3 × 4) ÷ 6]
= \(\frac{12}{6}\) ÷ \(\frac{6}{6}\)
= \(\frac{2}{1}\)
= 2.
Problem Solving
Question 20.
Kylie and her two sisters each have \(\frac{1}{4}\) cup of chopped pineapple. How much pineapple do they have in all?

Answer:
Number of pineapple do they have in all = \(\frac{1}{2}\)
Explanation:
Number of sisters = 2.
Number of cups of chopped pineapple each sister have = \(\frac{1}{4}\)
Number of pineapple do they have in all = Number of sisters × Number of cups of chopped pineapple each sister have
= 2 × \(\frac{1}{4}\)
= [(2 × 1) ÷ 4]
= \(\frac{2}{4}\) ÷ \(\frac{2}{2}\)
= \(\frac{1}{2}\)
Question 21.
Joshua and his four friends each have \(\frac{1}{2}\) package of crackers. How many packages of crackers do they have in all? Explain.
Answer:
Total number of packages of crackers do they have in all = 2.
Explanation:
Number of friends = 4.
Number of package of crackers each friend have = \(\frac{1}{2}\)
Total number of packages of crackers do they have in all = Number of friends × Number of package of crackers each friend have
= 4 × \(\frac{1}{2}\)
= [(4 × 1) ÷ 2]
= \(\frac{4}{2}\) ÷ \(\frac{2}{2}\)
= \(\frac{2}{1}\)
= 2.
Question 22.
Write a real-world problem to add like fractions. Then solve the problem.
Answer:
If a pizza is divided into two equal parts, then each part is equal to half of the whole pizza, its a real -world problem to add like fractions.
Explanation:
In real life, we will many examples of fractions, such as:
If a pizza is divided into two equal parts, then each part is equal to half of the whole pizza.
Number of pizza = 1.
Number of parts pizza divided = 2.
Size of each slice of pizza = Number of pizza ÷ Number of parts pizza divided
= 1 ÷ 2 or \(\frac{1}{2}\)
Test Practice
Question 23.
There are 35 students in Miss Klempa’s class. Suppose each student has \(\frac{1}{10}\) of a box of pencils. How many boxes of pencils do they have in all?
(A) 3 boxes
(B) boxes
(C) 4 boxes
(D) 3\(\frac{1}{2}\) boxes
Answer:
Number of boxes of pencils they have in all = \(\frac{7}{2}\) or 3\(\frac{1}{2}\)
(D) 3\(\frac{1}{2}\) boxes
Explanation:
Number of students in Miss Klempa’s class = 35
Number of a box of pencils each student has = \(\frac{1}{10}\)
Number of boxes of pencils they have in all = Number of students in Miss Klempa’s class × Number of a box of pencils each student has
= 35 × \(\frac{1}{10}\)
= [(35 × 1) ÷ 10
= \(\frac{35}{10}\) ÷ \(\frac{5}{5}\)
= \(\frac{7}{2}\) or 3\(\frac{1}{2}\)
Reflect
Use what you learned about using operations with fractions to complete the graphic organizer.
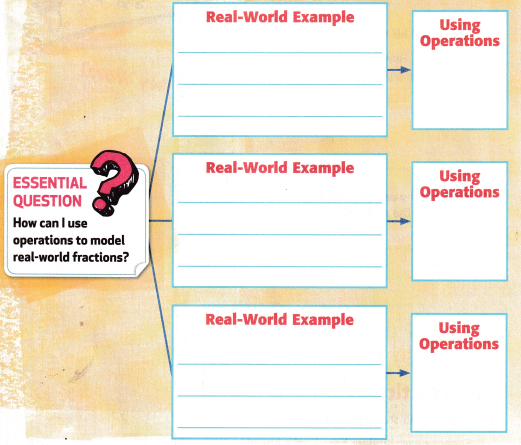
Reflect on the ESSENTIAL QUESTION ? Write your answer below.
Answer:
We can use the four operations (addition, subtraction, multiplication and division) to solve real-world problems.
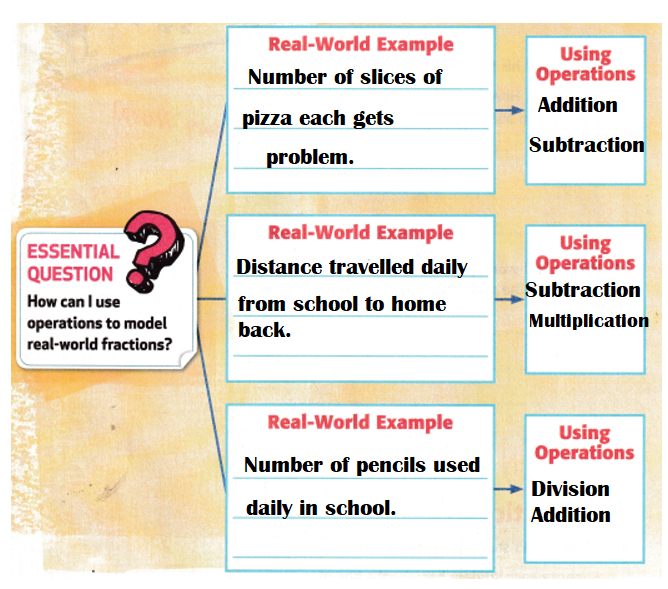
Explanation:
We can use the four operations (addition, subtraction, multiplication and division) to solve real-world problems involving distances, intervals of time, volumes, masses of objects, and money. Include addition and subtraction problems involving simple fractions and problems that require expressing measurements given in a larger unit in terms of a smaller unit.