All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 9 Lesson 7 Subtract Mixed Numbers will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 4 Answer Key Chapter 9 Lesson 7 Subtract Mixed Numbers
You can use equivalent fractions to subtract mixed numbers.
Math in My World
Example 1
Olivia had 4\(\frac{3}{4}\) boxes of games. She gave 1\(\frac{1}{4}\) of the boxes to her brother. How many boxes of games does she have left?

Find 4\(\frac{3}{4}\) – 1\(\frac{1}{4}\).
1. Write each mixed number as an equivalent improper fraction.
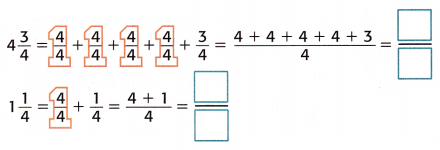
2. Subtract like fractions.
\(\frac{19}{4}\) – \(\frac{5}{4}\) = \(\frac{19-5}{4}\) = ![]()
3. Simplify. The models below show 14 divided into groups of 4.
\(\frac{14}{4}\) = 3\(\frac{2}{4}\) = 3 ![]()
So, Olivia has ______________ boxes of games left.
Check: Use addition to check.

3\(\frac{2}{4}\) + 1\(\frac{1}{4}\) = 1 + 1 + 1 + \(\frac{2}{4}\) + 1 + \(\frac{1}{4}\)
= 4\(\frac{3}{4}\)
Answer:
Number of boxes of games she have left = \(\frac{7}{2}\) or 3\(\frac{1}{2}\)
Explanation:
Number of boxes of games Olivia had = 4\(\frac{3}{4}\)
Number of boxes of games she gave to her brother = 1\(\frac{1}{4}\)
Number of boxes of games she have left = Number of boxes of games Olivia had – Number of boxes of games she gave to her brother
= 4\(\frac{3}{4}\) – 1\(\frac{1}{4}\)
= {[(4 × 4) + 3] ÷ 4} – {[(1 × 4) + 1] ÷ 4}
= [(16 + 3) ÷ 4] – [(4 + 1) ÷ 4]
= \(\frac{19}{8}\) – \(\frac{5}{4}\)
= [(19 – 5) ÷ 4]
= \(\frac{14}{4}\) ÷ \(\frac{2}{2}\)
= \(\frac{7}{2}\) or 3\(\frac{1}{2}\)
Check:
3\(\frac{2}{4}\) + 1\(\frac{1}{4}\) = 1 + 1 + 1 + \(\frac{2}{4}\) + 1 + \(\frac{1}{4}\)
= 4\(\frac{3}{4}\)

Example 2
Find 3\(\frac{1}{5}\) – 2\(\frac{2}{5}\).

1. Write each mixed number as an equivalent improper fraction.
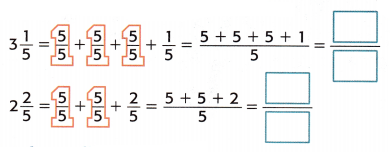
2. Subtract like fractions.
\(\frac{16}{5}\) – \(\frac{12}{5}\) = \(\frac{16-12}{5}\) = ![]() This fraction is already in simplest form.
This fraction is already in simplest form.
So, 3\(\frac{1}{5}\) – 2\(\frac{2}{5}\) = ![]() .
.
Check: Use addition to check.
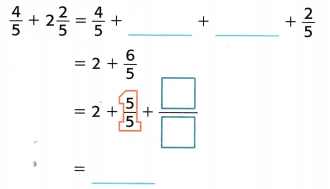
Answer:
Difference between 3\(\frac{1}{5}\) and 2\(\frac{2}{5}\), we get \(\frac{4}{5}\)
Explanation:
Subtraction between:
3\(\frac{1}{5}\) and 2\(\frac{2}{5}\)
= {[(3 × 5) + 1] ÷ 5} – {[(2 × 5) + 2] ÷ 5}
= [(15 + 1) ÷ 5] – [(10 + 2) ÷ 5]
= \(\frac{16}{5}\) – \(\frac{12}{5}\)
= [(16 – 12) ÷ 5]
= \(\frac{4}{5}\)
Check:
2\(\frac{2}{5}\) + \(\frac{4}{5}\)
= {[(2 × 5) + 2] ÷ 5} + \(\frac{4}{5}\)
= [(10 + 2) ÷ 5] + \(\frac{4}{5}\)
= \(\frac{12}{5}\) + \(\frac{4}{5}\)
= [(12 + 4) ÷ 5]
= \(\frac{16}{5}\) or 3\(\frac{1}{5}\)
Talk Math
Refer to the addition check in Example 2. What property allows you to group the whole numbers together and the like fractions together when adding?

Answer:
The commutative property allows you to group the whole numbers together and the like fractions together when adding.
Explanation:
The commutative property states that the order in which two numbers are added or multiplied does not affect the sum or product. For example: A fraction is a part of a whole. A fraction is written mathematically as one value on top of another, separated by a fraction bar.
Guided Practice
Find each difference. Write in simplest form.
Question 1.
5\(\frac{4}{8}\) – 1\(\frac{1}{8}\) = _________________
Answer:
Difference between 5\(\frac{4}{8}\) and 1\(\frac{1}{8}\), we get \(\frac{35}{8}\) or 4\(\frac{3}{8}\)
Explanation:
Subtraction between:
5\(\frac{4}{8}\) – 1\(\frac{1}{8}\)
= {[(5 × 8) + 4] ÷ 8} – {[(1 × 8) + 1] ÷ 8}
= [(40 + 4) ÷ 8] – [(8 + 1) ÷ 8]
= \(\frac{44}{8}\) – \(\frac{9}{8}\)
= [(44 – 9) ÷ 8]
= \(\frac{35}{8}\) or 4\(\frac{3}{8}\)
Question 2.
6\(\frac{1}{3}\) – 2\(\frac{2}{3}\) = _________________
Answer:
Difference between 6\(\frac{1}{3}\) and 2\(\frac{2}{3}\), we get \(\frac{11}{3}\) or 3\(\frac{2}{3}\)
Explanation:
Subtraction between:
6\(\frac{1}{3}\) – 2\(\frac{2}{3}\)
= {[(6 × 3) + 1] ÷ 3} – {[(2 × 3) + 2] ÷ 3}
= [(18 + 1) ÷ 3] – [(6 + 2) ÷ 3]
= \(\frac{19}{3}\) – \(\frac{8}{3}\)
= [(19 – 8) ÷ 3]
= \(\frac{11}{3}\) or 3\(\frac{2}{3}\)
Independent Practice
Find each difference. Write in simplest form. Use addition to check.
Question 3.
5\(\frac{4}{5}\) – 2\(\frac{2}{5}\) = _________________
Answer:
Difference between 5\(\frac{4}{5}\) and 2\(\frac{2}{5}\), we get \(\frac{17}{5}\) or 3\(\frac{2}{5}\)
Explanation:
Subtraction between:
5\(\frac{4}{5}\) – 2\(\frac{2}{5}\)
= {[(5 × 5) + 4] ÷ 5} – {[(2 × 5) + 2] ÷ 5}
= [(25 + 4) ÷ 5] – [(10 + 2) ÷ 5]
= \(\frac{29}{5}\) – \(\frac{12}{5}\)
= [(29 – 12) ÷ 5]
= \(\frac{17}{5}\) or 3\(\frac{2}{5}\)
Question 4.
3\(\frac{4}{6}\) – 1\(\frac{5}{6}\) = _________________
Answer:
Difference between 3\(\frac{4}{6}\) and 1\(\frac{5}{6}\), we get 2.
Explanation:
Subtraction between:
3\(\frac{4}{6}\) – 1\(\frac{5}{6}\)
= {[(3 × 6) + 4] ÷ 6} – {[(1 × 6) + 5] ÷ 6}
= [(18 + 4)÷ 5] – [(10 + 2) ÷ 5]
= \(\frac{22}{5}\) – \(\frac{12}{5}\)
= [(22 – 12) ÷ 5]
= \(\frac{10}{5}\) ÷ \(\frac{5}{5}\)
= \(\frac{2}{1}\)
= 2.
Question 5.
8\(\frac{2}{3}\) – 3\(\frac{2}{3}\) = __________________
Answer:
Difference between 8\(\frac{2}{3}\) and 3\(\frac{2}{3}\), we get 5.
Explanation:
Subtraction between:
8\(\frac{2}{3}\) – 3\(\frac{2}{3}\)
= {[(8 × 3) + 2] ÷ 3} – {[(3 × 3) + 2] ÷ 3}
= [(24 + 2)÷ 3] – [(9 + 2) ÷ 3]
= \(\frac{26}{3}\) – \(\frac{11}{3}\)
= [(26 – 11) ÷ 3]
= \(\frac{15}{3}\) ÷ \(\frac{3}{3}\)
= \(\frac{5}{1}\)
= 5.
Question 6.
6\(\frac{1}{4}\) – 4\(\frac{2}{4}\) = ___________________
Answer:
Difference between 6\(\frac{1}{4}\) and 4\(\frac{2}{4}\), we get \(\frac{7}{4}\) or 1\(\frac{3}{4}\)
Explanation:
Subtraction between:
6\(\frac{1}{4}\) – 4\(\frac{2}{4}\)
= {[(6 × 4) + 1] ÷ 4} – {[(4 × 4) + 2] ÷ 4}
= [(24 + 1)÷ 4] – [(16 + 2) ÷ 4]
= \(\frac{25}{4}\) – \(\frac{18}{4}\)
= [(25 – 18) ÷ 4]
= \(\frac{7}{4}\) or 1\(\frac{3}{4}\)
Question 7.
4\(\frac{2}{3}\) – 2\(\frac{1}{3}\) = ___________________
Answer:
Difference between 4\(\frac{2}{3}\) and 2\(\frac{1}{3}\), we get \(\frac{7}{3}\) or 1\(\frac{4}{3}\)
Explanation:
Subtraction between:
4\(\frac{2}{3}\) – 2\(\frac{1}{3}\)
= {[(4 × 3) + 2] ÷ 3} – {[(2 × 3) + 1] ÷ 3}
= [(12 + 2)÷ 3] – [(6 + 1) ÷ 3]
= \(\frac{14}{3}\) – \(\frac{7}{3}\)
= [(14 – 7) ÷ 3]
= \(\frac{7}{3}\) or 1\(\frac{4}{3}\)
Question 8.
6\(\frac{3}{4}\) – 3\(\frac{2}{4}\) = ___________________
Answer:
Difference between 6\(\frac{3}{4}\) and 3\(\frac{2}{4}\), we get \(\frac{13}{3}\) or 4\(\frac{1}{3}\)
Explanation:
Subtraction between:
6\(\frac{3}{4}\) – 3\(\frac{2}{4}\)
= {[(6 × 4) + 3] ÷ 4} – {[(3 × 4) + 2] ÷ 4}
= [(24 + 3)÷ 4] – [(12 + 2) ÷ 4]
= \(\frac{27}{4}\) – \(\frac{14}{4}\)
= [(27 – 14) ÷ 3]
= \(\frac{13}{3}\) or 4\(\frac{1}{3}\)
Question 9.
9\(\frac{5}{6}\) – 7\(\frac{2}{6}\) = __________________
Answer:
Difference between 9\(\frac{5}{6}\) and 7\(\frac{2}{6}\), we get 5.
Explanation:
Subtraction between:
9\(\frac{5}{6}\) – 7\(\frac{2}{6}\)
= {[(9 × 6) + 5] ÷ 6} – {[(7 × 6) + 2] ÷ 6}
= [(54 + 5)÷ 6] – [(42 + 2) ÷ 6]
= \(\frac{59}{6}\) – \(\frac{44}{6}\)
= [(59 – 44) ÷ 3]
= \(\frac{15}{3}\) ÷ \(\frac{3}{3}\)
= \(\frac{5}{1}\)
= 5.
Question 10.
6\(\frac{7}{8}\) – 1\(\frac{5}{8}\) = ___________________
Answer:
Difference between 6\(\frac{7}{8}\) and 1\(\frac{5}{8}\), we get 14.
Explanation:
Subtraction between:
6\(\frac{7}{8}\) – 1\(\frac{5}{8}\)
= {[(6 × 8) + 7] ÷ 8} – {[(1 × 8) + 5] ÷ 8}
= [(48 + 7)÷ 8] – [(8 + 5) ÷ 8]
= \(\frac{55}{8}\) – \(\frac{13}{8}\)
= [(55 – 13) ÷ 3]
= \(\frac{42}{3}\) ÷ \(\frac{3}{3}\)
= \(\frac{14}{1}\)
= 14.
Question 11.
4\(\frac{6}{12}\) – 3\(\frac{5}{12}\) = ___________________
Answer:
Difference between 4\(\frac{6}{12}\) and 3\(\frac{5}{12}\), we get \(\frac{13}{3}\) or 4\(\frac{1}{3}\)
Explanation:
Subtraction between:
4\(\frac{6}{12}\) – 3\(\frac{5}{12}\)
= {[(4 × 12) + 6] ÷ 12} – {[(3 × 12) + 5] ÷ 12}
= [(48 + 6)÷ 12] – [(36 + 5) ÷ 12]
= \(\frac{54}{12}\) – \(\frac{41}{12}\)
= [(54 – 41) ÷ 12]
= \(\frac{13}{3}\) or 4\(\frac{1}{3}\)
Problem Solving
Question 12.
Mathematical PRACTICE Identify Structure Mrs. Garcia has 5\(\frac{6}{8}\) boxes of paper. She uses 3\(\frac{7}{8}\) boxes. How many boxes does she have left? Write in simplest form.
Answer:
Number of boxes of paper she have left = \(\frac{15}{8}\) or 1\(\frac{7}{8}\)
Explanation:
Number of boxes of paper Mrs. Garcia has = 5\(\frac{6}{8}\)
Number of boxes of paper she uses = 3\(\frac{7}{8}\)
Number of boxes of paper she have left = Number of boxes of paper Mrs. Garcia has – Number of boxes of paper she uses
= 5\(\frac{6}{8}\) – 3\(\frac{7}{8}\)
= {[(5 × 8) + 6] ÷ 8} – {[(3 × 8) + 7] ÷ 8}
= [(40 + 6)÷ 8] – [(24 + 7) ÷ 8]
= \(\frac{46}{8}\) – \(\frac{31}{8}\)
= [(46 – 31) ÷ 8]
= \(\frac{15}{8}\) or 1\(\frac{7}{8}\)
Question 13.
Erwin had 2\(\frac{5}{12}\) gallons of lemonade. He spilled \(\frac{11}{12}\) gallon of lemonade. How much lemonade does he have left? Write in simplest form.
Answer:
Number of gallons of lemonade he have left = \(\frac{3}{2}\) or 1\(\frac{1}{2}\)
Explanation:
Number of gallons of lemonade Erwin had = 2\(\frac{5}{12}\)
Number of gallons of lemonade he spilled = \(\frac{11}{12}\)
Number of gallons of lemonade he have left = Number of gallons of lemonade Erwin had – Number of gallons of lemonade he spilled
= 2\(\frac{5}{12}\) – \(\frac{11}{12}\)
= {[(2 × 12) + 5] ÷ 12} – \(\frac{11}{12}\)
= [(24 + 5) ÷ 12] – \(\frac{11}{12}\)
= \(\frac{29}{12}\) – \(\frac{11}{12}\)
= [(29 – 11) ÷ 12]
= \(\frac{18}{12}\) ÷ \(\frac{6}{6}\)
= \(\frac{3}{2}\) or 1\(\frac{1}{2}\)
Question 14.
Mathematical PRACTICE Identify Structure Abby had 4\(\frac{7}{10}\) boxes of crackers. She used 1\(\frac{3}{10}\) boxes of crackers to make a snack for her class. How many boxes of crackers does she have left? Write in simplest form.
Answer:
Number of boxes of crackers she have left = \(\frac{7}{5}\) or 1\(\frac{2}{5}\)
Explanation:
Number of boxes of crackers Abby had = 4\(\frac{7}{10}\)
Number of boxes of crackers to make a snack for her class she used = 1\(\frac{3}{10}\)
Number of boxes of crackers she have left = Number of boxes of crackers Abby had – Number of boxes of crackers to make a snack for her class she used
= 4\(\frac{7}{10}\) – 1\(\frac{3}{10}\)
= {[(4 × 10) + 7] ÷ 10} – {[(1 × 10) + 3] ÷ 10}
= [(40 + 7) ÷ 10] – [(30 + 3) ÷ 10]
= \(\frac{47}{10}\) – \(\frac{33}{10}\)
= [(47 – 33) ÷ 10]
= \(\frac{14}{10}\) ÷ \(\frac{2}{2}\)
= \(\frac{7}{5}\) or 1\(\frac{2}{5}\)
HOT Problems
Question 15.
Mathematical PRACTICE Keep Trying Find the missing mixed number.
_______________ – 2\(\frac{1}{3}\) = 3\(\frac{1}{3}\)
Answer:
Missing mixed number in this equation:
8\(\frac{1}{3}\) – 2\(\frac{1}{3}\) = 3\(\frac{1}{3}\)
Explanation:
Equation given:
?? – 2\(\frac{1}{3}\) = 3\(\frac{1}{3}\)
=> ?? = 3\(\frac{1}{3}\) + 2\(\frac{1}{3}\)
=> ?? = {[(3 × 3) + 1] ÷ 3} + {[(2 × 3) + 1] ÷ 3}
=> ?? = [(9 + 1) ÷ 3] + [(6 + 1) ÷ 3]
=> ?? = \(\frac{10}{3}\) + \(\frac{7}{3}\)
=> ?? = [(10 + 7) ÷ 3]
=> ?? = \(\frac{17}{3}\) or 8\(\frac{1}{3}\)
=> Missing mixed number = 8\(\frac{1}{3}\)
Question 16.
Building on the Essential Question Why should I use addition to check the answer to a subtraction problem?
Answer:
To check the answer we can add the difference to the smaller number and if the sum equals to the larger number, our answer is correct, we use addition to check the answer to a subtraction problem.
Explanation:
We can use addition to check subtraction because we have learnt that we subtract smaller number from the larger number to find the difference of two numbers. Therefore, to check the answer we can add the difference to the smaller number and if the sum equals to the larger number, our answer is correct.