We included HMH Into Math Grade 8 Answer Key PDF Module 5 Lesson 4 Compare Proportional Relationships to make students experts in learning maths.
HMH Into Math Grade 8 Module 5 Lesson 4 Answer Key Compare Proportional Relationships
I Can identify and compare proportional relationships presented in different ways.
Step It Out
1. Three friends, Brooklyn, Lincoln, and Taylor, competed in a race over the weekend. Which runner ran the fastest?
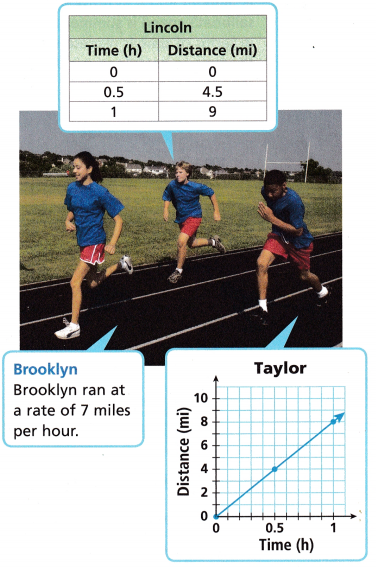
A. Choose a point in the table and use it to calculate the pace, in miles per hour, at which Lincoln ran.
_________________________
_________________________
Answer:
From the table, we can see that,
Lincoln ran 4.5 miles in 30 minutes.
1 hour = 60 min
60 min = 4.5 × 2 = 9 miles
Thus Lincoln ran 9 miles per hour.
B. Taylor’s pace is the same as the unit rate, which can be calculated by dividing the y-coordinate by the x-coordinate. Find a point on the graph and use it to calculate the pace, in miles per hour, at which Taylor ran.
_________________________
_________________________
Answer:
Taylor ran 4 miles in 30 min or 0.5 hr.
1 hour = 4 × 2 = 8 miles
Thus Taylor ran 8 miles per hour.
C. The unit rates you found can now be compared to the rate at which Brooklyn ran. Which runner ran the fastest? Complete the following sentences.
Brooklyn ran at a rate of ___ miles per hour.
____ ran the fastest because his/her rate is the fastest at _____ miles per hour.
Answer:
Brooklyn ran at a rate of 7 miles per hour.
Lincoln ran 9 miles per hour.
Lincoln ran the fastest because his/her rate is the fastest at 9 miles per hour.
Turn and Talk If you were going to present each runner’s rate in the same way for 3 hours, which representation—graph, table, or verbal description—would you choose? Why?
2. A sailboat and a motorboat each are traveling at a constant rate. The sailboat’s speed is summarized in the graph. The motorboat’s distance in terms of time is represented by the equation y = 60x, where x is the time in hours and y is the distance traveled in miles. Compare the speeds of the two boats.
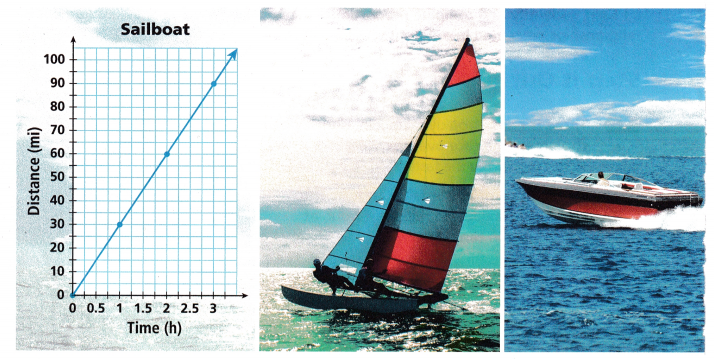
A. Determine the unit rate for the sailboat.
After traveling 1 hour, the sailboat has gone ____ miles, so the unit rate of the sailboat is miles per hour.
Answer:
From the above graph we can see that, After traveling 1 hour, the sailboat has gone 30 miles, so the unit rate of the sailboat is miles per hour.
B. Determine the unit rate for the motorboat. Substitute 1 hour into the equation y = 60x and solve for the distance traveled.
y = 60(______)
y = ______
The unit rate of the motorboat ______ is miles per hour.
Answer:
Substitute 1 hour into the equation y = 60x and solve for the distance traveled.
y = 60(1)
y = 60
The unit rate of the motorboat 60 miles per hour.
C. Which boat traveled faster? How do you know?
____________________
Answer:
Motorboats traveled faster than sailboats.
The unit rate of the motorboat 60 miles per hour.
sailboat has gone 30 miles per hour.
60 – 30 = 30 miles
D. If you were to graph the motorboat’s progress on the same axes as the sailboat’s progress, would the motorboat’s line be steeper or less steep than the sailboat’s line? Why?
____________________
Turn and Talk How would you need to change the graph if you wanted to represent the progress of both boats over 3 hours on the same graph?
3. A grocery store and a street vendor are each selling bananas by the pound. You can buy 2 pounds of bananas from a Street vendor for $1.62. The cost of bananas at a grocery store is shown in the photo.
A. Complete the table.

B. Find the cost of a pound of bananas from the Street vendor.
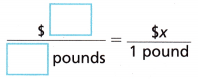
The unit rate is $____ per pound.
C. Five pounds of bananas cost 5($ ![]() ), or $
), or $ ![]() .
.
D. The (grocery store / street vendor) is selling bananas at the lower price.
if you purchase 5 pounds of bananas, you save ____ purchasing bananas for the lower price.
Answer:
1 pound = $0.79
2 pound = 2 × $0.79 = $1.58
3 lb = 3 × 0.79 = $2.37
5 lb = 5 × 0.79 = $3.95
8 lb = 8 × 0.79 = $6.32

B. A grocery store and a street vendor are each selling bananas by the pound. You can buy 2 pounds of bananas from a Street vendor for $1.62.
2 pounds = $1.62
1 pound = 1.62/2 = $0.81
The unit rate is $0.81 per pound.
C. Five pounds of bananas cost 5 × 0.81 = $4.05
D. The street vendor is selling bananas at a lower price.
4.05 – 3.95 = $0.10
If you purchase 5 pounds of bananas, you save $0.10 purchasing bananas for the lower price.
Check Understanding
Use the information to answer Problems 1-2.
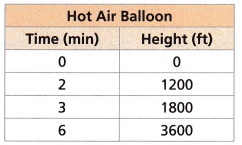
The height of a hot air balloon over time is given in the following table.
The height of a blimp over time is given by y = 250x, where y represents the height in feet and x represents the time in minutes.
Question 1.
How fast is the hot air balloon rising? How fast is the blimp rising?

Answer:
1200 ft in 2 mins
1 min = 1200/2 = 600 ft
Thus the hot air balloon rising 600 ft per min.
blimp rising:
y = 250x
y = 250(1)
y = 250 ft
1 min = 250 ft
Thus blimp rising 250 ft per min.
Question 2.
Is the hot air balloon or the blimp rising faster? By how much?
Answer:
Blimp rising 250 ft per min.
Hot air balloon rising 600 ft per min.
600 – 250 = 350ft
Thus hot air balloon is rising faster than a blimp rising.
On Your Own
Use the information to answer Problems 3-8.
A researcher recorded facts about the flight of a duck, a crow, and a seagull. The duck’s rate of flight was 20 miles per hour.

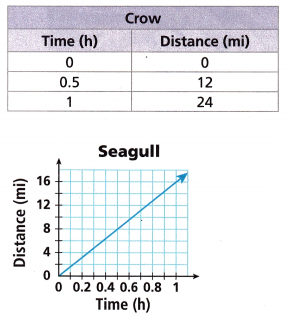
Question 3.
Did the crow fly at a constant rate? How do you know?
_________________
Answer:
0.5 hr = 12 miles
1 hr = 12 × 2 = 24 miles
Yes, the crow fly at a constant rate.
Question 4.
Did the seagull fly at a constant rate? How do you know?
_________________
Answer:
1 hour = 16 miles
0.4 hour = 8 miles
No, the seagull fly at a constant rate.
Question 5.
How fast did the crow fly? How fast did the seagull fly?
_________________
Answer:
Crow fly 24 miles per hour.
seagull fly 16 miles per hour.
Question 6.
A. Complete the following sentences.
The duck flew at a rate of ___ miles per hour.
Did the seagull or the duck fly at a faster rate? _____
Did the crow or the duck fly at a faster rate? ______
Answer:
The duck flew at a rate of 20 miles per hour.
Seagull fly 16 miles per hour.
Crow fly 24 miles per hour.
B. The ____ flew the fastest.
Answer: The crow flew the fastest.
Question 7.
After 5 hours of flight, how much farther would the fastest bird have traveled than the slowest bird?
Answer:
Crow fly 24 miles per hour.
5 hours = 24 × 5 = 120 miles
Seagull fly 16 miles per hour.
5 hours = 16 × 5 = 80 miles
120 – 80 = 40 miles
After 5 hours of flight, a crow flies faster than a seagull.
Question 8.
What does (0, 0) represent for each of the birds?
_________________________
Answer: (0, 0) represent at 0 hour the bird fly 0 mile.
Question 9.
Reason A rain barrel and a cistern are filling at constant rates. The amount of water in the rain barrel over time is shown in the graph. The amount of water in the cistern is given by y = 200x, where x is the time in hours and y is gallons of water.

A. How fast is the rain barrel filling? How fast is the cistern filling?
____________________
Answer:
From the graph,
Rain barrel filling is 75 gallon per hour
The amount of water in the cistern is given by y = 200x, where x is the time in hours and y is gallons of water.
y = 200(1)
y = 200
200 gallon per hour.
B. If both the barrel and the cistern were empty at t = 0, which would completely fill first? Explain.
____________________
Answer:
If both the barrel and the cistern were empty at t = 0
The cistern would fill first than rain barrel.
Question 10.
A video downloads at a constant rate given by y = 5x, where y represents the percent of the file downloaded and x represents the time in seconds. A game’s download progress is shown in the table.
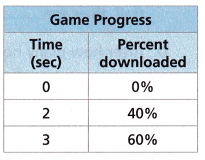
A. At what rate is the game downloading? How long does it take to download the game?
Answer:
At t = 0 the percent downloaded is 0
At t = 2 the percent downloaded is 40%
At t = 1 the percent downloaded is 40/2 = 20%
20% downloaded per second.
B. At what rate is the video downloading? How long does it take to download the video?
Answer:
At t = 0
Video downloads at a constant rate given by y = 5x, where y represents the percent of the file downloaded and x represent the time in seconds.
y = 5(0)
y = 0
At t = 2
y = 5(2)
y = 10%
At t = 3
y = 5(3)
y = 15%
At t = 1
10/2 = 5%
5% downloaded per second.
C. The size of a digital file can be measured in megabytes (“MB”). If the video is 200 MB and the game is 100 MB, what are the download speeds of the two files?
Answer:
The download speed of game downloading is faster than video downloading.
Question 11.
The graph shows Peg’s progress on a walking trail, showing the distance from the start of the trail she has walked over time. Her friend Raj travels along the same walking trail.

A. How fast is Peg walking?
_________________
Answer:
At t = 2 hour
peg walk a distance of 6 miles.
At t = 1 hour
Peg walk distance of 6/2 = 3 mile per hour.
B. Use Structure Complete the table.

C. If Peg and Raj started at the same time from the same place on the trail, they are ___ miles apart after 3 hours.
D. After how many hours will Peg and Raj be 2 miles apart?
________________________
Answer:
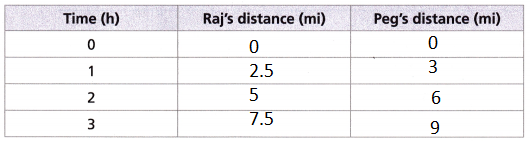
If Peg and Raj started at the same time from the same place on the trail, they are 1.5 miles apart after 3 hours.
After 1 hour Peg and Raj be 2 miles apart.
Question 12.
Financial Literacy Romeo is buying granola. He can either buy it in bulk for $4.50 per pound, or he can buy a box that contains 1.25 pounds of granola for $6.
A. What is the cost per pound for each granola option?
____________________
____________________
Answer:
Given,
Romeo is buying granola. He can either buy it in bulk for $4.50 per pound, or he can buy a box that contains 1.25 pounds of granola for $6.
4.5 per pound
6 ÷ 1.25 = $4.8 per pound
B. How much does he save buying 2.5 pounds in bulk?
____________________
Answer: 2.5 × (4.8 – 4.5)
2.5 × 0.3 = $0.75
C. How many pounds would he have to buy in order to save $3.00?
____________________
Answer:
3 ÷ (4.8 – 4.5)
3 ÷ (0.3) = 10 pounds
Lesson 5.4 More Practice/Homework
Question 1.
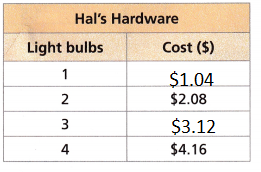
Financial Literacy Hal’s Hardware and Sal’s Supermarket are both selling light bulbs.
A. Use Structure Complete the table.
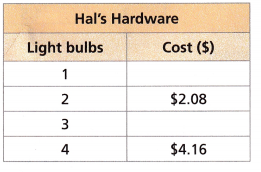
Answer:
2 bulbs = $2.08
1 bulb = x
2x = $2.08
x = 2.08/2
x = $1.04
3 bulbs = 3 × 1.04 = $3.12

B. Calculate the unit price of light bulbs at Sal’s Supermarket.
_______________________
Answer:
Cost of 3 lightbulbs = $4.26
1 lightbulb = 4.26/3 = $1.42
Thus the unit price of light bulbs at Sal’s Supermarket is $1.42
C. What is the cost of 6 light bulbs at each store?
_______________________
Answer:
The unit price of light bulbs at Sal’s Supermarket is $1.42
Cost of 6 light bulbs = 6 × 1.42 = $8.52
Cost of 1 lightbulb at Hal’s hardware is $1.04
Cost of 6 light bulbs = 1.04 × 6 = $6.24
D. Compare the cost of 9 light bulbs from Sal’s Supermarket to the cost of 9 light bulbs at Hal’s Hardware. Which store is selling light bulbs at a lower unit price? How much less does it cost to purchase 9 light bulbs from that store?
_______________________
Answer:
Cost of 1 lightbulb at Hal’s hardware is $1.04
cost of 9 light bulbs at Hal’s Hardware = 9 × 1.04 = $9.36
cost of 9 light bulbs from Sal’s Supermarket = 9 × 1.42 = $12.78
12.78 – 9.36 = $3.42
Hal’s Hardware is selling at a lower unit price of less than $3.42
Question 2.
A coffee maker and a juice maker are making beverages. The rate at which the coffee is being made is given by y = 6x, where y represents the amount of coffee in mL and x represents the time passed in seconds. The amount of juice that has been made at different times is summarized in the table.
A. At what rate is the coffee maker making coffee?
____________________
Answer:
The rate at which the coffee is being made is given by y = 6x
y = 6(1)
y = 6
So, the rate is 6 ml/sec.
B. At what rate ¡s the juice maker making juice?
_________________
Answer:
y = 8x
y = 8(1)
y = 8
So, the rate of making juice is 8mL/sec.
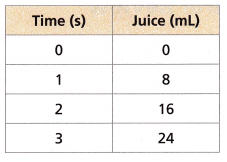
C. Is juice or coffee being made at a faster rate?
_________________
Answer: Juice is being made at a faster rate than coffee.
Test Prep
Question 3.
A spider is crawling at a constant rate of 0.4 centimeters per second. The distance that a ladybug has walked over time is summarized in the table.The (spider /ladybug) is traveling at a faster rate.
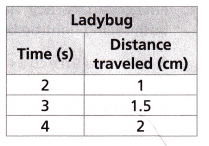
Answer:
Given,
A spider is crawling at a constant rate of 0.4 centimeters per second.
The distance that a ladybug has walked over time is summarized in the table.
2 sec = 1 cm
1 sec = 0.5 cm
The spider is traveling at a faster rate than the ladybug.
Question 4.
The rate at which a mountain is eroding is given by y = 0.5x, where y represents the amount of erosion in millimeters and x represents the amount of time in years. A field is eroding at a rate of 2 millimeters per year. Is the field or the mountain eroding at a faster rate? By how much?
Answer:
Given,
The rate at which a mountain is eroding is given by y = 0.5x,
where y represents the amount of erosion in millimeters and x represents the amount of time in years.
A field is eroding at a rate of 2 millimeters per year.
dy/dx = 0.5 mm/year
2 > 0.5
Thus the field is eroding at a faster rate.
2 – 0.5 = 1.5 mm/year
Question 5.
A baker is baking muffins and a loaf of fruit bread. The bread is rising at a rate of 0.03 inch per minute. The amount that the muffins have risen from their initial size at different points of baking time is given on the graph.
The (loaf of bread / muffins) rise(s) at a faster rate.
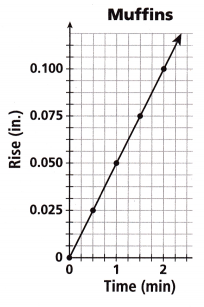
Answer:
A baker is baking muffins and a loaf of fruit bread.
The bread is rising at a rate of 0.03 inch per minute.
From the above graph we can see that Muffins is rising at a rate of 0.050 inch per minute.
Thus the loaf of Muffins rises at a faster rate.
Question 6.
The unit rate of the proportional relationship y = 2x is ___
A. y
B. \(\frac{2}{1}\)
C. x
D. \(\frac{1}{2}\)
Answer:
The unit rate of the proportional relationship y = 2x
y = kx
k = 2
Option B is the answer.
Question 7.
A bumblebee visits 14 flowers in 38 minutes to collect pollen. A butterfly’s progress in visiting flowers is shown in the table. Which insect is visiting flowers at a faster rate? _____
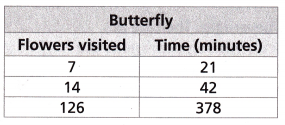
Answer:
Given,
A bumblebee visits 14 flowers in 38 minutes to collect pollen.
Rate of bumblebee = 38/14 = 19/7 = 1 5/7 flowers/min
Rate of butterfly = 21/7 = 3 flowers/min
Thus the butterfly is visiting the flowers at a faster rate.
Spiral Review
Question 8.
Is the graph of the distance a person has driven over time an example of a continuous or discrete graph?
_________________
Answer:
The distance a person has driven over time is a continuous graph.
Question 9.
Solve 3x – 1 = 5.
_________________
Answer:
3x – 1 = 5
3x = 5 + 1
3x = 6
x = 2
Question 10.
Solve 4(2 + x) = 6 + 6x.
_________________
Answer:
4(2 + x) = 6 + 6x
8 + 4x = 6 + 6x
4x – 6x = 6 – 8
-2x = -2
x = 1