We included HMH Into Math Grade 8 Answer Key PDF Module 12 Lesson 2 Understand Scientific Notation to make students experts in learning maths.
HMH Into Math Grade 8 Module 12 Lesson 2 Answer Key Understand Scientific Notation
I Can use scientific notation to describe very large or very small quantities and to compare quantities.
Step It Out
Question 1.
What does one trillion dollars look like? If you could stack one trillion one-dollar bills, the stack would be about 68,000 miles tall. This is more than one-fourth the distance from the Earth to the moon!
The standard, or decimal, form of a number is one way to write numbers. It uses the base-ten system to show all of a number’s digits. For example, the way to write one trillion in standard form is 1,000,000,000,000.
There is a shorthand way, called scientific notation, to write large numbers without so many zeros. 1,000,000,000,000 in scientific notation is 1 ื 1012.
A. To write 68,000 miles in scientific notation, first move the decimal point to the left to get a number that is greater than or equal to 1 but less than 10.
Connect to Vocabulary
Scientific notation is a method of writing very large or very small numbers by using powers of 10. In scientific notation, a number is written as the product of two factors. The first factor is greater than or equal to 1 but less than 10, and the second factor is a power of 10.
The decimal point moves ___________ places to the left.
Remove the extra zeros to get the first factor for scientific notation: __________.
Answer:
68,000 in scientific notation is 6.8 x 104
The decimal point moves 4 places to the left.
Remove the extra zeros to get the first factor for scientific notation is6.8 x 104.
B. Use this factor and a power of 10 to write the number in scientific notation.
68,000 = _________ × 
When you write a number in scientific notation, its value does not change.
Answer:
68,000 in scientific notation is 6.8 x 104
When you write a number in scientific notation, its value does not change.
C. Write one billion, 1,000,000,000, in scientific notation.
1,000,000,000 = ___________ ×
Answer:
Given that,
1,000,000,000, in scientific notation is 109
The decimal point moves 9 places to the left.
Turn and Talk Is the number 16 × 107 written in scientific notation Why or why not?
Answer:
Question 2.
You can also use scientific notation for very small numbers. The thickness of a dollar bill is about 0.0043 inches. Write this quantity in scientific notation.
A. First move the decimal point to the right to get a number that is greater than or equal to 1 but less than 10.
0. 0 0 4 3 The decimal point moves ___________ places to the right.
Remove the extra zeros to get the first factor: ____________.
Answer:
First, move the decimal point to the right to get a number that is greater than or equal to 1 but less than 10.
0. 0 0 4 3 The decimal point moves 3 places to the right.
Remove the extra zeros to get the first factor is 4.3.
B. Since 0.0043 is less than 1, you moved the decimal point to the right, so the exponent in the power of 10 will be negative.
0.0043 = _________ ×
Answer:
0.0043 in scientific notation is 4.3 x 103
Here the decimal point moves 3 places to the right.
Question 3.
In 2016, the United States Mint produced about 9.1 × 109 pennies. Write this quantity in standard form.
A. Use the power of 10 to determine how many places you will need to move the decimal point.
Move the decimal point __________ places.
Answer:
The United States Mint produced about 9.1 × 109 pennies.
9.1 × 109 in standard form is 9,100,000,000
Move the decimal point right to 9 places.
B. Write the number with placeholder zeros. Then move the decimal point to the right the appropriate number of places.
9.1 0 0 0 0 0 0 0 0 So, 9.1 × 109 = ______________
Answer:
The number with place holders is 9.1 0 0 0 0 0 0 0 0.
Then move the decimal point to the right the 9 number of places.
Question 4.
Scientific notation makes it easy to compare quantities.
A. The table shows the number of half-dollar coins produced in 2016. Use a ratio to compare these quantities.
\(\frac{4.2 \times 10^{6}}{2.1 \times 10^{6}}\)
The powers of 10 are the same: = \(\frac{10^{6}}{10^{6}}\) or 100 or ________.
Compare the first factors: 
= ___________.
So, the total number of half-dollar coins minted is about 
• = ___________ times the number of half-dollar coins minted in Denver.
Answer:
Given that,
\(\frac{4.2 \times 10^{6}}{2.1 \times 10^{6}}\)
The powers of 10 are the same: = \(\frac{10^{6}}{10^{6}}\) or 100 or 1
Compare the first factors: 4.2/2.1= 2.
So, the total number of half-dollar coins minted is about 2 x 1= 3 times the number of half-dollar coins minted in Denver.
Turn and Talk Why is scientific notation a good way to express very large or very small numbers that you are estimating?
Answer:
B. Use the ratio \(\frac{3.45 \times 10^{-8}}{3.45 \times 10^{-11}}\) to compare 3.45 × 10-8 and 3.45 × 10-11.
First compare the powers of 10.
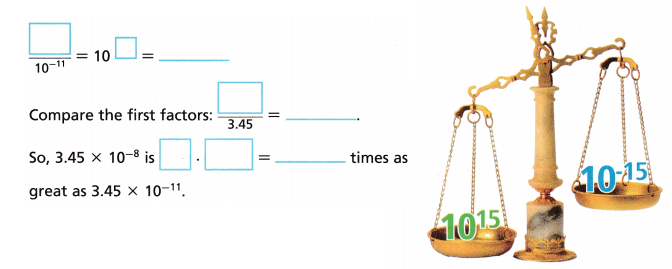
Answer:
10-8/10-11 = 103 = 1000.
Compare the first factors 3.45/3.45 = 1.
So, 3.45 × 10-8 is 1 x 103 = 1000 times as great has 3.45 × 10-11
C. Use a ratio to compare 4.8 × 109 and 12,000,000.
Write 12,000,000 in scientific notation. 12,000,000 = _____________
Compare the powers of 10. Compare the greater power to the lesser power.
= ____________
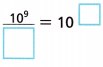Compare the first factors: 
= ____________
So, 4.8 × 109 is _______ × __________ = ___________ times as great as 12,000,000.
Answer:
Write 12,000,000 in scientific notation. 12,000,000 = 1.2 x 107
Compare the powers of 10. Compare the greater power to the lesser power.
109/107 = 102
Compare the first factors: 4.8/1.2 = 4
So, 4.8 × 109 is 4 × 102 = 400 times as great as 12,000,000.
D. Use a ratio to compare 0.00222 and 66,600.
In scientific notation, 0.00222 = __________
In scientific notation, 66,600 = __________
66,600 is __________ × __________ = __________ times as great as 0.00222.
Answer:
Given that,
In scientific notation, 0.00222 = 2.22 x 10-4
In scientific notation, 66,600 = 6.66 x 103
10-4/103 = 10-2
6.66/2.22 = 3
66,600 is 3 x 10-1 = 0.3 times as great as 0.00222.
Check Understanding
Question 1.
Which number is greater: 8.9 × 105 or 2.1 × 107? How can you tell without writing the numbers in standard notation?
Answer:
Given that the numbers are
8.9 × 105
2.1 × 107
we can write 8.9 × 105 = 0.087 x 107
2.1 × 107 greater than 8.9 × 105
Question 2.
Write 0.000501 in scientific notation.
Answer:
0.000501 in scientific notation is 5.01 x 10-4
Move the decimal 4 times to the left then it is 5.01. But the 5.01 is less than 10.
Moved the decimal to the left is the exponent and the exponent is negative.
Question 3.
Write 5.31 × 103 in standard form.
Answer:
Given that
5.31 × 103 in standard form is
103 = 1000
Multiply 5.31 x 1000 = 5,310.
On Your Own
Question 4.
The photo shows a road sign in western Australia.
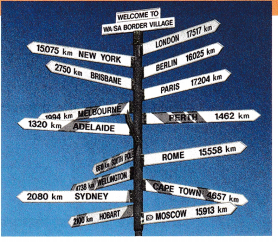
A. Write the distance to Rome in scientific notation.
Answer:
The distance to the Rome is 15558 km
15,558 in scientific notation is 1.5558 x 104
Move the decimal 4 times to the left then it is 1.5558. But the 1.5558 is less than 10.
Moved the decimal to the left is the exponent and the exponent is positive.
B. Write the distance to Sydney in scientific notation.
Answer:
The distance to the Rome is 2080 km
2080 in scientific notation is 2.080 x 103
Move the decimal 3 times to the left then it is 2.080. But the 2.080 is less than 10.
Moved the decimal to the left is the exponent and the exponent is positive.
C. Reason Explain how you can use the scientific notation version of the distances to determine whether it is farther to Rome or to Sydney.
Answer:
The distance to the Rome is 15558 km
15,558 in scientific notation is 1.5558 x 104
The distance to the Rome is 2080 km
2080 in scientific notation is 2.080 x 103
The distance to Rome is faster.
Question 5.
STEM The diameter of a carbon atom is approximately 0.000000017 centimeter.
A. When the diameter is expressed in scientific notation, will the exponent be positive or negative? How do you know?
Answer:
0.000000017 centimeters in the scientific notation is 1.7 x 10-8
The exponent is negative.
B. Write the diameter in scientific notation. Show your work and explain your steps.
Answer:
0.000000017 centimeters in the scientific notation is 1.7 x 10-8
Move the decimal 8 times to the right then it is 1.7. But the 1.7 is less than 10.
Moved the decimal to the right is the exponent and the exponent is negative.
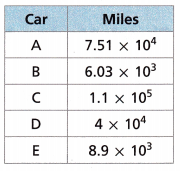
For Problems 6-7, use the table which shows the number of miles on the odometers of several cars.
Question 6.
Write the number of miles on Car A’s odometer in standard form.
Answer:
Given that,
The number of miles on Car A’s odometer = 7.51 x 104
104 = 10,000
7.51 x 10,000 = 75,100
7.51 x 104 in the standard form is 75,100.
Question 7.
Attend to Precision Nicole wants to buy a used car with fewer than 50,000 miles on the odometer. Which of the cars shown should Nicole consider? Explain.
Answer:
7.51 x 104 in the standard form is 75,100
6.03 x 103 in the standard form is 6,030
1.1 x 105 in the standard form is 110,000
4 x 104 in the standard form is 40,000
8.9 x 103 in the standard form is 8,900
A car with fewer than 50,000 miles on the odometer is B, D, E.
The car holder Nicole considers the B, D, and E cars.
For Problems 8-9, use the table of bridge lengths shown.
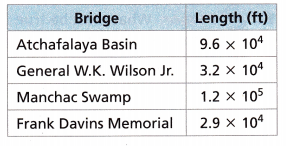
Question 8.
Which of the bridges shown is the longest? How do you know?
Answer:
Atchafalaya Basin’s bridge length is 9.6 x 104 = 96,000
General W.K. Wilson Jr’s bridge length is 3.2 x 104 = 32,000
Manchac Swamp bride length is 1.2 x 105 = 120,000
Frank Davins Memorial bridge length is 2.9 x 104 = 29,000.
The largest bridge is the Manchac Swamp bride.
Question 9.
How many times as long as General W.K. Wilson Jr. Bridge is Atchafalaya Basin Bridge? Explain.
Answer:
General W.K. Wilson Jr’s bridge length is 3.2 x 104 = 32,000
Atchafalaya Basin’s bridge length is 9.6 x 104 = 96,000
Therefore 96,000/32,000 = 3
General W.K. Wilson Jr. Bridge is 3 times long as Atchafalaya Basin Bridge.
Question 10.
STEM A geologist is comparing two rock samples. Sample A has a mass of 0.0015 gram. Sample B has the mass shown on the scale.
A. Write the masses in scientific notation.
Answer:
Sample A has a mass of 0.0015 grams.
Sample B has a mass of 750.0 grams.
Sample B is greater than Sample A.
B. How many times as great as the mass of Sample A is the mass of Sample B? Show your work.
Answer:
Given that,
Sample A has a mass of 0.0015 grams.
Sample B has a mass of 750.0 grams.
Therefore 750.0/0.0015 = 500,000
Sample A is 500,000 times greater than Sample B.
Question 11.
Use Tools Most calculators display scientific notation when a result is longer than the number of digits the screen can display.
A. To find out how your calculator displays scientific notation, enter 240 and press the ENTER key. What does the calculator display? What number in scientific notation does it represent?
Answer:
B. Write the value of 240 rounded to the nearest trillion.
Answer:
Question 12.
Reason What must be true about the exponent when you write a whole number between 1 and 10 in scientific notation? Why? Give an example.
Answer:
For Problems 13-16, write each number in scientific notation.
Question 13.
47,100,000
Answer:
Given that the number is 47,100,000.
47,100,000 in scientific notation is 4.71 x 107
Move the decimal 7 times to the left then it is 4.71. But the 4.71 is less than 10.
Moved the decimal to the left is the exponent and the exponent is positive.
Question 14.
6004
Answer:
Given that,
6004 in scientific notation is 6.004 x 103
Move the decimal 3 times to the left then it is 6.004. But the 6.004 is less than 10.
Moved the decimal to the left is the exponent and the exponent is positive.
Question 15.
0.0000000009
Answer:
Given that,
0.0000000009 in scientific notation is 9 x 10-10
Move the decimal 9 times to the right then it is 9. But the 9 is less than 10.
Moved the decimal to the right is the exponent and the exponent is negative.
Question 16.
0.00053
Answer:
Given that,
0.00053 in scientific notation is 5.3 x 10-4
Move the decimal 4 times to the right then it is 5.3. But the 5.3 is less than 10.
Moved the decimal to the right is the exponent and the exponent is negative.
For Problems 17-20, write each number in standard form.
Question 17.
3.2 × 108
Answer:
Given that the number is 3.2 × 108
108 = 100,000,000
3.2 x 100,000,000 = 320,000,000
3.2 × 108 in standard form is 320.000,000.
Question 18.
5.111 × 102
Answer:
Given that the number is 5.111 × 102
102 = 100.
5.111 x 100 = 511.1
5.111 × 102 in standard form is 511.1
Question 19.
1.06 × 10-3
Answer:
Given that the number is 1.06 × 10-3
10-3 = 0.001
1.06 x 0.001 = 0.00106
1.06 × 10-3 in standard form is 0.00106
Question 20.
7.7 × 10-9
Answer:
Given that the number is 7.7 × 10-9
10-9 = 0.000000001
7.7 x 0.000000001 = 0.0000000077
For Problems 21-24, determine which number is greater and tell how many times as great.
Question 21.
2 × 105 and 8 × 109
Answer:
Given that the numbers are
2 × 105 and 8 × 109
2 × 105 in standard form is 200000
8 × 109 in standard form is 8000000000
Therefore 8000000000/200000 = 80000
8 × 109 is the greatest number.
8 × 109 is 80000 times is greater than 2 × 105
Question 22.
3.9 × 104 and 1.3 × 10-1
Answer:
Given that the numbers are
3.9 × 104 and 1.3 × 10-1
3.9 × 104 in standard form is 39,000
1.3 × 10-1 in standard form is 0.13
Therefore 39,000/0.13 = 300,000
3.9 × 104 is the greatest number.
3.9 × 104 is 300,000 times is greater than 1.3 × 10-1
Question 23.
24,000,000 and 2.4 × 1010
Answer:
Given that the numbers are
24,000,000 and 2.4 × 1010
2.4 × 1010 in standard form is 24,000,000,000
Therefore 24,000,000,000/24,000,000 = 24,000.
2.4 × 1010 is the greatest number.
2.4 × 1010 is 24,000 times greater than 24,000,000.
Question 24.
1.5 × 10-6 and 0.0063
Answer:
Given that the numbers are
1.5 × 10-6 and 0.0063
1.5 × 10-6 in standard form is 0.0000015
Therefore 0.0063/0.0000015 = 4,200
0.0063 is the greatest number.
1.5 × 10-6 is 4,200 times greater than 0.0063
Question 25.
Social Studies The Smithsonian Institution in Washington, D.C., is the world’s largest museum, with approximately 15.4 × 107 artifacts. Explain why this number is not written in scientific notation and show how to write it correctly.
Answer:
Lesson 12.2 More Practice/Homework
Question 1.
A group of researchers in Hawaii estimated that the number of grains of sand on Earth is 7,500,000,000.000,000.000. Write this number using scientific notation.
Answer:
Given,
A group of researchers in Hawaii estimated that the number of grains of sand on Earth is 7,500,000,000.000,000.000.
We have to write 7,500,000,000.000,000.000 in scientific notation.
7,500,000,000.000,000.000 = 7.5 × 1016
Question 2.
A snail moves across a table at a rate of 0.00093 mile per hour. Write this rate in scientific notation.
Answer:
A snail moves across a table at a rate of 0.00093 mile per hour.
We have to write 0.00093 in scientific notation.
0.00093 = 9.3 × 10-4
Question 3.
Math on the Spot The approximate population of Brazil in 2008 is shown. Write this number in standard form.
Answer:
The approximate population of Brazil in 2008 is shown.
We have to write 1.86 × 108 in the standard form.
1.86 × 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 = 186000000.
For Problems 4-7, write each number in scientific notation.
Question 4.
239,000,000,000
Answer:
239,000,000,000 can be written in the scientific notation as 2.3 × 1011
Question 5.
405
Answer:
405 can be written in the scientific notation as 4.05 × 102
Question 6.
0.0000101
Answer:
0.0000101 can be written in the scientific notation as 1.01 × 10-5
Question 7.
0.00000000000006
Answer:
0.00000000000006 can be written in the scientific notation as 0.6 × 10-12
For Problems 8-11, write each number in standard form.
Question 8.
5.5 × 105
Answer:
5.5 × 105
5.5 × 10 × 10 × 10 × 10 × 10
550000
Question 9.
6.07 × 107
Answer:
6.07 × 107
6.07 × 10 × 10 × 10 × 10 × 10 × 10 × 10
60700000
Question 10.
2.04 × 10-4
Answer:
2.04 × 10-4
0.204 × 10-3
0.00204
Question 11.
4 × 10-6
Answer:
4 × 10-6
0.4 × 10-5
0.00004
For Problems 12-14, determine which number is greater and tell how many times as great.
Question 12.
7 × 1012 and 3.5 × 109
Answer:
Given that the numbers are
7 × 1012 and 3.5 × 109
7 × 1012 in standard form is 7000000000000
3.5 × 109 in standard form is 3,500,000,000.
Therefore 7000000000000/3,500,000,000 = 2000
7 × 1012 is the greatest number.
7 × 1012 is 2000 times greater than 3.5 × 109
Question 13.
1.4 × 10-5 and 2.8 × 10-4
Answer:
Given that the numbers are
1.4 × 10-5 and 2.8 × 10-4
1.4 × 10-5 in standard form is 0.000014
2.8 × 10-4 in standard form is 0.00028
Therefore 0.00028/0.000014 = 20
2.8 × 10-4 is the greatest number.
2.8 × 10-4 is 20 times greater than 1.4 × 10-5
Question 14.
16,000 and 1.6 × 108
Answer:
Given that the numbers are
16,000 and 1.6 × 108
1.6 × 108 in standard form is 160,000,000.
Therefore 160,000,000/16,000 = 10,000
1.6 × 108 is the greatest number.
1.6 × 108 is 10,000 times greater than 16,000.
Question 15.
Open-Ended Write two numbers in scientific notation so that the second number is 10 times as great as the first number.
Answer:
The first number is 1 x 101
The second number is 1 x 102
1 x 102 is 10 times greater than 1 x 101
Test Prep
Question 16.
Kendrick wants to write the number 0.000065 in scientific notation. What exponent should he use for the power of 10?
(A) -5
(B) -4
(C) 4
(D) 5
Answer:
The number 0.000065 in scientific notation is 6.5 x 10-5
Option A is the correct answer.
Question 17.
Jenna collected data about the number of annual visitors to two sports blogs. The table shows the data. The number of visitors to Sports Space is _________ times the number of visitors to Team Zone.
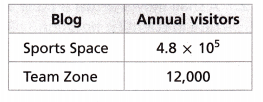
(A) 4
(B) 40
(C) 400
(D) 4000
Answer:
Given that,
The number of annual visitors to the sports space is 4.8 x 105
The number of annual visitors to the Team zone is 12,000.
4.8 x 105 in standard form is 480,000.
12,000 x 40 = 480,000.
The number of visitors to Sports Space is 40 times the number of visitors to Team Zone.
Option B is the correct answer.
Question 18.
What is 5.003 × 103 written in standard form?
(A) 0.0005003
(B) 0.005003
(C) 5003
(D) 5,003,000
Answer:
Given that,
5.003 × 103 in standard form is
103 = 1000
5.003 x 1000 = 5003
5.003 × 103 in standard form is 5003.
Option C is the correct answer.
Question 19.
Which of the following numbers is greatest?
(A) 6.1 × 107
(B) 8.9 × 106
(C) 55,000,000
(D) 9,070,000
Answer:
6.1 × 107 in standard form is 61,000,000
8.9 × 106 in standard form is 8,900,000
The greatest number is 6.1 × 107
Option A is the correct answer.
Spiral Review
Question 20.
The figure shows the dimensions of a rectangular city park. A member of the parks commission is considering a new diagonal path that would cut through the park from A to C. If the path is built, how much shorter would it be to walk along the path from A to C rather than walking along the edge of the park from A to C? Explain.
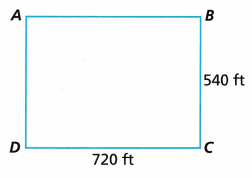
Answer:
Length = 720 ft
Width = 540 ft
We know that,
Diagonal of a rectangle = √(l² + w²)
d = √(720² + 540²) = 900
Now We have to find the distance from A to C
AC = AD + CD = 540 + 720 = 1260 ft
1260 – 900 = 360 ft
So, it is shorter to walk from A to C rather than walking along the edge of the park from A to C.
Question 21.
What is the height of the cone shown? Round to the nearest tenth of a centimeter.
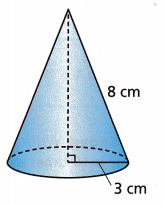
Answer:
Given that,
The height of the cone is 8cm.
8cm rounded to the nearest tenth centimeters is 10 cm.
Question 22.
Simplify the expression 70 + \(\frac{7^{2}}{\left(7^{3}\right)^{2}}\).
Answer:
70 = 1
\(\frac{7^{2}}{\left(7^{3}\right)^{2}}\) = 1/7³
70 + \(\frac{7^{2}}{\left(7^{3}\right)^{2}}\) = 1 + 1/7³