Into Math Grade 8 Module 12 Lesson 1 Answer Key Know and Apply Properties of Exponents

We included HMH Into Math Grade 8 Answer Key PDF Module 12 Lesson 1 Know and Apply Properties of Exponents to make students experts in learning maths.

HMH Into Math Grade 8 Module 12 Lesson 1 Answer Key Know and Apply Properties of Exponents

I Can use properties of integer exponents to simplify expressions.

Spark Your Learning

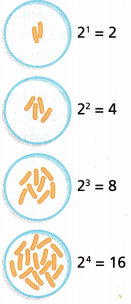
Alex has a rope that is 2⁴, or 16 feet long. He folds the rope in half and cuts it, so he now has two pieces of rope that are each 2³, or 8 feet long. Alex then folds each of the new pieces in half and cuts them, so he now has four pieces of rope that are each 2², or 4 feet long. Alex repeats this process until his pieces of rope are each 1 foot long. What would happen if Alex took each 1-foot section of rope and continued this process? What pattern do you notice?

Answer:
2⁴ = 16 feet
2³ = 8 feet
2² = 4 feet
2¹ = 2 feet
2⁰ = 1 feet

Turn and Talk Look for patterns in how these pairs are related: 2^-3 and 2³, 2^-2 and 2², 2^-1 and 2¹. What generalization can you make about a^-b, where a and b are natural numbers (1, 2, 3,…)?

Build Understanding

Question 1.
The patterns in the Spark Your Learning lead to the following two properties of exponents.

Connect to Vocabulary
The properties of exponents are rules for operations with exponents. In the power 2⁴, 2 is the base and 4 is the exponent.

If a ≠ 0 and b is an integer, then a^-b = \(\frac{1}{a^{b}}\)
If a ≠ 0, then a⁰ = 1.

A. You can look for patterns to develop the product of powers property for multiplying powers with the same base. Complete the table.


Answer:

B. How are the exponents in the left column and the exponent in the right column related?
Answer:
When the bases are equal exponents should be added.
In the left side the bases are equal the exponents are added in the right column.

C. You also can look for patterns to develop the quotient of powers property for dividing powers with the same base. Complete the table.

Answer:

D. How are the exponents in the left column and the exponent ¡n the right column related?
Answer:
Here we are using the Quotient property.
when dividing the two exponents with the same nonzero real number then the difference of the exponents with the same base.

E. Make a conjecture about two additional properties of exponents based on your findings.
Answer:
The additional property is when the bases are equal then the exponents should be added.

Turn and Talk Can you use the properties of exponents you discovered to simplify 5² • 2⁵? If so, how? If not, why not?
Answer:
Given that the expression is
5² • 2⁵
Here we are using the product property.
When multiplying the two exponents with nonzero real numbers then the powers should be added.
= 25 + 32
= 57
5² • 2⁵= 57

Step It Out

Question 2.
In 2002, a high school student broke the record for folding a sheet of paper in half multiple times. When the paper was opened, the number of regions formed was (2⁴)³. How many times did the student fold the paper? To answer, you can develop the power of a power property.
A. First look for patterns using specific examples of a power of a power. Complete the table.

Answer:

B. How are the exponents in the far-left column and the exponent in the far-right column related?
The ____________ of the exponents in the far-left column equals the ____________ in the far-right column.
Answer: The bases of the exponents in the far-left column equals the multiplication of the exponents in the far-right column.

C. Complete the conjecture about a property of exponents based on your findings:
If a ≠ 0, then .
Answer:
If an exponent is raised to other exponent, then you can multiply the two exponents.
If a≠ 0, then

D. The number of regions formed by the high school student’s folded paper was (2⁴)³. Use a single exponent to write this expression.
(2⁴)³ =
Answer:
If an exponent is raised to other exponent, then you can multiply the two exponents.
(2⁴)³ = 2¹²

E. How many times did the student fold the paper in half?
The student folded the paper _________ times. This is because 1 fold results in regions, 2 folds results in regions, and so on.
Continuing the pattern shows that ___________ folds results in regions.
Answer:
The student folded the paper for 1times. This is because 1-fold results in 2¹ regions, 2 folds results in 2²regions, and so on.
Continuing the pattern shows that 12 folds result in 2¹² regions.

Turn and Talk Does the property of exponents you discovered apply to negative powers? For example, can you use it to simplify (7^-2)²? Explain.
Answer: Yes, by using the property (a^m)ⁿ = a^m+n
(7^-2)² = 7^-2+2 = 7⁰ = 1

Question 3.
Simplify each expression.
A. 2⁴ • 2⁹

Answer:

B. 3³ • 3^-5

Answer:

C. (4 + 8)⁰

Answer:
4 + 8)⁰ = 12⁰ = 1

D. \(\frac{\left(5^{2}\right)^{5}}{5^{6}}\)

Answer:

Check Understanding

Question 1.
If a ≠ 0, what is the value of a^m • a^-m? How do you know?
Answer:
a^m • a^-m = a^m+(-m) = a⁰
= 1
If a ≠ 0 then the value of a^m • a^-m is 1.

Question 2.
Simplify 3⁰ – 3⁴ • 3^-5. Show your work and write the result as a fraction.
Answer:
Given that the expression is
3⁰ – 3⁴ • 3^-5= 1 – 81 • 0.0041152263
= 0.666

On Your Own

Question 3.
STEM According to one estimate, the number of stars in the Milky Way Galaxy is about 10² • 10³ • 10⁶.

A. Write the number of stars in the Milky Way Galaxy as a single power. Which property of exponents did you use?
Answer:
Given that the expression is
10² • 10³ • 10⁶.
Here we are using the product property.
When multiplying the two exponents with nonzero real numbers then the powers should be added.
10² • 10³ • 10⁶ = 10^{2 + 3 + 6}
= 10¹¹

B. Write the estimated number of Stars in the Milky Way Galaxy without using exponents.
Answer:
The estimated number of Stars in the Milky Way Galaxy without using exponents is 10 x 10 x 10 = 1000.

Question 4.
The formula for the volume V of a cube with edge length s is V = s³. The formula for the surface area A of the cube is A = 6s².

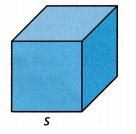
A. A cube has edges of length 2 centimeters. Write expressions using exponents for the volume of the cube (in cubic centimeters) and for the surface area of the cube (in square centimeters).
Answer:
Given that,
The length of the cube = 2 centimeters
The formula for the volume V of a cube with edge length s is V = s³
The formula for the surface area A of the cube is A = 6s².
The volume of the cube = V = 2³= 8 cubic centimetres.
The surface area of the cube = 6(2)²= 24 in square centimeters.

B. Reason What is the ratio of the cube’s volume to its surface area? Use the expressions you wrote in Part A and show how to simplify the ratio. Show your work and name any properties of exponents you use.
Answer:
The ratio of the cube’s volume to its surface area = volume of the cube/surface area = 8/24 = 0.33.

For Problems 5-7, use the table shown.

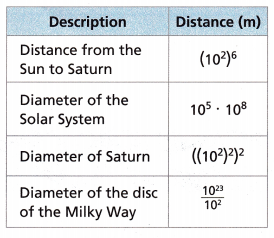
Question 5.
What is the greatest distance shown? Write it as a power of 10 with a single exponent.
Answer:
Given that,
Distance from the sun to Saturn = (10²)⁶=10¹²
Diameter of the solar system = 5² x 5⁸ =10¹⁰
Diameter of Saturn = ((7²)²)²= 7⁸
Diameter of the disc of the milky way = 10²³/10²= 10²¹
The greatest distance is the Diameter of the disc of the Milky Way= 10²¹

Question 6.
What is the least distance shown? Write it as a power of 10 with a single exponent.
Answer:
Given that,
Distance from the sun to Saturn = (10²)⁶ = 10¹²
Diameter of the solar system = 5² x 5⁸ = 10¹⁰
Diameter of Saturn = ((7²)²)² = 7⁸
Diameter of the disc of the milky way = 10²³/10² = 10²¹
The least distance shown in the power of 10 is the Diameter of the solar system = 5² x 5⁸ = 10¹⁰

Question 7.
The distance from Earth to the star Vega is approximately 10¹⁷ meters. Which of the distances in the table, if any, are less than this?
Answer:
Given that
The distance from Earth to the star Vega is approximately 10¹⁷ meters.
The distances less than Earth to the star Vega is
Distance from the sun to Saturn = (10²)⁶ = 10¹²
Diameter of the solar system = 5² x 5⁸ = 10¹⁰
Diameter of Saturn = ((7²)²)² = 7⁸

Question 8.
Open-Ended Write an expression involving two or more operations and three or more powers of 5 that can be simplified to \(\frac{1}{5}\).
Answer:
An expression involving two or more operations and three or more powers of 5 is
= (5⁰)²x(5^-1)²
= 1 x 0.2
= 0.2
= \(\frac{1}{5}\).

Question 9.
Use Repeated Reasoning You can look for patterns to develop the power of a product property.
A. Complete the table.

Answer:

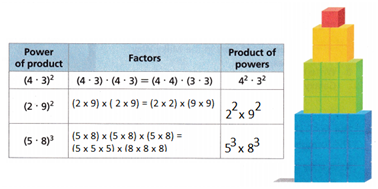
B. Look for patterns in the table. State a property of exponents based on what you observe.
Answer:
Here we are using the power of a product property.
The product of two non-zero numbers of an exponent is simplified by distributing the exponent to each number.

C. Show two different ways to simplify the expression (3 • 2)⁵.
Answer:
Given that the expression is
(3 • 2)⁵= (3)⁵• (2)⁵= 243 x 32 = 7,776
(3 • 2)⁵ =(6)⁵= 7,776

For Problems 10-13, simplify each expression. Write your answer without using exponents.

Question 10.
3² • 3⁰ • 3⁴
Answer:
Given that the expression is
3² • 3⁰ • 3⁴= 9 • 1 • 81
= 729

Question 11.
\(\frac{4^{6} \cdot 4^{-2}}{4^{5}}\)
Answer:
Given that the expression is
4⁶ • 4^-2 • 4⁵ = 4,096 • 0.0625 • 1024
= 262,144.

Question 12.
\(\frac{2^{5}}{\left(2^{2}\right)^{5}}\)
Answer:
Given that the expression is 2⁵ •  (2²)⁵
= 2⁵ • 2¹⁰
= 2¹⁰⁺⁵
= 2¹⁵
= 32,768

Question 13.
8⁰ + 8⁶ • 8^-4
Answer:
Given that,
The expression is 8⁰ + 8⁶ • 8^-4
8⁰ + 8⁶ • 8^-4= 1 + 262,144 • 0.0002441
= 65

I’m in a Learning Mindset!

What is challenging about solving a problem involving exponents? Can I work through it on my own, or do I need help?
Answer:

Lesson 12.1 More Practice/Homework

Problems 1-2 involve crayon production.

Question 1.
According to one crayon manufacturer, the average number of crayons produced in their factories each day is greater than \(\frac{10^{4} \cdot 10^{6}}{10^{3}}\).
A. Write the number of crayons as a single power of 10. Which property or properties of exponents did you use?
Answer:
Given that,
The expression is
\(\frac {10^ {4} \cdot 10^ {6} {{10^ {3}}\) = 10⁴ • 10⁶ • 10³
Here we are using the product property.
When multiplying the two exponents with nonzero real numbers then the powers should be added.
= 10⁴⁺⁶⁺³
The number of crayons = 10¹³

B. Write the number of crayons without using exponents.
Answer: The number of crayons without powers is 10 x 10 x 10 = 1000.

Question 2.
One of the boxes produced by the crayon manufacturer contains 2² • 2⁰ • 2⁴ crayons. How many crayons are in the box?
Answer:
Given that,
The crayon manufacturer contains 2² • 2⁰ • 2⁴ crayons.
= 4 x 1 x 16
= 64
There are 64 crayons in the box.

Question 3.
Katie and Lawrence collect guitar picks. Katie has (2²)⁴ guitar picks in her collection. Lawrence has (3²)² guitar picks in his collection. Who has more guitar picks? How many more?
Answer:
Given that,
Katie has (2²)⁴ guitar picks in her collection.
Lawrence has (3²)² guitar picks in his collection.
Katie has(2²)⁴= 2⁸ = 256 guitar picks
Lawrence has(3²)²= 3⁴ = 81 guitar picks
256 – 81 = 175
Katie has 175 more guitar picks.

Question 4.
Reason Simplify 3⁰ + 3⁴ • 3^-6. Show your work and explain your steps.
Answer:
Given that the expression is
3⁰ + 3⁴ • 3^-6= 1+ 81 • 0.0013717421
= 1.111

For Problems 5-8. simplify each expression.

Question 5.
8^-1 • 8^-5 • 8³
Answer:
Given that the expression is
8^-1 • 8^-5 • 8³= 0.125 • 0.00002441406 • 512
= 0.001953125
= 1/512.

Question 6.
4³ • 4^-4 • 4²
Answer:
Given that the expression is
4³ • 4^-4 • 4²= 64 • 0.00390625 • 16
= 4

Question 7.
\(\frac{9^{-2} \cdot 9^{7}}{9^{3}}\)
Answer:
Given that the expression is
\(\frac{9^{-2} \cdot 9^{7}}{9^{3}}\) = 9^-2 • 9²• 9³
= 0.0123456790 • 81• 729
= 729

Question 8.
\(\frac{\left[6^{3}\right]^{5}}{6^{18}}\)
Answer:
Given that the expression is
\(\frac{\left[6^{3}\right]^{5}}{6^{18}}\) =  (6³)⁵ • 5¹⁸
= 6^{15 ÷} 6¹⁸ = 1/6³ = 0.0046

Test Prep

Question 9.
Which expression is equivalent to 3² • 3^-8 • 3⁰?
(A) \(\frac{1}{3^{6}}\)
(B) \(\frac{1}{3^{-6}}\)
(C) 3⁶
(D) 3⁰
Answer:
Given that the expression is
3² • 3^-8 • 3⁰= 9 • 0.0001524157 • 1
= 1/729
= \(\frac{1}{3^{6}}\)
Option A is the correct answer.

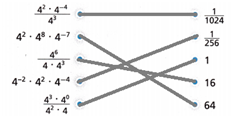
Question 10.
Draw a line to match each expression to its value.

Answer:

Question 11.
What is the value of the expression (-2 + 9)⁵ • (4 + 3)^-3 + 7⁰?
(A) \(\frac{1}{343}\)
(B) 1\(\frac{1}{49}\)
(C) 49
(D) 50
Answer:
Given that
(-2 + 9)⁵ • (4 + 3)^-3 + 7⁰
(-2 + 9)⁵ = 16,807
(4 + 3)^-3= 0.00291545
7⁰= 1
(-2 + 9)⁵ • (4 + 3)^-3 + 7⁰= 16,807 • 0.00291545 + 1
= 50
Option D is the correct answer.

Spiral Review

Question 12.
Miguel keeps track of whether or not he brought an umbrella with him to work and whether or not it actually rained that day. He collects the data and makes the two-way relative frequency table shown.

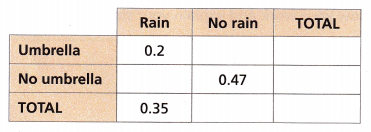
A. Complete the two-way relative frequency table.
Answer:
∑p = p1 + p2 + ….pn = 1
p1 = 0.2 + p5
p5 = p1 – 0.2 = 0.35 – 0.2 = 0.15
p2 = 1 – p1 = 0.65
p6 = p2 – 0.47 = 0.18
p3 = 0.2 + p6 = 0.38
p4 = 1 – p3 = 0.62

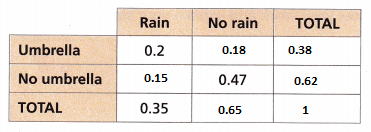
B. On what percent of the days did Miguel bring an umbrella? Which value in the table gives you this information?
Answer:

Question 13.
Solve the equation y³ = \(\frac{27}{1000}\).
Answer:
Given that,
y³ = \(\frac{27}{1000}\).
y³ = (3/10)³
y = 3/10