We included HMH Into Math Grade 8 Answer Key PDF Module 7 Lesson 4 Solve Systems by Elimination to make students experts in learning maths.
HMH Into Math Grade 8 Module 7 Lesson 4 Answer Key Solve Systems by Elimination
I Can solve a system of linear equations by elimination and check my solution.

Spark Your Learning
A football team is selling pennants and shirts. One fan bought 6 shirts and 2 pennants for $114.00. Later the fan returned 4 shirts and 2 pennants for $84.00. How could you use an operation with equations to determine the price for each shirt and each pennant?

Answer:
Given that,
Fan bought 6 shirts and 2 pennants for $114.00.
Later the fan returned 4 shirts and 2 pennants for $84.00.
4 shirts and 2 pennants = $84.
2 shirts = $114 – 84 = 30
4 shirts = 30 x 2 = 60
For 1 shirt = 60/4 = 15
For 2 pennants = $84 – $60 = 24
For each pennant = $24/2 = $12.
Turn and Talk If the fan only returned 1 shirt and 1 pennant, would you still be able to determine the price for each shirt and each pennant using the same method? Explain.
Answer:
If the fan only returned 1 shirt and 1 pennant,
For 1 shirt = 60/4 = 15
For each pennant = $24/2 = $12.
For each shirt and pennants is $15 + $12 = $27
Build Understanding
You previously learned how to solve a system of equations by replacing a variable through substitution with an equivalent expression. Elimination is the algebraic process of eliminating a variable in a system of equations by adding the equations together to eliminate one of the variables.
1. Solve the system of equations using elimination.
3x + 2y = 24
7x- 2y = 36

A. Which variable has coefficients that sum to zero? ______
Answer: Coefficients of y has that sum to zero.
B. If you add the x terms together, what is the result? ______
Answer: 3x + 7x = 10x
C. If you add the constant terms together, what is the result? _____
Answer: 24 + 36 = 60
D. Add the two equations, then solve the resulting equation.
x = ____
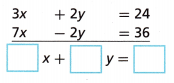
Answer:
3x + 2y = 24
7x- 2y = 36
10x = 60
x = 60/10
x = 6
E. Substitute the value of x into either original equation to solve for y.
Answer:
x = 6
3x + 2y = 24
3(6) + 2y = 24
18 + 2y = 24
2y = 24 – 18
2y = 6
y = 3
F. Write the solution as an ordered pair. ______
Answer: (6, 3)
G. Check your solution by substituting the values into both original equations.
Answer:
3x + 2y = 24
3(6) + 2(3)
18 + 6 = 24
Yes the solution is correct.
Turn and Talk In Task 1, Part E, would you get a different solution if you had substituted the value of x into the other original equation? Explain.
Step It Out
2. Solve the system of equations.
x + y = 7
2x + 4y = 18
A. Graph the system and estimate the solution.

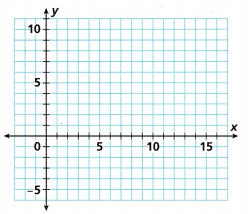
I estimate the solution is (![]() ,
, ![]() ).
).
B. Multiply the first equation by a number so that the coefficient of the x-term is the opposite of the coefficient of the x-term in the second equation.
![]() x +
x + ![]() y =
y = ![]()
2x + 4y = 18
C. Add the equations. Solve for y.
![]() y =
y = ![]()
y = ![]()
D. Use the value of y to solve for x in either original equation.
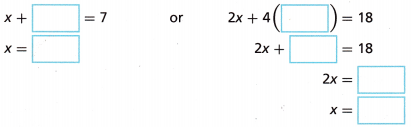
E. Check that the values of x and y make both equations true:
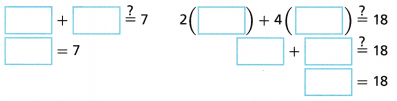
F. The solution is (![]() ,
, ![]() ).
).
Answer:
Given that the equations are
x + y = 7 is an equation 1
2x + 4y = 18 is an equation 2
From equation 1
x = 7 – y
Substitute x = 7 – y in equation 2
2(7 – y) + 4y = 18
14 – 2y + 4y = 18
14 + 2y = 18
2y = 18 – 14
2y = 4
y = 4/2
y = 2
Substitute y = 2 in equation 2
x + 2 = 7
x = 7 – 2
x = 5
The solution is (5, 2)
3. A store sells two blends of snack mix. The situation is represented by the system of equations shown
2c + 3p = 34
3c + 5p = 55
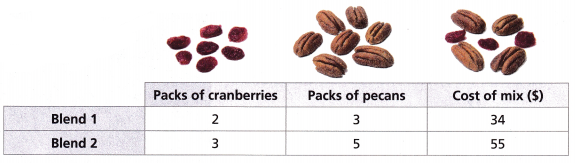
A. Is one coefficient of c a multiple of the other? ______
Is one coefficient of p a multiple of the other? _____
B. Eliminate c by multiplying the first equation by -3 and the second equation by 2, so that the new coefficients of c are opposites:
-3(2c) + -3(3p) = -3(34) → ![]() c +
c + ![]() p =
p = ![]()
2(3c) + 2(5 p) = 2(55) → ![]() c +
c + ![]() p =
p = ![]()
Answer:
-3(2c) + -3(3p) = -3(34) → -6c + (-9)p = -102
2(3c) + 2(5 p) = 2(55) → 6c + 10p = 110
C. Add the equations and solve.
![]() p =
p = ![]()
p = ![]()
Answer:
1p = 8
p = 8
D. Use the value of p to solve for c in either equation.
2c + 3![]() = 34
= 34
2c + ![]() = 34
= 34
2c = ![]()
c = ![]()
The pecans cost ____ per pack and the cranberries
cost ____ per pack.
Answer:
2c + 3p = 34
2c + 3p = 34
2c = 34 – 3p
c = 34 – 3p/2
Check Understanding
Question 1.
The system of equations shown represents the length and width in centimeters of a rectangle. What are the length and width?
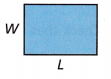
2L + 2W= 52
L – W = 2
Answer:
2L + 2W= 52
L – W = 2— × 2 = 2L – 2W = 4
Solve 1 & 2
2L + 2W= 52
2L – 2W = 4
4L = 56
L = 14
Substitute L in eq.
L – W = 2
14 – W = 2
W = 14 – 2
W = 12
Question 2.
What is the solution to the given system of equations?
3x – y = 2
3x – 2y = 10
Answer:
Given that the equations are
3x – y = 2 is an equation 1
3x – 2y = 10 is an equation 2
From equation 1
-y = 2 – 3x
y = -2 + 3x
Substitute y value in equation 2
3(-2 + 3x) – 2y = 10
-6 + 9x – 2y = 10
7y = 10 + 6
7y = 16
y = 16/7
y = 2.28
Substitute y = 2.28 in equation 1
3x – 2.28 = 2
3x = 2 + 2.28
3x = 4.28
x = 4.28/3
x = 1.42
The solution is (1.42, 2.28)
On Your Own
Question 3.
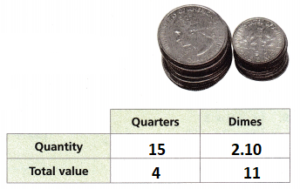
Gareth has 15 total quarters and dimes with a total value of $2.10. The system of equations shown can be used to solve for the number of each Gareth has.

Q + D = 15
25Q + 10D = 210
Complete the table to show the quantities and values of the coins Gareth has.
Answer:
Given that,
Q + D = 15
25Q + 10D = 210
10(Q + D) + 15Q = 210
10(15) + 15Q = 210
150 + 15Q = 210
15Q = 210 – 150
15Q = 60
Q = 60/15
Q = 4
Substitute Q = 4 in Q + D = 15
Q + D = 15
4 + D = 15
D = 15 – 4
D = 11
The total values of Quarters is 4
The total values of Dimes = 11
Question 4.
Liliana spends $4.00 on 2 boxes of popcorn and 2 drinks. Nadette spends $5.25 on 2 boxes of popcorn and 3 drinks. The prices of the popcorn and drinks can be determined by solving the system of equations shown.
2p + 2d = 4.00
2p + 3d = 5.25
A. What variable will you eliminate first? How?
Answer:
Given that the equations are
2p + 2d = 4.00
2p + 3d = 5.25
Eliminate the p variable.
B. What is the solution to the system?
Answer:
Given that the equations are
2p + 2d = 4.00 is an equation 1
2p + 3d = 5.25 is an equation 2
Subtract equation 2 from equation 1 then we get
-d = -1.25
d = 1.25
Substitute d = 1.25 in equation 1
2p + 2(1.25) = 4.00
2p + 2.5 = 4.00
2p = 4.00 – 2.5
2p = 1.5
p = 1.5/2
p = 0.75
The solution is (1.25, 0.75)
C. What is the price of a box of popcorn? a drink?
Answer:
The solution is (1.25, 0.75)
The price of popcorn is 0.75
The price of the drinks is 1.25.
Question 5.
Construct Arguments Consider the system of equations.
x + y = 6
x – y = 12
A. To solve by elimination, which variable would you eliminate and why?
__________________
Answer:
Given that the equations are
x + y = 6
x – y = 12
Here eliminates the x variable, then we get
2y = -6
y = -6/2
y = -3
B. Will the solution be different if substitution is used instead of elimination? Explain.
__________________
Answer:
The solution cannot be different if substitution is used instead of elimination.
While substitution of elimination we get the same solution.
Question 6.
What is the solution to the system?
3x + 2y = 37
7x – 6y = 1
Answer:
Given that the equations are
3x + 2y = 37 is an equation 1
7x – 6y = 1 is an equation 2
Multiplying equation 1 with 7 and equation 2 with 3 then we get
21x + 14y = 259 is an equation 3
21x – 18y = 3 is an equation 4
Subtract equation 4 from equation 3
32y = 256
y = 256/32
y = 8
Substitute y = 8 in equation 1
3x + 2(8) = 37
3x + 16 = 37
3x = 37 – 16
3x = 21
x = 21/3
x = 7
The solution is (7, 8).
For Problems 7-10, solve the system of equations using elimination.
Question 7.
3x – 2y = 5
x + 2y = 3
Answer:
Given that the equations are
3x – 2y = 5 is an equation 1
x + 2y = 3 is an equation 2
From equation 2
x = 3 – 2y
Substitute x in equation 2
3(3 – 2y) – 2y = 5
9 – 6y – 2y = 5
9 – 8y = 5
-8y = 5 – 9
-8y = -4
y = -4/-8
y = 1/2
y = 0.5
Substitute y = 0.5 in equation 2
x + 2(0.5) = 3
x + 1 = 3
x = 3 – 1
x = 2
The solution is (2,0.5)
Question 8.
4x + 3y = 3
4x – 2y = 18
Answer:
Given that the equations are
4x + 3y = 3 is an equation 1
4x – 2y = 18 is an equation 2
Subtract equation 2 from equation 1
5y = -15
y = -15/5
y = -3
Substitute y = -3 in equation 1
4x + 3(-3) = 3
4x – 9 = 3
4x = 3 + 9
4x = 12
x = 12/4
x = 3
The solution is (3, -3).
Question 9.
x – y = 3
2x + 2y = 50
Answer:
Given that the equations are
x – y = 3 is an equation 1
2x + 2y = 50 is an equation 2
From equation 1
x = 3 + y
Substitute x in equation 2
2(3 + y) + 2y = 50
6 + 2y + 2y = 50
6 + 4y = 50
4y = 50 -6
4y = 44
y = 44/4
y = 11
Substitute y = 11 in equation 1
x – 11 = 3
x = 3 + 11
x = 14
The solution is (14, 11).
Question 10.
3x + 5y = 22.5
5x + 3y = 17.5
Answer:
Given that the equations are
3x + 5y = 22.5 is an equation 1
5x + 3y = 17.5 is an equation 2
Multiply equation 1 with 5 and equation 2 with 3.
15x + 25y = 112.5 is an equation 3
15x + 9y = 52.5 is an equation 4
Subtract equation 4 from equation 3 then we get
16y = 60
y = 60/16
y = 3.75
Substitute y = 3.75 in equation 1
3x + 5(3.75) = 22.5
3x + 18.75 = 22.5
3x = 22.5 – 18.75
3x = 3.75
x = 3.75/3
x = 1.25
The solution is (1.25, 3.75)
Question 11.
STEM A chemist uses the system of equations shown to find the amounts of pure water and salt water needed to make a new solution.
x + y = 80
x + 0.25y = 32

A. Graph the system and estimate the solution.
Answer:
B. Solve the system for the precise answer. How many liters of pure water did the chemist use? How many liters of salt water?
Answer:
Given that the equations are
x + y = 80
x + 0.25y = 32
Subtract equation 2 from equation 1
0.75 y = 48
y = 48/0.75
y = 64
substitute y = 64 in equation 1
x + 64 = 80
x = 80 – 64
x = 16
The solution is (16, 64).
Therefore 16 litters of pure water are used and 64 litters of salt water is used.
Question 12.
Open Ended Complete the system of equations so that it has a solution of (4, 7).
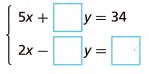
Answer:
I’m in a Learning Mindset!
How was solving systems by elimination a challenge for me? Is it still a challenge?
Lesson 7.4 Mre Practice/Homework
Question 1.
A rectangular box has a perimeter of 76 inches. If two of the boxes are placed next to each other on the long side, the new box is a rectangular shape with a perimeter of 112 inches.

The system represents the perimeters of the boxes:
2L + 2W= 76
12L + 4W= 112
What are the dimensions of the original box?
__________________
Answer:
Given that
The perimeter of the rectangle = is 76 inches
The perimeter of the newly formed rectangle = is 112 inches.
The dimensions of the original box are
2L + 2W= 76 i
2(L + W) = 76 is an equation 1
When two rectangular boxes are placed side by side then we can form a newly rectangle
The perimeter of the newly rectangle is 2(L + B) + 2(L + B) + 2L = 112
76 + 76 + 2L = 112
156 – 2L = 112
-2L = 112 – 156
2L = 40
L = 20
Substitute L = 20 in equation 1
2(20 + B) = 76
40 + 2B = 76
2B = 76 – 40
2B = 36
B = 36/2
B = 18
The original dimensions of the rectangle are
Length = 20
Breadth = 18.
Question 2.
Math on the Spot Solve the system by eliminiation.
2x + 5y = 4
2x – y = -8
A. Which variable would you eliminate to solve the system using elimination? Explain.
Answer:
Given that the equations are
2x + 5y = 4 is an equation 1
2x – y = -8 is an equation 2
Here we are eliminating the x variable.
For subtracting the x variable subtract equation 2 from equation 1
Then we get
6y = 12
B. What is the solution to the system?
Answer:
Given that the equations are
2x + 5y = 4 is an equation 1
2x – y = -8 is an equation 2
Subtract equation 2 from equation 1
Then we get
6y = 12
y = 12/6
y = 2
Substitute y = 2 in equation 1
2x + 5(2) = 4
2x + 10 = 4
2x = 4 – 10
2x = -6
x = -6/2
x = -3.
The solution is (-3, 2).
Question 3.
Critique Reasoning Carsen incorrectly solved a system of equations. His first step is shown. His first step is shown.
6x + 5y = 36 → 6x + 5y = 36
3x – 2y = -9 → -6x – 4y = 18
What was Carsen’s error? What is the correct solution to the system?
Answer:
Given that the equations are
6x + 5y = 36 → 6x + 5y = 36
3x – 2y = -9 → -6x – 4y = 18
Carsen’s error is that multiplying equation 2 with -2 is the wrong step.
The correct solution is
6x + 5y = 36 is an equation 1
3x – 2y = -9 is an equation 2
Multiply equation 2 with 2 then we get
6x – 4y = -18. Is an equation 3
Subtract equation 3 from equation 1
9y = 54
y = 54/9
y = 6
Substitute equation y = 6 in equation 1
6x + 5(6) = 36
6x + 30 = 36
6x = 36 – 30
6x = 6
x = 6/6
x = 1
The solution is (1, 6).
For Problems 4-7. solve the system of equations by elimination.
Question 4.
2x – 3y = 2
-2x – y = -26
Answer:
Given that the equations are
2x – 3y = 2 is an equation 1
-2x – y = -26 is an equation 2
From equation 2
-y = -26 + 2x
y = 26 – 2x
Substitute y value in equation 1
2x – 3(26 – 2x) = 2
2x – 78 + 6x = 2
8x – 78 = 2
8x = 2 + 78
8x = 80
x = 80/8
x = 8
Substitute x = 8 in equation 2
-2(8) – y = -26
-16 – y = -26
-y = -26 + 16
-y = -10
y = 10
The solution is (10, 8).
Question 5.
4x + y = -16
2x – 3y = -8
Answer:
Given that the equations are
4x + y = -16 is an equation 1
2x – 3y = -8 is an equation 2
From equation 1
y = -16 – 4x
Substitute the y value in equation 2
2x – 3(-16 – 4x) = -8
2x + 48 + 12x = -8
14x + 48 = -8
14x = -8 – 48
14x = -56
x = -56/14
x = -4
Substitute x = -4 in equation 1
4(-4) + y = -16
-16 + y = -16
y = -16 + 16
y = 0
The solution is(-4, 0).
Question 6.
7x + 2y = 28
3x + 2y = 20
Answer:
Given that the equations are
7x + 2y = 28 is an equation 1
3x + 2y = 20 is an equation 2
Subtract equation 2 from equation 1 then we get
4x = 8
x = 8/4
x = 2
Substitute x in equation 1
7(2) + 2y = 28
14 + 2y = 28
2y = 28 – 14
2y = 14
y = 14/2
y = 7
The solution is (2, 7).
Question 7.
3x + 4y = 1
5x + 3y = -2
Answer:
Given that the equations are
3x + 4y = 1 is an equation 1
5x + 3y = -2 is an equation 2
Multiply equation 1 with 5 and multiply equation 2 with 3 then we get
15x + 20y = 5 is an equation 3
15x + 9y = -6 is an equation 4
Subtract equation 4 from equation 3
11y = 11
y = 11/11
y = 1
Substitute y = 1 in equation 1
3x + 4(1) = 1
3x + 4 = 1
3x = 1 – 4
3x = -3
x = -3/3
x = -1
The solution is (-1, 1).
Test Prep
Question 8.
Bailey and Miranda sell ads for the school yearbook. Their first month’s sales totals are represented by the system shown, where x is the price of a small ad and y is the price of a full-page ad. What are the prices of small ads and of full-page ads?
14x + 5y = 975
10x + 4y = 750
small ad: $![]()
full-page ad: $![]()
Answer:
Given that the equations are
14x + 5y = 975 is an equation 1
10x + 4y = 750 is an equation 2
Multiply equation 1 with 10 and equation 2 with 14 then we get
140x + 50y = 9,750 is an equation 3
140x + 56y = 10,500 is an equation 4
Subtract equation 4 from equation 3
-6y = – 750
y = – 750/-6
y = 125
Substitute y = 125 in equation 1
14x + 5(125) = 975
14x + 625 = 975
14x = 975 – 625
14x = 350
x = 350/14
x = 25
The solution is (25, 125)
Therefore, Small ad = $25
Full page ad = $125.
Question 9.
What is the y-coordinate of the solution to the system of equations shown?
2x + 3y = 5
3x – 2y = -12
A. -3
B. -2
C. 2
D. 3
Answer:
Given that the equation are
2x + 3y = 5 is an equation 1
3x – 2y = -12 is an equation 2
Multiply equation 1 with 3 and equation 2 with 2 then we get
6x + 9y = 15 is an equation 3
6x – 4y = -24 is an equation 4
Subtract equation 4 from equation 3
13y = 39
y = 39/13
y = 3
The y coordinate is 3
Option d is the correct answer.
Question 10.
A triangle has two congruent angles and one unique angle. The system of equations shown represents the relationship between the angle measures. What are the measures of the angles in the triangle?
2x + y = 180
x – y = 30
Answer:
Given that,
The equations are
2x + y = 180 is an equation 1
x – y = 30 is an equation 2
From equation 2
x = y + 30
2(y + 30) + y = 180
2y + 60 + y = 180
3y = 180 – 60
3y = 120
y = 120/3
y = 40
Substitute y in equation 2
x – 40 = 30
x = 30 + 40
x = 70
The solution is (70, 40).
Therefore the angles in the triangle are 70 degrees, 80 degrees.
Spiral Review
Question 11.
Explain how similar triangles can be used to prove the slope of the line is the same through Points A(0, 3) and 6(2, 8) as through 6(2, 8) and C(6, 18).
Answer:
Question 12.
What is the equation of the line through the points (4, 6), (8, 12), and (10, 15)?
Answer:
Question 13.
What is the domain of the function with points (-2, 4), (-1, 1), (0, 0), (1, 1), and (2, 4)?
Answer:
The domain and the range are defined as the relation.
Consider the points in the relation.
R = { (-2, 4), (-1, 1), (0, 0), (1, 1), (2, 4)}
Domain = the set of all the x coordinates.
Domain = {-2, -1, 0, 1, 2}.