Into Math Grade 7 Module 14 Lesson 4 Answer Key Use Experimental Probability and Proportional Reasoning to Make Predictions

We included HMH Into Math Grade 7 Answer Key PDF Module 14 Lesson 4 Use Experimental Probability and Proportional Reasoning to Make Predictions to make students experts in learning maths.

HMH Into Math Grade 7 Module 14 Lesson 4 Answer Key Use Experimental Probability and Proportional Reasoning to Make Predictions

I Can use proportional reasoning or percent expressions to make a prediction based on an experimental probability.

Step It Out

Question 1.
Jessica bowls in several leagues, and she is very good at closing out frames. Over the past few years, she has closed out 8 of every 10 frames she has bowled. This season Jessica will bowl 35 games, or 350 frames. How many frames can Jessica expect to close out this season?

A. Method 1: Use a proportion.
Write a proportion: 8 out of 10 is how many out of 350?

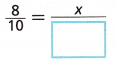
Multiply \(\frac{8}{10}\) by a form of 1 to keep the equation true and to find the value of x.

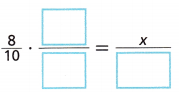
The value of x is 8 • = .
Answer:

B. Method 2: Use a percent expression.
Write \(\frac{8}{10}\) as a percent and a decimal: % and .
Find % of 350: • 350, or .
So Jessica can expect to close out about ___________ frames.
Answer:

Connect to Vocabulary
A proportion is an equation that states that two ratios are equivalent. Multiplying the numerator and denominator of one of the ratios by the same, correctly chosen number will yield the other ratio.

C. If Jessica closes out 288 frames this season, was her average over few years a good predictor of her performance?
Answer:

Turn and Talk Which method do you prefer for making a prediction, using a proportion or a percent? Explain.
Answer:

Question 2.
The middle school that Carmen and Richard attend has 925 students. The schedule options for first period include only math and English. In order to find out whether students prefer first period math or first period English, Carmen and Richard took a poll of 100 randomly selected students. The results are shown.

A. Method 1
Use proportional reasoning to predict the number of students in the whole school who will state that they prefer first-period math.
___________ out of 100 is how many out of 925?

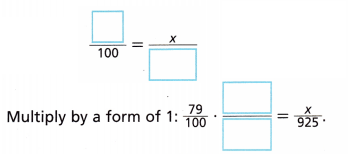
The value of x is 79 • =
About ___________ students will state that they prefer first period math.
Answer:

B. Method 2
Use a percent to predict the number of students in the whole school who will state that they prefer first period math.
79 out of 100 is ___________%, so find ___________% of ___________, the number of students in the whole school.
• 925 = .
About _________ students will state that they prefer first period math.
Answer:

C. Find the number of students who will state that they prefer first period English without using proportional reasoning or a percent. This is the complement of the event from Parts A and B.
Subtract the number of students who will state that they prefer first period math from the total number of students in the school.
925 – =
A reasonable prediction of students in this school who will state that they prefer first period English is _______ students.
Answer:

Turn and Talk Explain why the answers were rounded to whole numbers in this task.
Answer:

Question 3.
A company analyzes the page views of visitors that come to its website. Based on a sample, the company determines that 30% of all visitors click away from the site after viewing only the home page. The company gets an average of 1,173 visitors per week. Use proportional reasoning to predict how many visitors will leave the website next week after visiting only the home page.

The value of x is 30 • = .
Because the number describes the number of people, it should be a whole number. So the prediction is that about people leave the site after visiting only the home page.
Answer:

Turn and Talk The company’s president claims that they are losing about 450 visitors per week who click away after seeing only the home page. Is this a reasonable claim? Explain.
Answer:

Check Understanding

Question 1.
A random sample of patients at a medical office found that 40% were in the age range 13-21. There are 1,100 patients in total. Use the experimental probability from the survey to predict about how many patients are in the age range 13-21.
Answer:

Use the following information for Problems 2-3.

A company sold 660 watches. A consumer advocate group found that 5% of this particular type of watch was defective when they conducted a random survey of 100 watches.

Question 2.
Estimate the number of watches sold that were defective.
Answer:

Question 3.
Estimate the number of watches sold that were not defective.
Answer:

On Your Own

Question 4.
Model with Mathematics In a sample of 100 randomly selected concert attendees, the concert organizers find that 11 of them left the show early. The concert originally had 2,040 attendees.

A. Use proportional reasoning to estimate how many of the total number of attendees left the concert early.
Answer:

B. Attend to Precision Explain why the answer in Part A cannot be a decimal.
Answer:

C. Suppose there are 3 concerts at this hall next week, and the total attendance will be 5,500. Use a percent expression to predict the number of these attendees who will leave a concert early next week.
Answer:

Question 5.
Model With Mathematics In D’Andre’s class, 5 of the 25 students are 5 feet tall or shorter. There are 400 students in D’Andre’s grade at his school.
A. Set up a proportional relationship to estimate the total number of students who are 5 feet tall or shorter in D’Andre’s grade, based on the experiment probability from the survey of his class.
Answer:

B. Estimate how many students in D’Andre’s grade are over 5 feet tall.
Answer:

Question 6.
STEM According to the US Forest Service, the most common tree type found in timberlands in the state of Florida is the longleaf pine tree. In a sample population, 35% of trees were of this type.

A. Write a percent expression to estimate the number of acres of longleaf pine trees in Florida.
Answer:

B. Evaluate the percent expression to estimate how many acres of long leaf pine trees there are in Florida.
Answer:

Question 7.
A survey was conducted among middle school students asking, “Do you prefer vanilla or chocolate ice cream?” The results are shown.

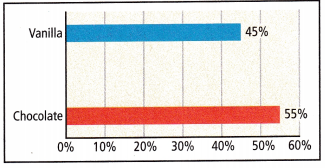
A. Write both a proportion and a percent expression to estimate how many students prefer chocolate in a population of 700.
Answer:
Proportion of chocolate in the population is 55%/60% = x/700.
0.91 x 700 = x
x = 637.
The students prefer 637 chocolate in a population of 700.

B. Estimate how many students out of 700 prefer chocolate ice cream.
Answer: The students prefer chocolate ice cream out of 700 out of 637.

For Problems 8-11, the following samples were taken to see how many people preferred Candidate A. Estimate the number of people who prefer Candidate A based on the information given.

Question 8.
Sample size: 200
Number of favorable responses: 100
Population: 1,000
Answer:

Question 9.
Sample size: 100
Percent favorable: 35%
Population: 1,800
Answer:

Question 10.
Sample size: 100
Number of favorable responses: 22
Population: 450
Answer:

Question 11.
Sample size: 100
Percent favorable: 90%
Population: 2,100
Answer:

Question 12.
Construct Arguments Steven tossed a coin loo times. It came up heads 52 times and tails 48 times. Based on this sample, write a percent expression and predict how many times heads would occur if Steven tossed the coin 1,000 times. This is not the expected 500 times (or 50%). Explain the discrepancy.
Answer:

Question 13.
Aman sometimes receives undeliverable messages on her e-mail. Of the last 100 e-mails that she sent, 6 of them came back as undeliverable. She sends an average of 750 e-mails in a month. How many undeliverable messages should Aman expect to receive in one month?
Answer:

Question 14.
Social Studies Jiang was concerned about a particularly busy intersection because it did not have a stop sign. She took a survey of 100 people who used that intersection. Seventy-five people she spoke to support putting in a stop sign. The town’s population is 4,480. Write a percent expression and a proportion to estimate how many people in the town support the stop sign. Then make an argument as to why Jiang’s survey results may not be a good predictor of town opinion.
Answer:

Question 15.
Attend to Precision Luis used proportional reasoning to predict that the number of people riding buses past his window each day would be 100.6 people. How should he express his answer? Explain.
Answer:

For Problems 16-17, use this information.

Of 100 students and teachers in Claire’s school, the number of people who have each birthstone are shown. The school has 510 teachers and students.

Garnet (January): 6
Amethyst (February): 15
Aquamarine (March): 8
Diamond (April): 9
Emerald (May): 9
Pearl (June): 7
Ruby (July): 11
Peridot (August): 6
Sapphire (September): 8
Opal (October): 4
Topaz (November): 10
Tanzanite (December): 7

Question 16.
Write and evaluate a percent expression to estimate the total number of teachers and students at the school who have amethyst as their birthstone.
Answer:

Question 17.
Write and solve a proportion to estimate how many more teachers and students at the school have garnets than opals as their birthstone.
Answer:

Lesson 14.4 More Practice/Homework

Question 1.
Ms. Kalidova asked her class to use a percent expression to predict the result of the upcoming election for class president of the seventh grade. Results of a poll conducted of 50 students are provided in the graph. Assume the seventh grade has 350 students and everyone votes for one of the two candidates. Write a percent expression and evaluate it to find the number of votes Andrew should expect to receive.

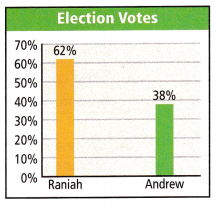
Answer:

Question 2.
Open-Ended Write a real-world problem involving a sample and a population that can be modeled by the proportion: \(\frac{66}{100}\) = \(\frac{x}{2,500}\).
Answer:
\(\frac{66}{100}\) = \(\frac{x}{2,500}\)
66/100 = x/2500
66 × 25 = x
x = 1650

Question 3.
Shane plays baseball. The chart shows the results of his first 100 times at bat. Write a proportion and solve it to predict the number of home runs Shane will hit in his next 460 times at bat.

Answer:
Given,
Shane plays baseball. The chart shows the results of his first 100 times at-bat.
There are 5 home runs in his first 100 times.
So, the probability of home runs = 5/100 = 1/20
Then in his next 460 times at-bat, the number of home runs is
460 × 1/20 = 23
Thus we can predict that the number of home runs is 23.

Question 4.
Math on the Spot Professor Burger found that the experimental probability of his making a strike in bowling is 20%. Out of 400 throws, about how many could he predict would be strikes?
Answer:

Model with Mathematics For Problems 5-6. use the following scenario.

In one weekend, 1,200 people attend a play at the theater downtown. A survey of 100 people who attended found that 45 gave the play at least 4 stars out of 5. Write and use the indicated model to estimate how many people in all would give the play at least 4 stars.

Question 5.
Solve using a proportion.
Answer:
Given,
In one weekend, 1,200 people attend a play at the theater downtown.
A survey of 100 people who attended found that 45 gave the play at least 4 stars out of 5.
45/100 = 0.45
0.45 × 1200 = 540

Question 6.
Solve using a percent expression.
Answer:
45% of 1200
45/100 × 1200 = 540

Test Prep

Question 7.
The chart shows the number of hours each student spends training for their favorite sport, per 100 hours.

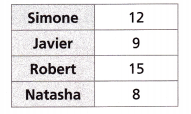
A. Write a proportion and make a prediction for the number of hours Simone will spend training over a 2,000-hour period.
Answer:
12/100 = x/2000
12 × 2000 = 100x
24000 = 100x
x = 24000/100
x = 240 hours

B. Write and use a percent expression to predict the number of hours Javier will spend training over a 2,000-hour period.
Answer:
9/100 = x/2000
9 × 2000 = 100x
18000 = 100x
x = 18000/100
x = 180 hours

Question 8.
Jabrin was tossing a ball up in the air and catching it. He found that in 50 tries, he could catch it 45 times. He is going to do this 33 more times. Predict how many times Jabrin will catch the ball out of these 33 tosses.
Answer:
Given,
Jabrin was tossing a ball up in the air and catching it.
He found that in 50 tries, he could catch it 45 times.
p = 45/50 = 90%
Thus he has a 90% probability that he will catch the ball
90% (50 + 33)
90% × 83 = 74.7 ≈ 75
75 – 45 = 30
Therefore he might catch the ball 30 times.

Question 9.
Considering the proportions/percent equations and the corresponding values of x given, which combination is correct?
(A) \(\frac{40}{100}\) = \(\frac{x}{900}\); x = 49
(B) 0.20(1,200) = x; x = 300
(C) \(\frac{25}{100}\) = \(\frac{x}{750}\); x = 175
(D) 0.70(500) = x; x = 350
Answer:

Spiral Review

Question 10.
A vegetarian restaurant offers 52 vegetarian meals on its menu. Four of the meals include eggplant. Shan picks a dish at random from the menu with his eyes closed. What is the probability that he orders a meal that does not include eggplant? Write the probability as a fraction.
Answer:
Given that,
A vegetarian restaurant offers 52 vegetarian meals on its menu.
Meals include 4 eggplants.
Meals not include eggplant = 52 – 4 = 48
The probability that he orders a meal that does not include eggplant = 48/54 = 8/9 = 0.88.

Question 11.
Jake is saving for a new tablet. It costs $250, and he has $100. He earns $5 per week for doing chores. Jake wants to figure out how many weeks it will take for him to have at least enough money to buy a new tablet. Write an inequality and solve it to determine the number of weeks it will take.
Answer:
Given that,
The total cost of new tablet = $250
Jake has $100.
Jake earns $5 per week
Let us consider number of weeks = x
The inequality equation is
$100 + 5x = $250.
5x = $250 – $100
5x = $150
x = $150/5
x = 30
Therefore Jake wants to work for 30 weeks to buy the tablet.