We included HMH Into Math Grade 7 Answer Key PDF Module 14 Lesson 3 Find Experimental Probability of Compound Events to make students experts in learning maths.
HMH Into Math Grade 7 Module 14 Lesson 3 Answer Key Find Experimental Probability of Compound Events
I Can find the experimental probability of a compound event.
Spark Your Learning
Felix was attending an awards dinner and the menu had the choices shown for appetizer and entree. What is the sample space for his dinner selection?

Answer:
Sample space means the total number of possible outcomes.
The menu had the choices shown for appetizers and entrees.
The sample space for the dinner is {appetizer, entree}.
Turn and Talk The menu also had a choice of two drinks. When considering that choice, how does that affect the total number of combinations that are available to order?
Answer:
The menu adds a choice of two drinks,
The sample space for the dinner is {appetizer, entree, two drinks}.
It affects the total number of combinations that are available to order.
Before we have only 2 choices after adding the 2 drinks, we have the 4 choices.
Build Understanding
At Felix’s awards dinner, T-shirts were being handed out to the award winners. The choices for the shirts are shown. The selection of a shirt is a compound event due to the available choices in different categories.
Connect to Vocabulary
A coin landing heads up when flipped or rolling a 6 on a number cube are simple events. A compound event is an event that includes two or more simple events.
Question 1.
Define the sample space of the shirt choices.

A. How many colors are there? What are the choices?
Answer: There are 3 colors and 3 choices.
B. How many sizes are there? What are the choices?
Answer: There are 3 sizes and 3 choices.
C. Write all the possible combinations of sizes and colors.
Answer: The combination of sizes and colors is
(red, small), (red, large), (red, medium).
(blue, small), (blue, large), (blue, medium).
(green, small), (green, large), (green, medium).
D. There are _____________ possible outcomes for this compound event.
Answer: There is 9 possible outcomes for this compound event.
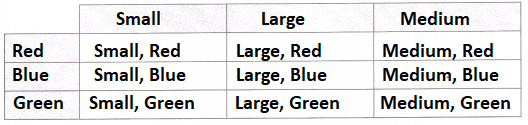
E. In the table, fill out the shaded boxes with headings for the possible sizes and colors of the shirts. Then fill in the table to show the sample space, all the possible outcomes when a shirt is selected.

Answer:
The combination of sizes and colours is
(red, small), (red, large), (red, medium).
(blue, small), (blue, large), (blue, medium).
(green, small), (green, large), (green, medium).
F. Suppose a compound event includes two simple events. Explain how many rows and columns are needed in a table of the sample space.
Answer: The compound event includes two simple events.
You needed 2 columns and 2 rows in a table of the sample space.
Turn and Talk Does it matter whether sizes or colors are listed in rows or columns? Explain.
Answer:
Step It Out
Conducting a survey is a type of experiment. Each time a question is asked of one person counts as one trial. Each answer is an outcome. Compare the number of times one answer is given to the total number of times a question is asked to find the experimental probability that a new, randomly chosen person, if asked, will give this answer.
Question 2.
Guests at the awards were asked for their dinner order. The number of people who gave each answer are shown. Find the experimental probability that a dinner guest orders roast beef and salad.
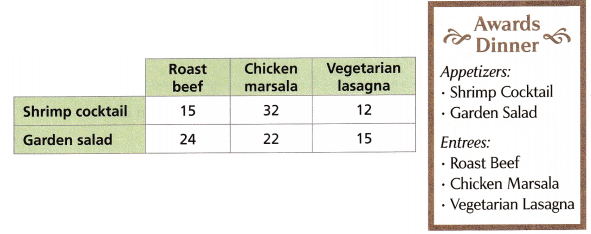
A. Find the total number of dinner orders.
15 + 32 + ![]() + 24 + 22 + 15 =
+ 24 + 22 + 15 = ![]()
Answer: The total number of dinner orders is 15 + 32 + 12 + 24 + 22 + 15 = 120.
B. Find the experimental probability.
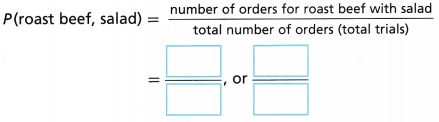
Answer:
Given that,
Roast beef = 15
Salad = 14
P (roast beef, salad) = number of orders for roast beef with salad/ total number of orders = 39/120 = 13/40
Question 3.
The T-shirt choices of some award winners are shown in the table. What is the experimental probability that an award winner does NOT select a medium green T-shirt?
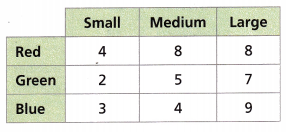
A. Find the experimental probability of choosing a medium green T-shirt.
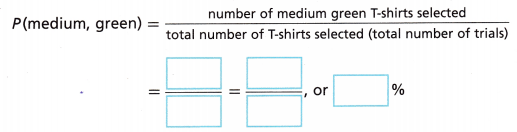
Answer:
The number of green medium green T-shirts = 5
The total number of green T-shirts = 4 + 2 + 3 + 8 + 5 + 4 + 8 + 7 + 9 = 50
P(medium, green) = number of medium green t-shirts selected/ total number of T – shirts selected = 5/50 = 1/10 or 10%.
B. Find the complement of the event in Part A, the experimental probability of NOT choosing a medium green T-shirt.
P(NOT medium, green) = 1 – P(medium, green)

Answer:
The number of green medium green T-shirts = 5
The total number of green T-shirts = 4 + 2 + 3 + 8 + 5 + 4 + 8 + 7 + 9 = 50
P(NOT medium, green) = 1 – P(medium, green)
P(medium, green) = number of medium green t-shirts selected/ total number of T – shirts selected = 5/50
Therefore 1 – 5/50 = 45/50 or 90%
Question 4.
A party bundle sold by an event planning company contains party favors and table decorations. The party favor choices are key chains, pens, or wristbands. The table decoration choices are flowers or candles. The company packs party bundles and stores them in a warehouse, choosing the party favor and decorations for each bundle at random. Tatiana simulates choosing a bundle from the warehouse and checking its contents.

A. List the compound events that occur when checking the bundles.
Answer:
B. Describe the two choices that together make up each compound event.
Answer:
C. How can you use a number cube and a coin to simulate the experiment?
Answer:
D. Tatiana simulates 100 trials of the experiment and records the results shown in the table. What is the experimental probability that the next choice of a bundle includes pens and candles?
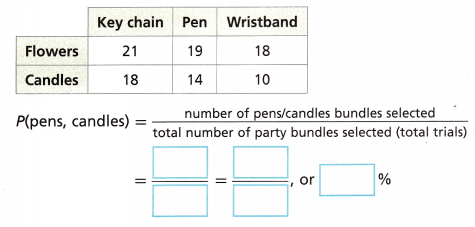
Answer:
Check Understanding
A restaurant manager records the choices made at breakfast. The table shows the average daily breakfast orders for toast.
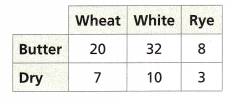
Question 1.
How many possible outcomes are in the sample space of toast choices?
Answer:
The possible outcomes are (wheat, butter), (whites, butter), (rye, butter), (wheat, dry), (white, dry), (rye, dry).
There are 6 possible outcomes are in the sample space of toast choices.
Question 2.
What is the experimental probability that a new customer orders buttered white toast? Write your answer as a fraction and a percent.
Answer:
The customer orders buttered white toast.
The number of possible outcomes is 6
The experimental probability of buttered white toast = number of events occurring/ total number of trials = 1/6. Or 16%
On Your Own
Question 3.
A tea bar offers tea in the varieties shown.

A. How many rows and columns represent the sample space?
Answer: There are 3 rows and 2 columns representing the sample space.
B. How many possible outcomes are in the sample space?
Answer: The possible outcomes are (Hibiscus tea, small), (Macha tea, small), (black tea, small), (Hibiscus tea, large), (Macha tea, large), (Black tea, large).
There are 6 possible outcomes in the sample space.
Question 4.
Model with Mathematics Sabah works at a movie theater. One evening, she tracks the popcorn orders at the concessions stand.
A. Sabah sold 125 orders of popcorn. Complete the table to show the number of times a large popcorn without butter was sold.
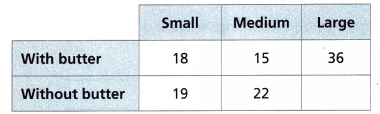
Answer:
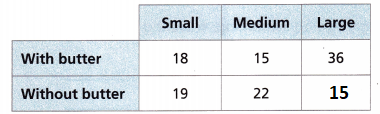
The number of popcorns is 18 + 15 + 36 + 19 + 22 + x = 125
= 110 + x = 125
= 125 – 110 = x
x = 15
The popcorn without butter is 15.
B. Find the experimental probability of a new customer ordering a large popcorn without butter.
Answer:
The large popcorn without butter = 15
The total number of popcorns = 125
The experimental probability of the popcorn without butter = number of events occurring/ total number of trials = 15/125 = 3/25.
Question 5.
Construct Arguments When simulating a compound event by rolling a number cube and flipping a coin, does it matter which one is done first? Explain your answer.
Answer:
The table shows activities chosen. For Problems 6-9, use the table to determine the experimental probability of the choice and its complement.
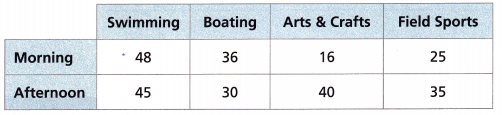
Question 6.
swimming in the afternoon _______________
Answer:
Question 7.
field sports in the morning _______________
Answer:
Question 8.
boating in the morning _______________
Answer:
Question 9.
arts & crafts in the afternoon _______________
Answer:
Use Tools For Problems 10-12, tell how you could use the tools shown to simulate each compound event.
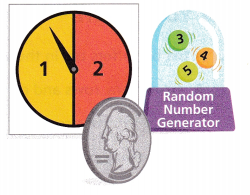
Question 10.
Choosing a pet at the animal shelter: a male or female; a cat, a dog, or a rabbit
Answer:
Question 11.
Choosing colors for a shed: a red, blue, or yellow shed with white, gray, or black trim
Answer:
Question 12.
Choosing an activity: going hiking or going swimming; traveling by bus or traveling by bicycle
Answer:
Question 13.
Open-Ended Write a word problem that includes finding the possible outcomes, and the size of the sample space, for a compound event. Then find the size of the sample space described in your problem.
Answer:
I’m in a Learning Mindset!
If you want to adjust the level of challenge in a simulation, would changing the order of simple events work? Why or why not?
Answer:
Lesson 14.3 More Practice/Homework
Question 1.
Math on the Spot A compound event is simulated by flipping a coin (H or T) and rolling a number cube (1—6).
A. List all the different possible outcomes.
Answer:
The possible outcomes is (1, H), (2, H), (3, H), (4, H), (5, H), (6, H).
(1, T), (2,T), (3,T), (4, T), (5,T), (6,7).
B. Represent the sample space using the table.

Answer:
The possible outcomes is (1, H), (2, H), (3, H), (4, H), (5, H), (6, H).
(1, T), (2,T), (3,T), (4, T), (5,T), (6,7).

Model with Mathematics Nico rolled two number cubes 250 times. The table shows his results. Use the table for Problems 2-4.
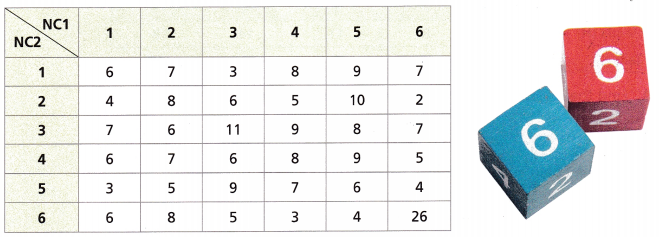
Question 2.
Find the experimental probability of rolling a 5 on the first number cube and a 2 on the second number cube.
Answer:
The experimental probability of rolling a 5 on the first number cube = 1/6
The experimental probability of rolling a 2 on the second number cube = 1/6.
The experimental probability of rolling a 5 on the first number cube and a 2 on the second number cube = 1/6 x 1/6 = 1/36.
Question 3.
A. Find the experimental probability of rolling a 1 on the second number cube.
Answer:
The experimental probability = number of events occurring/ total number of trials
The experimental probability of rolling a 1 on the second number cube = 1/6.
B. Use the complement to find the experimental probability of NOT rolling a 1 on the second number cube.
Answer:
The experimental probability = number of events occurring/ total number of trials
The experimental probability of rolling a 1 on the second number cube = 1/6.
Question 4.
Reason Find the experimental probability of rolling double sixes. Is this experimental probability close to what you would expect? Explain.
Answer:
Test Prep
Question 5.
Carlotta is doing an experiment by flipping a coin and rollling a number cube. Select all that apply to the sample space of the experiment.
(A) The possible outcomes for the simulation can be represented in a table with 2 rows and 6 columns.
(B) The possible outcomes for the simulation can be represented in a table with 6 rows and 2 columns.
(C) The sample space of the simulation can only be represented by a table.
(D The sample space has 36 total possible outcomes.
(E) The sample space has 8 total possible outcomes.
Answer:
Question 6.
Ali runs a simulation using a coin and random number generator with output from 1 to 5. The table shows the results of the simulation.

A. Find the experimental probability of the outcome H-4.
Answer: H-4 = 14/14+7 = 14/21 = 2/3
B. Use the complement to find the experimental probability of NOT H-4.
Answer: The experimental probability of NOT H-4 = 1 – p
= 1 – 2/3
= 3-2/3 = 1/3
Spiral Review
Question 7.
John is using a number cube to simulate the outcome of rain or no rain with a 50% chance of rain forecast. Describe how he can interpret the outcome from each roll of the number cube to perform his simulation.
Answer:
Question 8.
Using a number or a number range, describe the probability of rolling a 3 on a number cube.
Answer:
The cube has 6 sides.
The experimental probability = number of events occurring/ total number of trials
The probability of rolling 3 on a number cube = 1/6
Question 9.
Describe the graph of a proportional relationship on a coordinate plane.
Answer: