We included HMH Into Math Grade 6 Answer Key PDF Module 9 Lesson 4 Use One-Step Equations to Solve a Variety of Problems to make students experts in learning maths.
HMH Into Math Grade 6 Module 9 Lesson 4 Answer Key Use One-Step Equations to Solve a Variety of Problems
I Can write and graph equations to solve a variety of real-world situations involving addition, subtraction, multiplication, or division.
Step it Out
Question 1.
The sum of the measures of the two angles shown is 180°. What is the unknown angle measure?
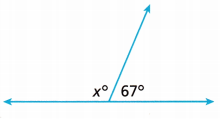
A. In the diagram, the unknown angle measure is labeled x°. What is the measure of the given angle?
Answer:
x° + 67° = 180°
x° = 180° – 67°
x° = 113°
B. Write an equation to represent the relationship in the diagram.
![]() +
+ ![]() = 180
= 180
Answer: x° + 67° = 180°
C. Solve the equation using the Subtraction Property of Equality.
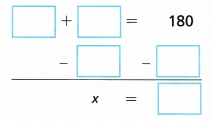
Answer:
x° + 67° = 180°
x° = 180° – 67°
x° = 113°
D. The unknown angle measure is ![]() .
.
Answer:
The unknown angle measure is 113°.
Question 2.
A store sells 3 cell phone cases for the price shown. Write and solve an equation to find how much money x the store charges for each case.

A. Write an equation to represent this situation.
![]() x = $
x = $ ![]()
Answer:
A store sells 3 cell phone cases for the price shown.
The cost of 3 cell phones is $50.25
The equation would be
3x = $50.25
B. Solve the equation using the Division Property of Equality. What does x represent?
Answer:
3x = $50.25
x = 50.25/3
x = $16.75
The cost of 1 cell phone is $16.75
Turn and Talk The sum of the measures of two angles is 90°. If the angles have the same measure, what is the measure of each angle? Explain.
Answer:
The sum of the measures of two angles is 90°
x° + x° = 90°
2x° = 90
x° = 90/2
x° = 45°
Thus the measure of each angle is 45°.
Question 3.
Paul has his laptop open at a 105° angle. If he closes his laptop to a 19° angle or less, the laptop will go into sleep mode. How many degrees x does Paul need to close his laptop before it will go into sleep mode?
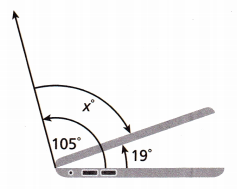
A. Write an equation you can use to solve for the unknown angle measure.
x + ![]() =
= ![]()
Answer:
x + 19 = 105
B. Solve the equation using the Subtraction Property of Equality.
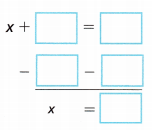
Answer:
x + 19 = 105
x = 105 – 19
x = 86
C. The measure of the unknown angle is ![]() .
.
Answer: The measure of the unknown angle is 86 degrees.
Question 4.
The picture shows the flat and angled positions that an artist likes her tablet in when drawing. The flat viewing angle measures 180°. What is the measure of the unknown angle?
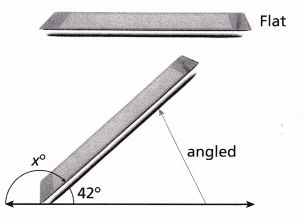
A. Write an equation you can use to find the second viewing angle.
![]() + x =
+ x = ![]()
Answer:
The flat viewing angle measures 180°.
42 + x = 180
B. Solve the equation.
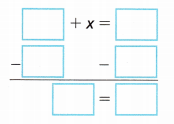
Answer:
42 + x = 180
x = 180 – 42
x = 138 degrees
C. The measure of the unknown angle is ![]() .
.
Answer: The measure of the unknown angle is 138.
Check Understanding
Question 1.
The perimeter of a square is 68 inches. Write and solve an equation to find the length of its sides.
Answer:
Given,
The perimeter of a square is 68 inches.
We know that,
The perimeter of a square = 4s
68 = 4s
s = 68/4
s = 17 inches
Thus the length of its side is 17 inches.
Question 2.
Kamal makes $12.00 an hour at his job. Last week he earned $390. Write and solve an equation to determine how many hours Kamal worked last week.
Answer:
Given,
Kamal makes $12.00 an hour at his job. Last week he earned $390.
x × 12 = 390
x = 390/12
x = 32.5
Thus Kamal worked 32.5 hours last week.
On Your Own
Question 3.
Model with Mathematics In a pack of pretzel sticks, one- quarter of the total number of pretzel sticks is 14. Write and solve an equation to find the total number of pretzel sticks in the pack x.

Answer:
Given,
In a pack of pretzel sticks, one- quarter of the total number of pretzel sticks is 14.
1/4 × x = 14
x = 14 × 4
x = 56
Thus the total number of pretzel sticks in the pack x is 56.
Question 4.
The sum of Ryan’s age and Rene’s age is 35. If Ryan is 16 years old, how old is Rene?
A. Let x represent Rene’s age. Write and solve an equation for x.
Answer:
Given,
The sum of Ryan’s age and Rene’s age is 35.
Ryan is 16 years old
x + 16 = 35
B. How old is Rene?
Answer:
x + 16 = 35
x = 35 – 16
x = 19
Thus Rene’s age is 19 years.
Question 5.
The triangular-shaped walking path in the park shown has a perimeter of 990 feet.
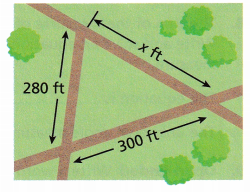
A. Write an equation to find the length of the side of the path represented by x.
Answer:
The triangular-shaped walking path in the park shown has a perimeter of 990 feet.
a = 280 ft
b = 300 ft
Perimeter is the sum of all sides.
280 + 300 + x = 990
x + 580 = 990
x = 990 – 580
x = 410
B. Solve the equation. How long is the third side of the path? Show your work.
Answer:
280 + 300 + x = 990
x + 580 = 990
x = 990 – 580
x = 410
Thus the third side of the path is 410 ft.
Question 6.
A box is in the shape of a right rectangular prism. The area of one of the bases is shown. What is the height h of the box? Use the formula V = B × h, where V is the volume of the right rectangular prism, B is the area of the base, and h is the height.
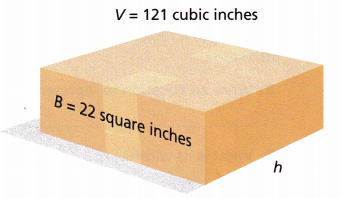
Answer:
Given,
A box is in the shape of a right rectangular prism. The area of one of the bases is shown.
Use the formula V = B × h,
where V is the volume of the right rectangular prism,
B is the area of the base, and h is the height.
V = 121 cubic inches
B = 22 sq. inches
121 = 22 × h
h = 121/22
h = 5.5 inches
Question 7.
The formula for the area A of a rectangle is A = l × w. The formula for the perimeter P of a rectangle is P = 2l + 2w. The area of the front of a rectangular window flower box is shown.

A. What is the length of the flower box?
Answer:
The formula for the area A of a rectangle is A = l × w.
A = 10 1/2 sq. in
W = 2 1/4 in.
A = l × w.
10 1/2 = l × 2 1/4
21/2 ÷ 9/4 = l
l = 84/18 = 4 2/3 in.
Thus the length is 4 2/3 inches.
B. What is the perimeter of the front of the flower box?
Answer:
The formula for the perimeter P of a rectangle is P = 2l + 2w.
P = 2(84/18 + 9/4)
P = 84/9 + 9/2
P = 13 5/6 inches
Thus the perimeter of the rectangle is 13 5/6 inches.
Question 8.
The sum of the measures of the two angles shown is 180°. Write and solve an equation to find the unknown angle measure.
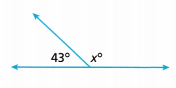
The equation is ___________
The unknown angle measure is ____________
Answer:
The sum of the measures of the two angles shown is 180°.
x° + 43° = 180°
x° = 180° – 43°
x° = 137°
Thus the unknown angle is 137°.
Question 9.
Open-Ended Write a word problem for the equation x – 6 = 20.
Answer:
If 6 is subtracted from the unknown number x then the difference is 20.
x – 6 = 20
x = 20 + 6
x = 26
Question 10.
Five pounds of cherries cost $14.95. Write and solve an equation to determine how much each pound of cherries costs.
Answer:
Given,
Five pounds of cherries cost $14.95.
5x = 14.95
We need to write and solve an equation to determine how much each pound of cherries costs.
5x = 14.95
x = 14.95/5
x = 2.99
Thus the cost of each pound of cherries is $2.99
Question 11.
Sophie buys milk and vegetables at the grocery store. She spends $3.29 on milk and has a total bill of $15.56. Write and solve an equation to determine how much Sophie spends on the vegetables.
Answer:
Given,
Sophie buys milk and vegetables at the grocery store.
She spends $3.29 on milk and has a total bill of $15.56.
x + 3.29 = 15.56
x = 15.56 – 3.29
x = 12.27
Thus Sohpie spends $12.27 on the vegetables.
Question 12.
The area of a rectangle is 36 square inches. Its length is 9 inches. What is its width?
A. Write an equation to represent this situation. Let w represent the width.
Answer:
Given,
The area of a rectangle is 36 square inches.
Its length is 9 inches.
width = x
Area of a rectangle = l × w
36 = 9 × x
x = 36/9
x = 4
Thus the width is 4 inches.
B. What is its width?
Answer:
The width is 4 inches.
Lesson 9.4 More Practice/Homework
Question 1.
The two angles at the right have a combined measure of 90°. Write and solve an equation to find the measure of angle x. Show your work.
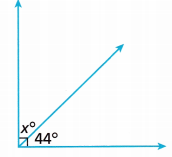
Answer:
Given,
The two angles at the right have a combined measure of 90°.
The unknown angle is x degrees.
x° + 44° = 90°
x° = 90° – 44°
x° = 46°
Question 2.
Janelle weighed an unknown substance. It had a mass of 20.609 grams. She exposed the substance to a flame and carefully weighed the substance again. The substance then had a mass of 17.39 grams. Write and solve an equation to determine the amount of mass x the substance lost.

Answer:
Given,
Janelle weighed an unknown substance. It had a mass of 20.609 grams.
She exposed the substance to a flame and carefully weighed the substance again.
The substance then had a mass of 17.39 grams.
The equation would be
x – 17.39 = 20.609
x = 20.609 + 17.39
x = 37.999 or 38 approx.
Question 3.
Model with Mathematics Rosario is working on an 8-foot-by- 8-foot floor covered with 64 white tiles. She replaces x white tiles with blue tiles. After she’s finished, there are 40 white tiles left. Write and solve an equation to find the number of blue floor tiles Rosario used.
Rosario used __________ blue tiles.
Answer:
Rosario is working on an 8-foot-by- 8-foot floor covered with 64 white tiles.
She replaces x white tiles with blue tiles.
After she’s finished, there are 4.0 white tiles left.
The equation would be y = 64 – x
Now after she’s finished the work, there are 40 white tiles left.
y = 40
40 = 64 – x
x = 64 – 40
x = 24
Hence the number of blue tiles is 24.
Question 4.
Math on the Spot The distance between Professor Burger’s house and Chris’ house is 12 miles. Lila’s house is on the way from Professor Burger’s house to Chris’ house. The distance between Lila’s house and Chris’ house is 5 miles. Write and solve an equation to find the distance x between Professor Burger’s house and Lila’s house.
Answer:
Given,
The distance between Professor Burger’s house and Chris’ house is 12 miles.
Lila’s house is on the way from Professor Burger’s house to Chris’ house.
The distance between Lila’s house and Chris’ house is 5 miles.
x + 5 = 12
x = 12 – 5
x = 7
Thus the distance between Professor Burger’s house and Lila’s house is 7 miles.
Question 5.
Model with Mathematics A store had a sale on baseball cards, so Percy bought several baseball cards to give as gifts. He gave a total of x baseball cards away to 5 friends. Each friend got 4 baseball cards. Write and solve an equation to figure out how many baseball cards Percy gave away.
Answer:
Given,
A store had a sale on baseball cards, so Percy bought several baseball cards to give as gifts.
He gave a total of x baseball cards away to 5 friends. Each friend got 4 baseball cards.
x/5 = 4
x = 5 × 4
x = 20
Thus Percy gave away 20 baseball cards.
Test Prep
Question 6.
A swinging door opens to form a 90° angle. If the door is swung 36° closed, how many more degrees can the door close?
Answer:
Given,
A swinging door opens to form a 90° angle.
If the door is swung 36° closed.
x + 36 = 90
x = 90 – 36
x = 54°
The door can close at 54 degrees.
Question 7.
The area of a rectangle is 120 square inches. Its length is 15 inches. Write an equation to find its width. What is its width?
Answer:
Given,
The area of a rectangle is 120 square inches. Its length is 15 inches.
The equation to find width would be
x × 15 = 120
x = 120/15
x = 8
Thus the width is 8 inches.
Question 8.
Ginger withdrew $220 from her bank account. After her withdrawal, there was $345 left in her account. Write and solve an equation to find how much Ginger had in her account before the withdrawal.
Answer:
Given,
Ginger withdrew $220 from her bank account. After her withdrawal, there was $345 left in her account.
x – 220 = 345
x = 345 + 220
x = 565
Therefore Ginger has $565 in her account before the withdrawal.
Question 9.
The perimeter P of the triangle is equal to the sum of the lengths of the three sides. The perimeter is 194.2 centimeters. Find the value of b.
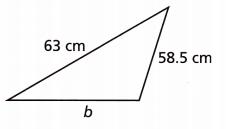
b = ____________
Answer:
The perimeter P of the triangle is equal to the sum of the lengths of the three sides.
The perimeter is 194.2 centimeters.
63 + 58.5 + b = 194.2 cm
121.5 + b = 194.2 cm
b = 194.2 – 121.5
b = 72.7 cm
Thus the value of b is 72.7 cm.
Question 10.
The sum of the measures of two angles is 90°. One angle has a measure of 32.8°. The measure of the other angle is represented by x. What is the value of x?
x = __________
Answer:
Given,
The sum of the measures of two angles is 90°.
One angle has a measure of 32.8°.
The measure of the other angle is represented by x.
The equation would be
x + 32.8 = 90
x = 90 – 32.8
x = 57.2°
Thus the value of x is 57.2°
Spiral Review
Question 11.
Plot the following integers on the number line: -4, 6, -2, 5, -8.

Answer:
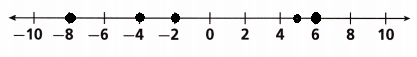
The integer 0 is marked on the number line and positive integers on the right side from 0 and negative integers from the left side.
-4 is marked on the number line from the left side of 0.
6 is marked on the number line from the right side of 0.
-2 is marked on the number line from the left side of 0.
5 is marked on the number line from the right side of 0.
-8 is marked on the number line from the left side of 0.
Question 12.
A relay race covers a distance of 2\(\frac{1}{2}\) miles. Each runner on the team will run \(\frac{1}{4}\) mile. How many runners are needed for the team to cover the total distance of the race?
Answer:
Given,
A relay race covers a distance of 2\(\frac{1}{2}\) miles.
Each runner on the team will run \(\frac{1}{4}\) mile.
We need to find how many runners are needed for a team.
Let the required number be x.
\(\frac{1}{4}\) x = 2\(\frac{1}{2}\)
\(\frac{1}{4}\) x = \(\frac{5}{2}\)
x = 20/2
x = 10
Thus the number of runners needed for a team is 10.