Into Math Grade 6 Module 9 Lesson 5 Answer Key Write and Graph Inequalities

We included HMH Into Math Grade 6 Answer Key PDF Module 9 Lesson 5 Write and Graph Inequalities to make students experts in learning maths.

HMH Into Math Grade 6 Module 9 Lesson 5 Answer Key Write and Graph Inequalities

I Can write and graph the solution of an inequality to represent a condition in a real-world or mathematical problem.

Step It Out

You can write inequalities using inequality symbols and variables to describe quantities that have many values.
Connect to Vocabulary
An Inequality is a mathematical sentence that shows the relationship between quantities that are not equal.

Question 1.
A record-breaking low temperature of -23 °F was recorded in Seminole, Texas, on February 8, 1933.

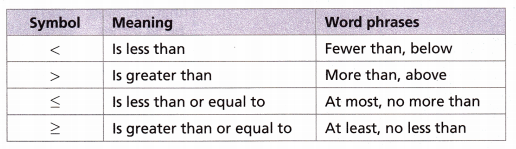
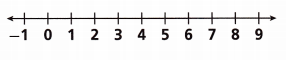
A. Find -23 and graph it on the number line.

Answer:

B. The temperatures 4 °F, -3 °F, -14 °F, 1 °F, and -19 °F have also been recorded in Texas. How do these temperatures compare to -23 °F?
Answer:
Given that,
The temperatures recorded in Texas is 4 °F, -3 °F, -14 °F, 1 °F, and -19 °F.
Comparing the above temperature with -23 °F.
-23 °F<4 °F, -3 °F, -14 °F, 1 °F, and -19 °F.

C. Give examples of other numbers that are greater than -23. How many of these numbers exist?
Answer:
The other numbers greater than -23 is -22, -20, -18, -16, -14, -12, -10, -8, -6, -4, -2. 0, 2, 4.
There are14 numbers that can exist.

D. Let x represent the temperatures greater than -23 °F. Complete the inequality to describe these temperatures.
x -23
Answer:
Given that x represents the temperature.
The temperature is greater than the -23.
The inequality to describe these temperatures is x > -23.

Turn and Talk How is a number line not like a thermometer? Explain.
Answer:

The solution of the inequality x > 2 is all numbers greater than 2, not including 2.

Connect to Vocabulary
The solution of an Inequality is a value or values that make an inequality true. An inequality can have many solutions.

An inequality such as x > 2 represents a constraint. A constraint is a condition that restricts the values of a quantity or variable to a given value or range of values. For the inequality x > 2, the values of x must be greater than 2. So, 2 and numbers less than 2 are not solutions of x > 2.

For the inequality x ≤ 4, the values of x must be less than or equal to 4. So, 4 is a solution of x ≤ 4, but numbers greater than 4 are not solutions.

Question 2.
Graph the inequalities.
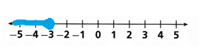
A. y ≤ -3
Step 1: Draw a solid circle at -3 to show that -3 is a solution.

Step 2: Shade the number line to the left of -3 to show that numbers less than -3 are also solutions.
Step 3: Check your solution. Choose a number that is on the shaded section of the number line, such as -4. Substitute -4 for y. Since the inequality -4 ≤ -3 is true, the solution graphed on the number line appears to be correct. You can never check all the possible values for the variable but checking one or two values helps assure you have shaded the correct side of the number line.
Answer:
Given that,
The equation is y ≤ -3
For the inequality x ≤ -3, the values of x must be less than or equal to -3. So, -3 is a solution of x ≤ -3, but numbers greater than -3 are not solutions.

The shaded circle on the -3 indicates that -3 is a solution of x ≤ -3.
-4 ≤ -3 is true, the solution on the number line appears correct.
The other value is -5.
-5 ≤ -3 is true, the solution on the number line appears correct.

B. 1 < m

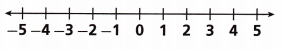
Step 1: Draw an open circle at 1 to show that 1 is not a solution.
Step 2: Shade the number line to the right of 1 to show that numbers greater than 1 are solutions.
Step 3: Check your solution. Pick any number for m that falls on the shaded section of the number line. 1 < . If the inequality you have just written is true, then you have shaded the correct side of the number line.
Answer:
Given that the equation is 1 < m.

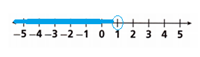
The circle is drawn on the 1 it indicates that 1 is not a solution.
The shaded line shows that the numbers greater than 1 are the solutions.
Let us consider m = 0.
1 < 0
It shows the shaded part is the correct side of the number line.

Turn and Talk Think of a situation you have faced where something must be greater than a certain amount. Think of a second situation where something must be greater than or equal to a certain amount. Explain each scenario and then write an inequality to represent each situation.

You can write inequalities to represent certain real-world situations.

Question 3.
Use inequalities to solve these problems.
A. The temperature is at most -2 °F. What could be the temperature f?
Are numbers less than -2 part of the solution?
Are numbers greater than -2 part of the solution?
Is -2 included as a solution?
Write the inequality, t -2
Answer:
Given that,
The temperature is at most -2 °F.
It means the temperature t is less than or equal -2.
The inequality equation is t ≤ -2
The -2 is included in the solution.

B. Raphael needs to buy more than 4 concert tickets. How many tickets t could he buy?

Are numbers less than 4 part of the solution?
Are numbers greater than 4 part of the solution?
Is 4 included as a solution? _____
Write the inequality, t 4
Graph the inequality. Use an open circle because the value 4 is not part of the solution.

Answer:
Given that,
Raphael needs to buy more than 4 concert tickets.
It means the tickets t is greater than 4.
The inequality equation is t > 4.
The number 4 is not included in the solution.

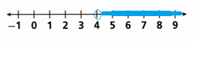
The circle indicates that the number 4 is not the solution.
The shaded part shows the solution.

Check Understanding

Question 1.
Camille wants to become a pilot. A pilot needs to log at least 500 flying hours before earning a pilot’s license. Write and graph an inequality to show the number of flying hours h Camille needs to get a license.

Answer:
Given that,
A pilot needs to log at least 500 flying hours before earning a pilot’s license.
The number of flying hours = h
The inequality equation is h ≥ 500

The shaded circle indicates the solution includes the 500.
The shaded part is the solution.

For Problems 2-3, graph each inequality.

Question 2.
r ≤ 8

Answer:
Given that,
The inequality equation is r ≤ 8.

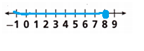
The shaded circle indicates the number 8 is included in the solution.
The shaded part is the solution.

Question 3.
z < -3

Answer:
Given that,
The inequality equation is z < -3.

The circle indicates the number -3 is not included in the solution.
The shaded part is the solution.

On Your Own

Question 4.
When cooking chicken, the recommended internal temperature of the chicken is shown. A lower internal temperature will undercook the chicken. Write an inequality to describe the temperatures t at which the chicken will be undercooked.
Graph the inequality.

Answer:
Given that,
Inequality to describe the temperatures t at which the chicken will be undercooked is t < 165°F

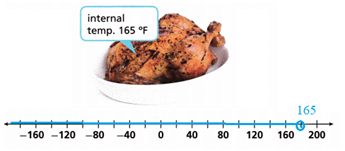
The circle shows that the solution is not included the 165°F.
The shaded part is the solution.

Question 5.
STEM The speed of sound is approximately 761 miles per hour. For an object to produce a sonic boom, it must travel faster than the speed of sound. Write an inequality to describe the speeds s at which a moving object will produce a sonic boom.
Answer:
Given,
The speed of sound is approximately 761 miles per hour.
For an object to produce a sonic boom, it must travel faster than the speed of sound.
s is faster than 761 miles.
Thus the inequality is s > 761.

Question 6.
To find the area A of a rectangle, the length l must be multiplied by the width w. A farmer needs to build a fence to enclose a chicken pen with an area greater than or equal to 50 square feet. The length of the fence must be 10 feet.

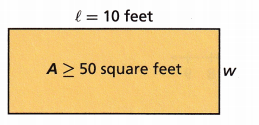
A. Write an inequality to describe the widths w that will yield a fenced-in area of at least 50 square feet.
Answer:
Let A = 50
l = 10
Area = l × w
50 = 10 × w
w = 50/10 = 5
Thus w > 5

B. Graph the inequality.

Answer:
Put a closed point on the number 5 running to the right.

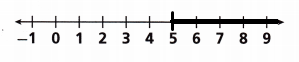
Question 7.
The temperature in Minneapolis was -9 °F. The next day, the temperature in Minneapolis was warmer than -9 °F.
A. Write an inequality which is true only for temperatures t that are warmer than -9 °F.
Answer:
The temperature in Minneapolis was -9 °F.
The next day, the temperature in Minneapolis was warmer than -9 °F.
-9 °F < t

B. Could the temperature have been -12 °F in Minneapolis on the next day? Why or why not?
Answer:

Question 8.
A. Graph the inequality d ≤ -2

Answer:

B. Reason Name three solutions for d. How many possible solutions does this inequality have?
Answer:
d = -2
d < -2
d ≤ -2

Question 9.
Write an inequality to represent the graph. Use y for the solution.

Answer: y ≥ -4.

Question 10.
To have enough orange juice for all the campers, the camp cook will need at least 9 gallons.
A. Write an inequality that is true only for the number of gallons g the cook needs.
Answer:
As per the given question, the inequality is g ≥ 9.

B. Graph the inequality.

Answer:

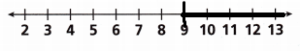
C. If the cook buys 4 gallons, will there be enough orange juice?
Answer:

Question 11.
According to government guidelines, drones are limited to how high they can legally fly above the ground as shown.

A. Write an inequality that is true only for the height h a drone can fly above the ground.
Answer: d ≤ 400

B. If a drone flies 430 feet above the ground, will it violate government guidelines? Explain.
Answer: Yes, the actual limit is 400 feet.
The inequality is d is less than or equal to 400.
Thus If a drone flies 430 feet above the ground it will violate the government guidelines.

Question 12.
Write an inequality that represents the graph. Use x for the variable.

Answer: x < 1

Question 13.
A. Write an inequality that represents the graph. Use x for the variable.

Answer: x ≥ 90

B. Choose a number from the shaded area of the graph to check your inequality. State the number you picked and explain why it is a possible solution.
Answer: The possible solution might be x ≥ 90

Question 14.
Graph the inequality on the number line: b ≥ -14.

Answer:

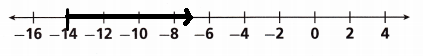
The symbols mean that a number is strictly less than or greater than another number.
Locate -14 on the number line and draw a line from -14 to the right side of the number line.

Question 15.
Graph the inequality on the number line: d < 25.

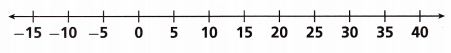
Answer:

First plot the point 25 on the number line.
Now draw the line from 25 to the left side of the number line.

Question 16.
A dog weighs less than 15 pounds.

A. List three possible weights for the dog.
Answer:
The three possible weighs for the dog are 14, 13 and 12.

B. Write an inequality that describes the possible weights w the dog can weigh.
Answer: x < 15 < 14< 13<12.

C. Some puppies can be born with a weight of \(\frac{1}{5}\) of a pound. Can any dog ever weigh 0 pounds or less?
Answer:
Some puppies can be born with a weight of \(\frac{1}{5}\) of a pound.
The weight of the dog cannot be 0 or less than 0.

D. An inequality can be written with a variable between two numbers if that variable must be greater than one number and less than another number. Write a new, more accurate inequality to describe the dog’s possible weight by writing an inequality symbol in each blank.
0 w 15
Answer:
The inequality is 0 > w < 15

E. Graph this new inequality.

Answer:

Question 17.
Open-Ended Write a situation that can be modeled by x < 7.
Answer:
x < 7
So it means that x is lower than 7 like if you draw a number line x<6 x<5 x<4 and so on

Lesson 9.5 More Practice/Homework

Question 1.
Regan won the grand prize at a store giveaway. The grand prize winner is guaranteed to win at least $500 in cash and prizes.
A. List three possible dollar amounts in cash and prizes Regan can win.
Answer:
Inequality is an expression used to show the relationship between two or more numbers and variables.
Let d represent the amount of cash in dollars and p represents the number of prizes.

B. Write an inequality to represent the dollar amounts d in cash and prizes Regan can win.
Answer:
Since the grand prize winner is guaranteed to win at least $500.
p + d ≥ 500

C. Graph the inequality.

Answer:

Question 2.
STEM Alonso uses the table to help him identify an unknown mineral. He finds the specific gravity of the mineral and discovers it is less than 3.

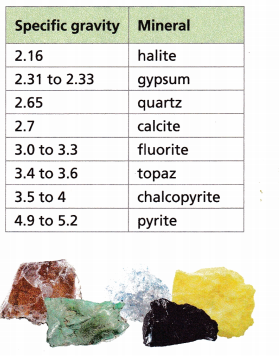
A. List three possible minerals the unknown mineral could be.
Answer:
The minerals specific gravity is less than 3.
Minerals less than 3 are
Halite – 2.16
Gypsum – 2.31 to 2.33
Quartz – 2.65
Calcite – 2.7

B. Write an inequality to represent the specific gravity g of the unknown mineral.
Answer:
Gravity g of the unknown mineral is g < 3.

Math on the Spot For Problems 3-4, graph each inequality on a number line.

Question 3.
x > -7

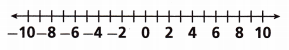
Answer:

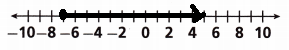
Plot -7 on the number line.
Now draw a line from -7 to the right side.
This indicates that -7 is greater than -7.

Question 4.
y ≤ -5

Answer:

First plot the point on -5 on the number line.
Now draw the line from -5 to the left.

Question 5.
Reason When two numbers are added together, the sum is at least 100. One of the numbers is 77.
A. Which of these could be the other number? Circle the correct number or numbers.
15    9     23      41      50      20      25
Answer:
77 + 23 = 100
So, 23 could be the other number.

B. Write an inequality to represent the possible values of the other number n.
Answer:
We know that adding two numbers (77 and n) must be ≥ 100.
77 + n ≥ 100

Test Prep

Question 6.
Children 12 and under eat free at a local restaurant. If x represents age, write an inequality to represent the ages of people who do not get a discount.
Answer:
Kids 12 and under, meaning that the age of someone who enters the restaurant has to be less than or equal to 12 to eat free.
12 ≤ x

Question 7.
It is colder than -7 °F outside. Which inequality represents the temperature t?
(A) 7 < t
(B) t > -7
(C) -7 > t
(D) t < 7
Answer:
If the temperature is lower than -7 degrees Fahrenheit, then the inequality must show a number less than -7.
Or in other words, -7 is greater than what the temperature is, thus the answer is -7>t
Option C is the correct answer.

Question 8.
An online retailer charges an additional fee to ship orders that weigh over 48 pounds. Write and graph an inequality which represents the weight x of online orders that result in an additional fee.

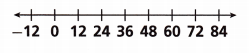
Answer:
Given,
An online retailer charges an additional fee to ship orders that weigh over 48 pounds.
The inequality is x > 48, the graph is shown below

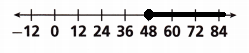
Question 9.
Draw a line to match each graph with the inequality that it represents.

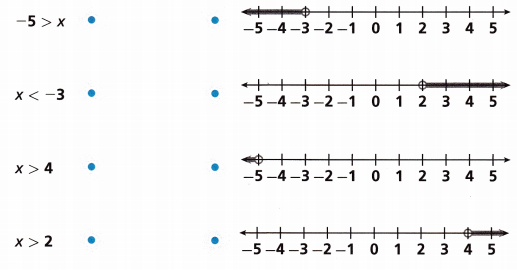
Answer:

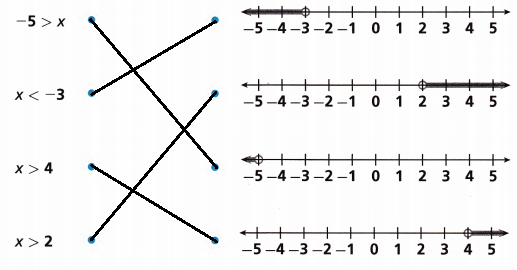
Explanation:
-5 > x: Plot the point on -5 and draw the line to the left from -5.
x < -3: Plot the point on -3 and draw the line to the left from -3.
x > 4: Plot the point on 4 and draw the line to the right from 4.
x > 2: Plot the point on 2 and draw the line to the right from 2.

Spiral Review

Question 10.
Benjamin bought 4 goldfish. Each goldfish cost $1.29. How much did Benjamin spend?
Answer:
Given,
Benjamin bought 4 goldfish.
Each goldfish cost $1.29.
1.29 × 4 = 5.16
Therefore Benjamin spends $5.16 on goldfish.

Question 11.
A youth league soccer team has 20 students who play defender positions and 23 students who play midfielder positions. Write a ratio of students who play defender positions to the total number of students who play defender or midfielder positions.
Answer:
Given,
A youth league soccer team has 20 students who play defender positions and 23 students who play midfielder positions.
Total number of students = 20 + 23 = 43
The ratio of students who play defender positions to the total number of students who play defender or midfielder positions = 20 : 43

For Problems 12-15. find each quotient or product.

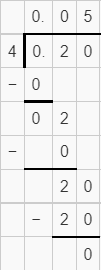
Question 12.
0.2 ÷ 4
Answer: 0.05

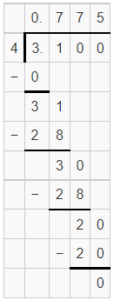
Question 13.
3.1 ÷ 4
Answer: 0.775

Question 14.
0.2 × 0.25
Answer: 0.05
There’s 3 total decimal places in both numbers.
Ignore the decimal places and complete the multiplication as if operating on two integers.
2 × 25 = 50
Rewrite the product with 3 total decimal places.
0.2 × 0.25 = 0.050

Question 15.
3.1 × 0.25
Answer: 0.775
There’s 3 total decimal places in both numbers.
Ignore the decimal places and complete the multiplication as if operating on two integers.
31 × 25 = 775
3.1 × 0.25 = 0.775