We included HMH Into Math Grade 6 Answer Key PDF Module 9 Lesson 3 Use Multiplication and Division Equations to Solve Problems to make students experts in learning maths.
HMH Into Math Grade 6 Module 9 Lesson 3 Answer Key Use Multiplication and Division Equations to Solve Problems
I Can write and solve equations using multiplication and division to represent real-world situations involving an unknown.
Spark Your Learning
Diana is preparing lunch for her friends. She has 0.75 pound of ham and 0.5 pound of cheese. She uses 0.15 pound of ham and 0.08 pound of cheese to make a ham and cheese sandwich. Is there enough ham and cheese to make 5 sandwiches if she uses the same amount of ham and cheese for each sandwich? Explain.

Answer:
Given,
Diana is preparing lunch for her friends. She has 0.75 pound of ham and 0.5 pound of cheese.
Total = 0.75 + 0.50 = 1.25 pound of ham and cheese
She uses 0.15 pound of ham and 0.08 pound of cheese to make a ham and cheese sandwich.
0.15 + 0.08 = 0.23 pound of ham and cheese to make each sandwich
0.23 × 5 = 1.15
1.15 is 1.25
So, it is enough to make 5 sandwiches.
Turn and Talk If ham costs $5.79 per pound and cheese costs $4.29 per pound, how can you find the total amount you pay for the ham and cheese in each sandwich? Can you stay within a budget of $1.50 per sandwich? Explain.
Answer:
ham costs $5.79 per pound and cheese costs $4.29 per pound
5.79 + 4.29 = 10.08
We need to add the price to find the total amount you pay for the ham and cheese in each sandwich.
0.15 × 5.79 = 0.86
0.08 × 4.29 = 0.34
0.86 + 0.34 = 1.2
Yes, You stay within a budget of $1.50 because it costs $1.20 to make a sandwich.
Build Understanding
In the previous lesson, you learned to solve addition equations with a variable by subtracting. How can you solve a multiplication equation?
Question 1.
A group of 4 people goes apple picking. They pick the amount shown. If they share the apples equally, how many pounds of apples does each person get? Let x represent the weight in pounds of apples that each person receives.

A. Complete the diagram.
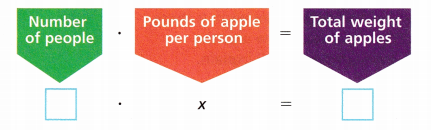
Answer:
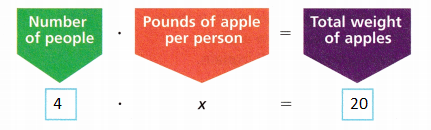
B. Write an equation to represent this problem.
Answer:
4x = 20
C. Model the equation using algebra tiles. How many x-tiles are in your model? How many 1-tiles?
Answer:
4x = 20
x = 20/4
x = 5
D. How many equal groups do you need to divide your model into to solve for x? Explain.
Answer: You need to divide by 4 to get equal groups of apples.
E. Draw circles around the tiles you drew for Part C to separate the tiles into equal groups.
Answer:
F. How many 1-tiles are in each group? How many pounds of apples does each person get?
Answer:
Turn and Talk What other method can you use to find how many pounds of apples each person gets? Explain.
Step It Out
The Division Property of Equality states that you can divide both sides of an equation by the same nonzero number and the two sides will remain equal.
Question 2.
What is the value of x in the equation 7x = 119?
A. Divide both sides of the equation by the same nonzero number to get x alone on one side.
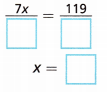
Answer:
7x = 119
x = 119/7
x = 17
B. To check the solution, substitute your answer in the original equation.
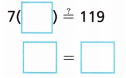
Does your solution check?
Answer:
x = 17
7 × 17 = 119
119 = 119
Our solution is correct.
The Multiplication Property of Equality states that you can multiply both sides of an equation by the same number and the two sides will remain equal.
Question 3.
What is the value of x in the equation \(\frac{x}{6}\) = 9?
A. Multiply both sides of the equation by the same number to get x
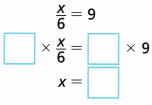
Answer:
\(\frac{x}{6}\) = 9
x = 9 × 6
x = 54
B. To check the solution, substitute your answer in the original equation.
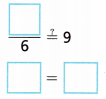
Does your solution check?
Answer:
x = 54
54/6 = 9
9 = 9
Our solution is correct.
C. Find the value of x if you know that \(\frac{x}{10}\) = 9. Describe how you found the solution.
Answer:
\(\frac{x}{10}\) = 9
x = 9 × 10
x = 90
Turn and Talk Why can’t you divide both sides of an equation by zero? Explain.
Answer:
We can’t divide both sides of an equation by zero. Because any number divided by 0 will be infinity.
Question 4.
A bag of 5 plum tomatoes weighs 1 pound. If each tomato weighs the same amount, what is the cost of one tomato? Use the equation 5x = 1.85.

A. To solve the equation 5x = 1.85, __________ both sides of the equation by the number ![]() .
.
Answer:
5x = 1.85
Divide both sides of the equation by the number 5.
x = 1.85/5
x = 0.37
B. The result of performing the same operation to both sides of the equation leads to the solution x = ![]() .
.
Answer:
x = 0.37
C. Graph your solution on the number line.
![]()
Answer:
![]()
D. To check the solution, put your answer into the original equation.
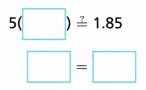
Does your solution check?
Answer:
5 × 0.37 = 1.85
1.85 = 1.85
Thus the solution is correct.
E. Interpret your answer.
Answer:
Turn and Talk How is solving a multiplication equation with decimals like solving a multiplication equation with whole numbers?
Answer:
Multiplying decimals is the same as multiplying whole numbers except for the placement of the decimal point in the answer. When you multiply decimals, the decimal point is placed in the product so that the number of decimal places in the product is the sum of the decimal places in the factors.
Check Understanding
Question 1.
Mr. Poyser uses 4\(\frac{2}{3}\) cups of flour to make 7 dozen oatmeal-raisin cookies. How many cups of flour does he need to make a dozen cookies? Use the equation 7c = 4\(\frac{2}{3}\). Graph the solution on a number line.

Answer:
Given,
Mr. Poyser uses 4\(\frac{2}{3}\) cups of flour to make 7 dozen oatmeal-raisin cookies.
Equation will be 7c = 4\(\frac{2}{3}\)
7c = \(\frac{14}{3}\)
c = \(\frac{14}{3}\) ÷ 7
c = 0.6

Question 2.
Four friends equally share the cost of lunch. Each person pays $14.00. How much is the total bill? Use the equation \(\frac{b}{4}\) = 14.
A. To find the total bill, I ___________ each side by ![]() .
.
Answer:
Given,
Four friends equally share the cost of lunch. Each person pays $14.00.
\(\frac{b}{4}\) = 14
b = 14 × 4
b = 56
B. b = ![]()
Answer:
b = 56
C. Graph the solution on a number line.

Answer:

On Your Own
Question 3.
Preston earns $33.00 for babysitting his neighbor’s children for 2.4 hours.
A. Model with Mathematics Write an equation you can use to find out how much Preston earns per hour.
Answer:
Given,
Preston earns $33.00 for babysitting his neighbor’s children for 2.4 hours.
x × 2.4 = 33
x = 33/2.4
x = 13.75
B. How much does Preston earn in one hour?
Answer: Preston earn $13.75 in one hour.
Question 4.
Henri has exactly enough quarters to wash 3 loads of laundry. It takes 8 quarters to wash one load of laundry. How many quarters does Henri have? Use the equation \(\frac{x}{3}\) = 8.
Answer:
Given,
Henri has exactly enough quarters to wash 3 loads of laundry.
It takes 8 quarters to wash one load of laundry.
By using the equation \(\frac{x}{3}\) = 8.
x = 8 × 3
x = 24
Henri have 24 quarters.
Question 5.
Use Tools Carlos has 6 mugs on a shelf as shown. The mugs all have the same weight. The equation 6x = 84 represents this situation.

A. What visual model could you use to solve the equation 6x = 84? Explain.
B. How much does each mug weigh?
Answer:
Given
Number of mugs = 6
Let each mug weigh will be x.
6x = 84
x = 84/6
x = 14
Thus the mug weighs 14 ounces.
For Problems 6-9, find each solution and graph it on the number line.
Question 6.
\(\frac{x}{3}\) = 4
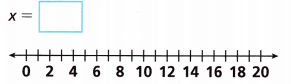
Answer:
\(\frac{x}{3}\) = 4
x = 4 × 3
x = 12
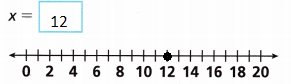
Question 7.
1.9x = 4.75
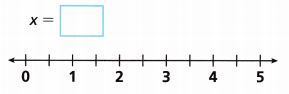
Answer:
1.9x = 4.75
x = 4.75/1.9
x = 2.5
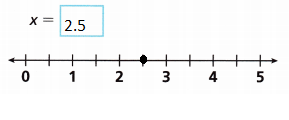
Question 8.
12x = 60

Answer:
12x = 60
x = 60/12
x = 5
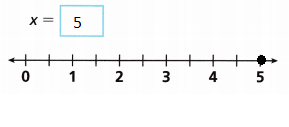
Question 9.
\(\frac{x}{5}\) = 3

Answer:
\(\frac{x}{5}\) = 3
x = 3 × 5
x = 15
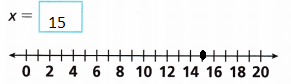
Question 10.
Glenn is 5 feet tall. He is \(\frac{4}{5}\) as tall as his brother. How tall is Glenn’s brother?
A. Model with Mathematics Write an equation to find Glenn’s brother’s height, using x to represent the height.
Answer:
Let the height of his brother be x.
\(\frac{4}{5}\)x = 5
B. How can you solve this equation for x?
Answer:
\(\frac{4}{5}\)x = 5
4x = 5 × 5
x = 25/4
x = 5 \(\frac{5}{4}\)
C. How tall is Glenn’s brother in feet?
Answer: Glenn’s brother is 5 \(\frac{5}{4}\) ft tall.
Question 11.
Iris made bracelets with string and beads. She used x centimeters of string and made 7 bracelets. She used 17.8 centimeters of string for each bracelet. How much string did she use in all? Write an equation and use it to solve this problem.
Answer:
Given,
Iris made bracelets with string and beads. She used x centimeters of string and made 7 bracelets. She used 17.8 centimeters of string for each bracelet.
The equation would be
x ÷ 17.8 = 7
x = 7 × 17.8
x = 124.6
Thus she use 124.6 centimeters in all.
Question 12.
Model with Mathematics The price of a can of beans is shown. Jason has $8.69 to spend on beans. Write an equation to represent the situation and solve the equation to find number of cans Jason can buy.

Answer:
The price of a can of beans is shown. Jason has $8.69 to spend on beans.
1 can = 0.79
x cans = 8.69
0.79x = 8.69
So, the equation is 0.79x = 8.69
x = 8.69/0.79
x = 11
Thus Jason can buy 11 cans of beans.
For Problems 13-16, find each solution.
Question 13.
9x = 171
Answer:
9x = 171
x = 171/9
x = 19
Question 14.
\(\frac{x}{6}\) = 15
Answer:
\(\frac{x}{6}\) = 15
x = 15 × 6
x = 90
Question 15.
\(\frac{9}{5}\)x = 2\(\frac{7}{10}\)
Answer:
\(\frac{9}{5}\)x = 2\(\frac{7}{10}\)
\(\frac{9}{5}\)x = \(\frac{27}{10}\)
x = \(\frac{27}{10}\) × \(\frac{5}{9}\)
x = \(\frac{3}{2}\) or 1 \(\frac{1}{2}\)
Question 16.
\(\frac{x}{4}\) = 28.80
Answer:
\(\frac{x}{4}\) = 28.80
x = 28.80 × 4
x = 115.2
I’m in a Learning Mindset!
How can I help a classmate develop a growth-mindset response?
Answer:
Lesson 9.3 More Practice/Homework
Question 1.
Model with Mathematics Selena buys 4 peaches that weigh 1 pound in all. Each peach weighs the same amount. Peaches are on sale for $2.24 per pound. Write and solve an equation to find the cost p of one peach. Graph the solution on a number line.

Answer:
Given that,
Selena buys 4 peaches that weigh 1 pound in all.
Each peach weighs the same amount. Peaches are on sale for $2.24 per pound.
Since the total weight of peaches is 1 pound.
So the price of 4 peaches is $2.24.
Let p be the price of 1 peach.
4p = 2.24
p = 2.24/4
p = 0.56

Question 2.
STEM A 120-volt battery is connected to a circuit with 30 ohms of resistance. The current in amperes c flowing through the circuit can be found using the equation 30c = 120. How many amperes of current are in the wire?
Answer:
Given,
A 120-volt battery is connected to a circuit with 30 ohms of resistance.
The current in amperes c flowing through the circuit can be found using the equation 30c = 120.
30c = 120
c = 120/30
c = 4
There are 4 amperes of current in the wire.
Math on the Spot For Problems 3-4, solve each equation. Check your answer.
Question 3.
\(\frac{x}{7}\) = 2
Answer:
\(\frac{x}{7}\) = 2
x = 2 × 7
x = 14
Question 4.
36 = \(\frac{w}{4}\)
Answer:
36 = \(\frac{w}{4}\)
w/4 = 36
w = 36 × 4
w = 144
Question 5.
Mr. Falco baked blueberry muffins several times in May using the recipe shown. He used 3\(\frac{3}{4}\) cups of milk in all. How many times did he bake muffins? Use the equation \(\frac{1}{4}\)t = 3\(\frac{3}{4}\).

Answer:
Given,
Mr. Falco baked blueberry muffins several times in May using the recipe shown. He used 3\(\frac{3}{4}\) cups of milk in all.
\(\frac{1}{4}\)t = 3\(\frac{3}{4}\).
t = \(\frac{15}{4}\) × 4
t = 15
Question 6.
Model with Mathematics One ride on a city bus costs $1.50. Martina has $18 on her bus pass. Write and solve an equation to find how many rides she can take without loading more money on her bus pass. Explain.
Answer:
Given,
One ride on a city bus costs $1.50. Martina has $18 on her bus pass.
The equation would be
1.5x = 18
x = 18/1.5
x = 12
She can take 12 rides without loading more money on her bus pass.
For Problems 7-10, find each solution.
Question 7.
\(\frac{x}{3}\) = 16
x = ![]()
Answer:
\(\frac{x}{3}\) = 16
x = 16 × 3
x = 48
Question 8.
4x = 76
x = ![]()
Answer:
4x = 76
x = 76/4
x = 19
Question 9.
15x = 105
x = ![]()
Answer:
15x = 105
x = 105/15
x = 7
Question 10.
\(\frac{x}{8}\) = 10
x = ![]()
Answer:
\(\frac{x}{8}\) = 10
x = 10 × 8
x = 80
Test Prep
Question 11.
Bonnie buys 4 ounces of loose-leaf tea as a gift. The total cost of the tea is $25.00. Use the equation 4t = 25. How much does each ounce of tea cost?
Answer:
Given,
Bonnie buys 4 ounces of loose-leaf tea as a gift.
The total cost of the tea is $25.00.
By using the equation 4t = 25
4t = 25
t = 25/4
t = 6.25
Thus each ounce of tea cost $6.25.
Question 12.
Santos cuts a length of ribbon into 2-inch long pieces. He has enough ribbon to make 10 pieces. What is the total length of the ribbon that Santos has? Use the equation \(\frac{x}{2}\) = 10.
Answer:
Given,
Santos cuts a length of ribbon into 2-inch long pieces. He has enough ribbon to make 10 pieces.
\(\frac{x}{2}\) = 10.
x = 10 × 2
x = 20
Thus the total length of the ribbon that Santos has is 20 inches.
Question 13.
What is the solution to the equation 5x = 6?
(A) 1.2
(B) 0.83
(C) 1
(D) 30
Answer:
5x = 6
x = 6/5
x = 1.2
Option A is the correct answer.
Question 14.
Mr. Nakamoto’s gas tank is empty. He refills the 11.6-gallon tank in his car with gasoline that costs $2.58 per gallon. Which point on the number line shows how much Mr. Nakamoto pays for the gasoline? Use the equation \(\frac{x}{2.58}\) = 11.6.

(A) Point A
(B) Point B
(C) Point C
(D) Point D
Answer:
Given,
Mr. Nakamoto’s gas tank is empty. He refills the 11.6-gallon tank in his car with gasoline that costs $2.58 per gallon.
\(\frac{x}{2.58}\) = 11.6
x = 11.6 × 2.58
x = 29.9 ≈ 30
So it is located on point D.
Thus option D is the correct answer.
Spiral Review
Question 15.
What is the quotient of 13.5 ÷ 0.75?
Answer:
Change the divisor 0.75 to a whole number by moving the decimal point 2 places to the right. Then move the decimal point in the dividend the same, 2 places to the right.
We then have the equations:
1350 ÷ 75 = 18.000
and therefore:
13.5 ÷ 0.75 = 18.000
Both are calculated to 3 decimal places.
Thus the quotient of 13.5 ÷ 0.75 is 18
Question 16.
A grocery store sells long-grain rice for $2.49 per pound. Write an expression for the cost of y pounds of long grain rice.
Answer:
Given,
A grocery store sells long-grain rice for $2.49 per pound.
We need to write an expression for the cost of y pounds of long grain rice.
The expression is a product of the cost of y and price per pound 2.49y
Question 17.
Order the fractions from least to greatest.
\(\frac{3}{8}\), \(\frac{4}{12}\), \(\frac{4}{9}\), \(\frac{3}{6}\), \(\frac{1}{4}\)
Answer:
Given fractions,
\(\frac{3}{8}\), \(\frac{4}{12}\), \(\frac{4}{9}\), \(\frac{3}{6}\), \(\frac{1}{4}\)
The denominator with the greatest number will be the smallest fraction
Let us make all the denominators the same.
LCM is 72
\(\frac{3}{8}\) = \(\frac{27}{72}\)
\(\frac{4}{12}\) = \(\frac{24}{72}\)
\(\frac{4}{9}\) = \(\frac{32}{72}\)
\(\frac{3}{6}\) = \(\frac{36}{72}\)
\(\frac{1}{4}\) = \(\frac{18}{72}\)
\(\frac{27}{72}\), \(\frac{24}{72}\), \(\frac{32}{72}\), \(\frac{36}{72}\) and \(\frac{18}{72}\)
Now we can write the fractions from least to the greatest.
\(\frac{18}{72}\), \(\frac{24}{72}\), \(\frac{27}{72}\), \(\frac{32}{72}\) and \(\frac{36}{72}\) ×