Into Math Grade 6 Module 8 Lesson 1 Answer Key Understand and Apply Exponents

We included HMH Into Math Grade 6 Answer Key PDF Module 8 Lesson 1 Understand and Apply Exponents to make students experts in learning maths.

HMH Into Math Grade 6 Module 8 Lesson 1 Answer Key Understand and Apply Exponents

I Can write and evaluate numerical expressions involving whole-number exponents.

Spark Your Learning

Brianna needs to contact members of the softball league. She calls 4 members in the morning. Those 4 people each call 4 more people in the afternoon. That evening, those additional people each call 4 others. How many people are called that evening?

Answer:
The number of softball league members called by Brianna = 4
The 4 members who are called by Brianna were called to each 4 more people. That means 4 x 4 = 16 members.
These 16 members are called in the afternoon.
These 16 were called to another 4 members each in the evening.
finally, in the evening 16 x 4 = 64 are called.

Turn and Talk Is there another way to solve this problem? Explain.
Answer:

Build Understanding

Connect to Vocabulary
When a number is raised to a power, the number that is used as a factor is the base. An exponent is a number that indicates how many times the base is used as a factor.

Question 1.
A small company uses a phone tree to notify employees of cancellation due to bad weather. The manager calls 2 people. Then each of those people calls 2 more people, and so on.

A. Complete the table. What pattern(s) do you see?
Answer:
An exponent of a number represents the number of times the number is multiplied by itself. If 2 is multiplied by itself by n times, then, it is represented as:
2 x 2 x 2 x 2 x ……..n times = 2^n
The above expression, 2ⁿ, is said as 2 raised to the power n. Therefore, exponents are also called power or sometimes indices.
The general form of exponents:
The exponent is a simple but powerful tool. It tells us how many times a number should be multiplied by itself to get the desired result. Thus any number ‘a’ raised to power ‘n’ can be expressed as:

Here a is any number and n is a natural number.
aⁿ is also called the nth power of a.
‘a’ is the base and ‘n’ is the exponent or index or power.
‘a’ is multiplied ‘n’ times, and thereby exponentiation is the shorthand method of repeated multiplication.

The number of calls is in factor form.

B. Complete each statement to describe the pattern.

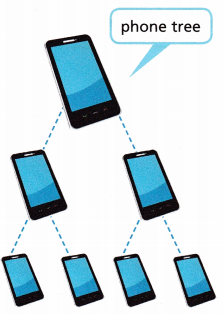
In the 2nd round of calls, the total number of calls in that round is equal to the product of two 2s.
In the 3rd round of calls, the total number of calls in that round is equal to the product of ____________ 2s.
In the 4th round of calls, the total number of calls in that round is equal to the product of ____________ 2s.
In the 5th round of calls, the total number of calls in that round is equal to the product of ____________ 2s.
Answer:
In the 3rd round of calls, the total number of calls in that round is equal to the product of four 2s
2 x 2 = 4 calls
In the 3rd round of calls, the total number of calls in that round is equal to the product of eight 2s
4 x 2 = 8 calls.
In the 3rd round of calls, the total number of calls in that round is equal to the product of sixteen 2s
8 x 2 = 16 calls.

C. How is the number of rounds of calling related to the number of times 2 is used as a factor?
Answer:
An exponent of a number represents the number of times the number is multiplied by itself. If 2 is multiplied by itself by n times, then, it is represented as:
2 x 2 x 2 x 2 x ……..n times = 2^n
The above expression, 2ⁿ, is said as 2 raised to the power n. Therefore, exponents are also called power or sometimes indices.
The general form of exponents:
The exponent is a simple but powerful tool. It tells us how many times a number should be multiplied by itself to get the desired result. Thus any number ‘a’ raised to power ‘n’ can be expressed as:

Now we can write as:
2 x 2 = 4
2 x 2 x 2 = 8
2 x 2 x 2 x 2 = 16
2 x 2 x 2 x 2 x 2 = 32

Turn and Talk When is it useful to write an expression using a base and an exponent? Give an example.
Answer:
In Mathematics, there are different laws of exponents. All the rules of exponents are used to solve many mathematical problems which involve repeated multiplication processes. The laws of exponents simplify the multiplication and division operations and help to solve the problems easily.
For example,
a^m = a × a × a × a…m times.
b⁴ = b × b × b × b.
5³ = 5 × 5 × 5.
The number a is known as base and m is said to be the exponent and a^m is said to be the exponent form of the number.
Exponents are also called powers or indices.
We read a^m as a raised to the power m or just a to the power m.
Rewrite 7 × 7 × 7 × 7 × 7 × 7, using an exponent.
solution:
Step 1: The number 7 appears six times in the multiplication.
Step 2: So 7 × 7 × 7 × 7 × 7 × 7 = 7⁶
Step 3: The expression 7⁶ has a base of 7 and an exponent of 6.

Step It Out

A dot is sometimes used instead of the symbol x to represent multiplication. You can use an exponent and a base to show the repeated multiplication of a factor. The expression shown is read as “7 to the 5th power.”

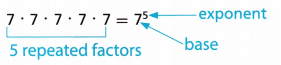
There are two specially named powers:
8² could be read as “8 to the 2nd power” or as “8 squared.”
9³ could be read as “9 to the 3rd power” or as “9 cubed.”

Question 2.
An exponent tells how many times a number is used in an expression. Look at the expression 5 • 5 • 5 • 5.
A. How many times is the factor 5 used?
Answer:
The number a is known as base and m is said to be the exponent and a^m is said to be the exponent form of the number.
Exponents are also called powers or indices.
We read a^m as a raised to the power m or just a to the power m.
Step 1: The number 5 appears four times in the multiplication.
Step 2: So 5 x 5 x 5 x 5 = 5^4
Step 3: The expression 5^4 has a base of 5 and an exponent of 4.

B. Complete each statement.
5 • 5 • 5 • 5 =
8 • 8 • 8 • 8 • 8 =
Answer:
The number 5 appears 4 times so 5 x 5 x 5 x 5 =
The number 8 appears 8 times so 8 x 8 x 8 x 8 x 8 =

C. Write an equivalent repeated multiplication expression.
2³ = × ×
(\(\frac{1}{3}\))⁵ = × × × ×
Answer:

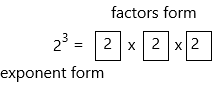
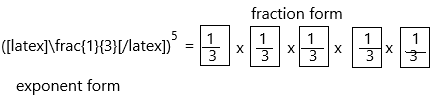
Question 3.
Find the value of each expression.
A. 5³ = × × =
Answer:
The number a is known as base and m is said to be the exponent and a^m is said to be the exponent form of the number.
Exponents are also called powers or indices.
We read a^m as a raised to the power m or just a to the power m.
Step 1: The number 5 appears four times in the multiplication.
Step 2: So 5 x 5 x 5 = 5^3
Step 3: The expression 5^3 has a base of 5 and an exponent of 3.
Step 4: The value of 5^3 is 125

B. 4⁵ = × × × × =
Answer:
The number a is known as base and m is said to be the exponent and a^m is said to be the exponent form of the number.
Exponents are also called powers or indices.
We read a^m as a raised to the power m or just a to the power m.
Step 1: The number 5 appears five times in the multiplication.
Step 2: So 4 x 4 x 4 x 4 x 4 = 4^5
Step 3: The expression 4^5 has a base of 4 and an exponent of 5.
Step 4: The value of 4^5 is 1024.

Check Understanding

Question 1.
A farming community begins with one resident. Then every year, the number of residents multiplies by 10. Write an expression using an exponent to represent the number of residents in the community after 5 years.
Answer: 10^5
Explanation:
The number of multiples increased by every year = 10
We need to write an expression using an exponent to represent the number of residents in the community after 5 years. Let it be X.
The exponent of a number tells us how many times the number is multiplied.
X = 10 ^ 5
X = 10 x 10 x 10 x 10 x 10
X = 100000.

Question 2.
On a tree, the trunk splits into 5 branches. Then each branch splits into 5 smaller branches, and each of those branches splits into 5 very thin branches. How many very thin branches are on the tree?
Answer:
The number of branches a trunk splits = 5
The number of small branches splitter by each branch = 5
The number of very thin branches = X

X = 5 x 5
X = 25
Therefore, the very thin branches are 25.

Question 3.
Explain the expression 2¹⁰. Complete the sentences.
A. The number is used as a repeated factor times.
Answer:
power is an expression that shows repeated multiplication of the same number or factor. The value of the exponent is based on the number of times the base is multiplied to itself.
.The number 2 is used as a repeated factor 10 times

B. The base of the expression is and the exponent is .
Answer:
The number a is known as base and m is said to be the exponent and a^m is said to be the exponent form of the number.
Exponents are also called powers or indices.
We read a^m as a raised to the power m or just a to the power m
The base of expression is 2 and the exponent is 10

C. The value of 2¹⁰ is .
Answer:
Step 1: The number 2 appears ten times in the multiplication.
Step 2: So 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 2¹⁰
Step 3: The expression 2¹⁰ has a base of 2 and an exponent of 10.
Step 4: The value of 2¹⁰ is 1024.

On Your Own

Question 4.
STEM A certain bacterium splits itself into 2 identical cells in 1 day. Each of those new cells is capable of splitting itself into 2 identical cells in 1 day. So the first day there are 2 cells, the second day there are 2 × 2 cells, and so on. Write and evaluate an expression using a base and an exponent to represent the number of cells present at the end of the 7th day.

Answer:
The number of cells a bacterium splits per day = 2
The number of cells it splits in two days = 2 x 2 = 4
The number of cells it splits at the end of 7th day = B
B = 2^7
B = 2 x 2 x 2 x 2 x 2 x 2 x 2
B = 128
therefore, on 7th day the bacterium splits into 128 identical cells.

Question 5.
Write each expression in exponential form.
A. 9 • 9 • 9 • 9 • 9 = _____________
Answer:
The number a is known as base and m is said to be the exponent and a^m is said to be the exponent form of the number.
Exponents are also called powers or indices.
We read a^m as a raised to the power m or just a to the power m.
Step 1: The number 9 appears five times in the multiplication.
Step 2: So 9 x 9 x 9 x 9 x 9 = 9^5
Step 3: The expression 9^5 has a base of 9 and an exponent of 5.
Step 4: The value of 9^5 is 59049

B. \(\frac{1}{8}\) • \(\frac{1}{8}\) • \(\frac{1}{8}\) = _____________
Answer:
The number a is known as base and m is said to be the exponent and a^m is said to be the exponent form of the number.
Exponents are also called powers or indices.
We read a^m as a raised to the power m or just a to the power m.
Step 1: The number 1/8 appears three times in the multiplication.
Step 2: So 1/8 x 1/8 x 1/8 = (1/8)^3
Step 3: The expression (1/8)^3 has a base of 1/8 and an exponent of 3.
Step 4: The value of (1/8)^3 is 1/512

For Problems 6-7, write the exponential expression as an equivalent repeated multiplication expression and then evaluate the expression.

Question 6.
6³ = ___________
Answer:
In Mathematics, there are different laws of exponents. All the rules of exponents are used to solve many mathematical problems which involve repeated multiplication processes. The laws of exponents simplify the multiplication and division operations and help to solve the problems easily.
For example,
a^m = a × a × a × a…m times.
b⁴ = b × b × b × b.
5³ = 5 × 5 × 5.
The number a is known as base and m is said to be the exponent and a^m is said to be the exponent form of the number.
Exponents are also called powers or indices.
We read a^m as a raised to the power m or just a to the power m.
Step 1: The number 6 appears three times in the multiplication.
Step 2: So 6 x 6 x 6 = 6^3
Step 3: The expression 6^3 has a base of 6 and an exponent of 3.
Step 4: The value of 6^3 is 216

Question 7.
2⁶ = _____________
Answer:
In Mathematics, there are different laws of exponents. All the rules of exponents are used to solve many mathematical problems which involve repeated multiplication processes. The laws of exponents simplify the multiplication and division operations and help to solve the problems easily.
For example,
a^m = a × a × a × a…m times.
b⁴ = b × b × b × b.
5³ = 5 × 5 × 5.
The number a is known as base and m is said to be the exponent and a^m is said to be the exponent form of the number.
Exponents are also called powers or indices.
We read a^m as a raised to the power m or just a to the power m.
Step 1: The number 2 appears six times in the multiplication.
Step 2: So 2 x 2 x 2 x 2 x 2 x 2 = 2^6
Step 3: The expression 2^6 has a base of 2 and an exponent of 6.
Step 4: The value of 2^6 is 64

Question 8.
Explain the expression 10⁵. Complete the sentences. The number is used as a repeated factor. is used as a factor times.
Answer:
The number 10 is used as a repeated factor. 5 is used as a factor time.
The number a is known as base and m is said to be the exponent and a^m is said to be the exponent form of the number.
Exponents are also called powers or indices.
We read a^m as a raised to the power m or just a to the power m.
Step 1: The number 2 appears six times in the multiplication.
Step 2: So 10 x 10 x 10 x 10 x 10 = 10⁵
Step 3: The expression 10⁵ has a base of 10 and an exponent of 5.
Step 4: The value of 10⁵ is 100000

Question 9.
Use Repeated Reasoning Carrie recruits 3 of her friends to sell candles to raise money for new playground equipment. The next day each of her 3 friends recruits 3 more friends. This pattern continues for 5 days. Write an exponential expression to represent the number of new recruits on the 5th day.
A. The number is used as a repeated factor times.
Answer:
The number a is known as base and m is said to be the exponent and a^m is said to be the exponent form of the number.
Exponents are also called powers or indices.
We read a^m as a raised to the power m or just a to the power m.
the number 9 is used as a repeated factor 5 times

B. Write the expression as an equivalent repeated multiplication expression. Then write it as an expression with an exponent.
× × × × =
Answer:
Step 1: The number 9 appears five times in the multiplication.
Step 2: So 9 x 9 x 9 x 9 x 9 = 9^5
Step 3: The expression 9^5 has a base of 9 and an exponent of 5.
Step 4: The value of 9^5 is 59049

I’m in a Learning Mindset!

What facts about exponents can I talk about?
Answer:
Zero raised to any power is zero (e.g. 0⁵ = 0)
One raised to any power is one (e.g. 1⁵ = 1)
Any number raised to the zero power is one (e.g. 7⁰ = 1)
Any number raised to the first power is that number (e.g. 7¹ = 7)

Lesson 8.1 More Practice/Homework

Question 1.
Explain the expression 128. Complete the sentences.
The number is used as a repeated factor. is used as a factor times.
Answer:
the number 2 is used as a repeated factor. 2 is used as a factor 7 times.
The number a is known as base and m is said to be the exponent and a^m is said to be the exponent form of the number.
Exponents are also called powers or indices.
We read a^m as a raised to the power m or just a to the power m.
Step 1: The number 2 appears seven times in the multiplication.
Step 2: So 2 x 2 x 2 x 2 x 2 x 2 x 2 = 2^7
Step 3: The expression 2^7 has a base of 2 and an exponent of 7.
Step 4: The value of 2^7 is 128

Question 2.
Use Repeated Reasoning At 4 o’clock, Devon called 6 friends to let them know that the weather forecast called for snow. At 6 o’clock, each of his friends called 6 other friends. At 8 o’clock, each of those friends called 6 of their other friends.

A. Write an expression to represent the number of people called at 6 o’clock using a base and an exponent.
Answer:
The number a is known as base and m is said to be the exponent and a^m is said to be the exponent form of the number.
Exponents are also called powers or indices.
We read a^m as a raised to the power m or just a to the power m.
Step 1: The number 6 appears six times in the multiplication.
Step 2: So 6 x 6 x 6 x 6 x 6 x 6 = 6^6
Step 3: The expression 6^6 has a base of 6 and an exponent of 6.
Step 4: The value of 6^6 is 46656

B. Write an expression to represent the number of people called at 8 o’clock using a base and an exponent.
Answer:
The number a is known as base and m is said to be the exponent and a^m is said to be the exponent form of the number.
Exponents are also called powers or indices.
We read a^m as a raised to the power m or just a to the power m.
Step 1: The number 6 appears six times in the multiplication.
Step 2: So 6 x 6 x 6 x 6 x 6 x 6 x 6 x 6  = 6^8
Step 3: The expression 6^8 has a base of 6 and an exponent of 8.
Step 4: The value of 6^8 is 1679616

C. How many people were called in all? Explain.
Answer:
As I mentioned above.
At 8 o’clock, each of those friends called 6 of their other friends. This was the end.
Step 1: The number 6 appears six times in the multiplication.
Step 2: So 6 x 6 x 6 x 6 x 6 x 6 x 6 x 6  = 6^8
Step 3: The expression 6^8 has a base of 6 and an exponent of 8.
Step 4: The value of 6^8 is 1679616
Therefore, 1679616 were called.

Question 3.
Reason Compare the expressions 3⁸ and 3⁵ × 3³ using the properties of multiplication. What do you notice?
Answer:
As per the multiplication law of exponents, the product of two exponents with the same base and different powers equals to base raised to the sum of the two powers or integers.
a^m × aⁿ  = a^m+n
The above-given 3⁵ × 3³
According to the multiplication law of exponents:
3^5 x 3^3
= 3^(5 +3)
= 3^8

Question 4.
Math on the Spot Write the expression in exponential form.
A. 7 • 7 • 7 • 7 = ___________
Answer:
The number a is known as base and m is said to be the exponent and a^m is said to be the exponent form of the number.
Exponents are also called powers or indices.
We read a^m as a raised to the power m or just a to the power m.
Step 1: The number 7 appears four times in the multiplication.
Step 2: So 7 x 7 x 7 x 7 = 7^4
Step 3: The expression 7^4 has a base of 7 and an exponent of 4.
Step 4: The value of 7^4 is 2401

B. 3 • 3 • 3 • 3 • 3 • 3 = ____________
Answer:
The number a is known as base and m is said to be the exponent and a^m is said to be the exponent form of the number.
Exponents are also called powers or indices.
We read a^m as a raised to the power m or just a to the power m.
Step 1: The number 3 appears six times in the multiplication.
Step 2: So 3 x 3 x 3 x 3 x 3 x 3 = 3^6
Step 3: The expression 3^6 has a base of 3 and an exponent of 6.
Step 4: The value of 3^6 is 729

For Problems 5-6, write the exponential expression as an equivalent repeated multiplication expression and then evaluate the expression.

Question 5.
2⁸ = ___________
Answer:
In Mathematics, there are different laws of exponents. All the rules of exponents are used to solve many mathematical problems which involve repeated multiplication processes. The laws of exponents simplify the multiplication and division operations and help to solve the problems easily.
For example,
a^m = a × a × a × a…m times.
b⁴ = b × b × b × b.
5³ = 5 × 5 × 5.
The number a is known as base and m is said to be the exponent and a^m is said to be the exponent form of the number.
Exponents are also called powers or indices.
We read a^m as a raised to the power m or just a to the power m.
Step 1: The number 2 appears eight times in the multiplication.
Step 2: So 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 2^8
Step 3: The expression 2^8 has a base of 2 and an exponent of 8.
Step 4: The value of 2^8 is 256

Question 6.
5⁵ = ___________________
Answer:
In Mathematics, there are different laws of exponents. All the rules of exponents are used to solve many mathematical problems which involve repeated multiplication processes. The laws of exponents simplify the multiplication and division operations and help to solve the problems easily.
For example,
a^m = a × a × a × a…m times.
b⁴ = b × b × b × b.
5³ = 5 × 5 × 5.
The number a is known as base and m is said to be the exponent and a^m is said to be the exponent form of the number.
Exponents are also called powers or indices.
We read a^m as a raised to the power m or just a to the power m.
Step 1: The number 5 appears five times in the multiplication.
Step 2: So 5 x 5 x 5 x 5 x 5 = 5^5
Step 3: The expression 5^5 has a base of 5 and an exponent of 5.
Step 4: The value of 5^5 is 3125

For Problems 7 and 8, write the repeated multiplication expression using a single exponent.

Question 7.
8 • 8 • 8 • 8 • 8 = __________
Answer:
In Mathematics, there are different laws of exponents. All the rules of exponents are used to solve many mathematical problems which involve repeated multiplication processes. The laws of exponents simplify the multiplication and division operations and help to solve the problems easily.
For example,
a^m = a × a × a × a…m times.
b⁴ = b × b × b × b.
5³ = 5 × 5 × 5.
The number a is known as base and m is said to be the exponent and a^m is said to be the exponent form of the number.
Exponents are also called powers or indices.
We read a^m as a raised to the power m or just a to the power m.
Step 1: The number 8 appears five times in the multiplication.
Step 2: So 8 x 8 x 8 x 8 x 8 = 8^5
Step 3: The expression 8^5 has a base of 8 and an exponent of 5.
Step 4: The value of 8^5 is 32768

Question 8.
4 • 4 • 4 • 4 • 4 • 4 • 4 = ____________
Answer:
In Mathematics, there are different laws of exponents. All the rules of exponents are used to solve many mathematical problems which involve repeated multiplication processes. The laws of exponents simplify the multiplication and division operations and help to solve the problems easily.
For example,
a^m = a × a × a × a…m times.
b⁴ = b × b × b × b.
5³ = 5 × 5 × 5.
The number a is known as base and m is said to be the exponent and a^m is said to be the exponent form of the number.
Exponents are also called powers or indices.
We read a^m as a raised to the power m or just a to the power m.
Step 1: The number 4 appears seven times in the multiplication.
Step 2: So 4 x 4 x 4 x 4 x 4 x 4 x 4 = 4^7
Step 3: The expression 4^7 has a base of 4 and an exponent of 7.
Step 4: The value of 4^7 is 16384

Test Prep

Question 9.
Select all expressions equivalent to 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3.
(A) 8³
(B) 3⁸
(C) 3⁵ • 3³
(D) 3⁴ • 3⁴
(E) 3⁷ • 3²
Answer: Option B, C, D are the possible expressions.
Option B:
3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 = 3^8
3 is used as a repeated factor of 8 times.
Option C:
As per the multiplication law of exponents, the product of two exponents with the same base and different powers equals to base raised to the sum of the two powers or integers.
a^m × aⁿ  = a^m+n
The above-given 3⁵ × 3³
According to the multiplication law of exponents:
3^5 x 3^3
= 3^(5 +3)
= 3^8
Option D:
According to the multiplication law of exponents:
3^4 x 3^4
= 3^(4 +4)
= 3^8

Question 10.
Select all expressions equivalent to 11 • 11 • 11.
(A) 11³
(B) 3¹¹
(C) 11¹ • 11³
(D) 3⁵ • 3⁶
(E) 11¹ • 11²
Answer: Option A and E are the possible expressions.
Option A:
11. 11. 11 = 11^3
3 is used as a repeated factor of 8 times.
Option E:
As per the multiplication law of exponents, the product of two exponents with the same base and different powers equals to base raised to the sum of the two powers or integers.
a^m × aⁿ  = a^m+n
The above-given 11^1. 11^2
According to the multiplication law of exponents:
= 11^(1 +2)
= 11^3

Question 11.
Write two equivalent expressions, one exponential and one a product of factors, for “4 to the 5th power.” Evaluate the expressions.
Answer:
4 to the 5th power can be written as 4^5
4^5 can be written as: 4 x 4 x 4 x 4 x 4
In Mathematics, there are different laws of exponents. All the rules of exponents are used to solve many mathematical problems which involve repeated multiplication processes. The laws of exponents simplify the multiplication and division operations and help to solve the problems easily.
For example,
a^m = a × a × a × a…m times.
b⁴ = b × b × b × b.
5³ = 5 × 5 × 5.
The number a is known as base and m is said to be the exponent and a^m is said to be the exponent form of the number.
Exponents are also called powers or indices.
We read a^m as a raised to the power m or just a to the power m.
Step 1: The number 4 appears five times in the multiplication.
Step 2: So 4 x 4 x 4 x 4 x 4 = 4^5
Step 3: The expression 4^5 has a base of 4 and an exponent of 5.
Step 4: The value of 4^5 is 1024
2nd method:
We can go for the multiplication law of exponents:
As per the multiplication law of exponents, the product of two exponents with the same base and different powers equals to base raised to the sum of the two powers or integers.
a^m × aⁿ  = a^m+n
According to the multiplication law of exponents:
4^1 x 4^4
= 4^(1 +4)
= 4^5

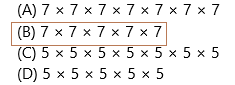
Question 12.
Select the correct expanded form of 7⁵.
(A) 7 × 7 × 7 × 7 × 7 × 7 × 7
(B) 7 × 7 × 7 × 7 × 7
(C) 5 × 5 × 5 × 5 × 5 × 5 × 5
(D) 5 × 5 × 5 × 5 × 5
Answer: Option B is correct

In Mathematics, there are different laws of exponents. All the rules of exponents are used to solve many mathematical problems which involve repeated multiplication processes. The laws of exponents simplify the multiplication and division operations and help to solve the problems easily.
For example,
a^m = a × a × a × a…m times.
b⁴ = b × b × b × b.
5³ = 5 × 5 × 5.
The number a is known as base and m is said to be the exponent and a^m is said to be the exponent form of the number.
Exponents are also called powers or indices.
We read a^m as a raised to the power m or just a to the power m.
Step 1: The number 7 appears five times in the multiplication.
Step 2: So 7 x 7 x 7 x 7 x 7 = 7^5
Step 3: The expression 7^5 has a base of 7 and an exponent of 5.

Spiral Review

Question 13.
Letty answered 15 out of 20 questions correctly on her history quiz. What is her grade as a percent?
Answer:
The number of questions Letty answered = 15
The total number of questions = 20
The grade as a percent = P
P = 15/20 x 100
P = 75%
therefore, Letty grade is 75%.

Question 14.
1 kilogram is equivalent to about 2.2 pounds. An orangutan weighs 142 pounds. What is its mass in kilograms?
Answer:
1 kg = 2.2 pounds
The weight of an orangutan = 142
The mass in kilograms = K

therefore, the weight is kgs is 64.54

Question 15.
Which is the better buy, a 31-ounce bottle of ketchup for $2.53 or a 64-ounce bottle for $5.05?
Answer:
I think a 64-ounce bottle is better to buy.
The cost of 31-ounce bottle = $2.53
The cost of 64-ounce bottle = $5.05
If we buy 2 31-ounce bottles then we need to spend $5.06 which e get 62-ounces.
But if we buy a 64-ounce bottle, we get 2-ounces more with 0.1 less. So definitely better worth buying a 64-ounce bottle.

Question 16.
A pancake recipe calls for 4\(\frac{1}{2}\) cups of whole-wheat flour. If the chef wants to split the recipe into 3 equal batches, how much flour should be in each batch?
Answer:
4 1/2 can be written as 9/2 which is an improper fraction
Now, this 9/2 should be divided into 3 equal batches. Then we get to know the flour should be in each batch. Let it be E.
E = 9/2 x 3
E = 27/2
E = 13.5
Therefore, each batch would get 13.5 cups of flour.