We included HMH Into Math Grade 6 Answer Key PDF Module 6 Lesson 2 Use Rate Reasoning to Convert Within Measurement Systems to make students experts in learning maths.
HMH Into Math Grade 6 Module 6 Lesson 2 Answer Key Use Rate Reasoning to Convert Within Measurement Systems
I Can write and use equivalent fractions or conversion factors to convert units within a measurement system.

Spark Your Learning
Milo is making 1\(\frac{1}{2}\) batches of muffins for a bake sale. If each batch of muffins calls for 1\(\frac{3}{4}\) cups of flour, how much flour will he need?

Turn and Talk How is multiplying fractions similar to multiplying whole numbers or decimals? How is it different? Explain.
Given,
Milo is making 1\(\frac{1}{2}\) batches of muffins for a bake sale.
Each batch of muffins calls for 1\(\frac{3}{4}\) cups of flour.
1\(\frac{1}{2}\) × 1\(\frac{3}{4}\)
Convert from mixed fractions to the improper fractions
1\(\frac{1}{2}\) can be written as \(\frac{3}{2}\)
1\(\frac{3}{4}\) can be written as \(\frac{7}{4}\)
\(\frac{3}{2}\) × \(\frac{7}{4}\) = \(\frac{3×7}{2×4}\) = \(\frac{21}{8}\)
Now convert from improper fraction to the mixed fraction.
\(\frac{21}{8}\) = 2 \(\frac{5}{8}\)
Build Understanding
You can use equivalent rates to convert both customary and metric units. Use the table to convert one unit to another unit within the same measurement system.
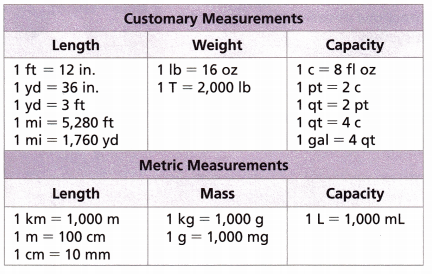
1. Heather needs to mail the package shown. The weight on the display is in pounds. The shipping company charges by the ounce. How many ounces does the package weigh?

A. How many ounces are in one pound?
______________________
Answer: There are 16 ounces in one pound.
1 pound = 16 oz.
B. What rate could you use to convert 4 pounds into ounces?
______________________
Answer:
1 pound = 16 oz.
4 pounds = x
x × 1 = 4 × 16 oz.
x = 64 oz.
There are 64 ounces in 4 pounds.
C. Use equivalent rates to convert 4 pounds into ounces.
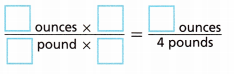
Answer:
D. How many ounces are in 4 pounds?
![]() pounds is equal to
pounds is equal to ![]() ounces.
ounces.
Answer: 4 pounds is equal to 64 ounces.
Turn and Talk How can you convert units within a measurement system?
Answer: We can convert within the metric system by multiplying or dividing the number by the value of the prefix. To convert from one unit to another within the metric system usually means moving a decimal point.
Step It Out
Another way to convert measurements is by using a conversion factor.
2. In Paris, the sculpture Long-Term Parking, created by Armand Fernandez, contains 60 cars embedded in 40,000 pounds of concrete. How many tons of concrete are in 40,000 pounds?
Connect to Vocabulary
A conversion factor is a rate in which two quantities are equal, but use different units.
A. Find the conversion factor comparing tons to pounds.


Answer:
1 ton = 2000 pounds
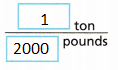
B. Multiply the conversion factor by 40,000 pounds.

Answer:
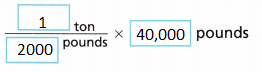
C. Simplify the expression.

Answer:

D. How many tons of concrete are in 40,000 pounds?
______________________
Answer:
1 ton = 2000 pounds
x = 40,000 pounds
x × 2000 = 40000
x = 40000/2000
x = 20
Thus 20 tons of concrete are in 40,000 pounds
Turn and Talk Explain how you know how to set up the conversion factor.
3. A bag of flour has a mass of 4.5 kilograms. How many grams are in 4.5 kilograms?
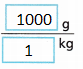
A. Write a conversion factor comparing kilograms to grams.
Answer:
1 kilogram = 1000 grams
B. Multiply the conversion factor by 4.5 kilograms.
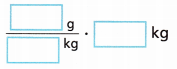
Answer:

C. Simplify the expression.
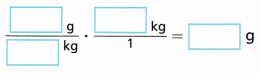
Answer:

D. How many grams are in 4.5 kilograms? _______
Answer:
1 kilogram = 1000 grams
4.5 kilograms = 4.5 × 1000 = 4500 grams
So, 4.5 kg = 4500 grams
4. A camel can drink 25 gallons of water in 10 minutes. How many cups of water can the camel drink in 10 minutes?
A. I need to find the conversion factor for gallons to cups, but the conversion table does not show this conversion. The table does show that
![]() cups =
cups = ![]() quart, and that
quart, and that ![]() quarts =
quarts = ![]() gallon.
gallon.
Complete the table of equivalent ratios to compare cups to quarts.

Answer:

4 cups = 1 quart
4 quarts = 1 gallon
B. How many cups are in 1 gallon?
![]() quarts =
quarts = ![]() gallon, so 1 gallon =
gallon, so 1 gallon = ![]() cups
cups
Answer:
1 quart = 0.25 gallon
1 gallon = 16 cups
Thus there are 16 cups in 1 gallon.
C. Multiply the conversion factor by 25 gallons.

Answer:
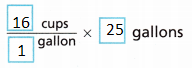
D. How many cups are in 25 gallons?
_____________
Answer:
Convert from gallons to cups.
1 gallon = 16 cups
25 gallons = x
x × 1 = 16 × 25
x = 400 cups
There are 400 cups in 25 gallons.
Check Understanding
Question 1.
The 1,600-meter race in the Olympics is very close to 1 mile long. How many kilometers is 1,600 meters? Show your work using equivalent ratios.

Answer:
Given,
The 1,600-meter race in the Olympics is very close to 1 mile long.
We have to find how many kilometers is 1,600 meters.
Convert from meters to kilometers
1000 meters = 1 kilometer
1600 meters = x
x × 1000 = 1600 × 1
x = 1600/1000
x = 1.6
1600 meters = 1.6 km
Question 2.
Scott is 72 inches tall. How many feet tall is Scott? Use a conversion factor to show your work.
Answer:
Given,
Scott is 72 inches tall.
12 inches = 1 feet
72 inches = x
x × 12 = 1 × 72
x = 72/12
x = 6
Therefore Scott is 6 feet tall.
Question 3.
Jill has 15 feet of ribbon. How many yards of ribbon does she have? Use a conversion factor to show your work.
Answer:
Given,
Jill has 15 feet of ribbon.
We have to convert from feet to yards.
1 feet = 0.3 yard
15 feet = 15 × 0.3 = 5 yards
Thus she has 5 yards of ribbon.
On Your Own
Question 4.
Karen is preparing 4.5 liters of punch. How many milliliters are in 4.5 liters?
Answer:
Given,
Karen is preparing 4.5 liters of punch.
We have to convert from liters to milliliters.
1 liter = 1000 milliliters
4.5 liter = x
x × 1 = 1000 × 4.5
x = 4500 milliliters
Thus there are 4500 milliliters in 4.5 liters.
Question 5.
Chen’s pedometer says he has walked 5,600 meters today. How many kilometers has Chen walked today?

Answer:
Given,
Chen’s pedometer says he has walked 5,600 meters today.
Convert from meters to kilometers.
1000 meters = 1 kilometer
5600 meters = x
x × 1000 = 5600 × 1
1000x = 5600
x = 5600/1000
x = 5.6
Thus Chen walked 5.6 kilometers today.
Question 6.
Critique Reasoning Doug says that 3,000 kilometers is the same distance as 3 meters. What mistake did he make converting 3 meters to kilometers?
Answer:
Given,
Doug says that 3,000 kilometers is the same distance as 3 meters.
1 kilometer = 1000 meters
x = 3 meters
x × 1000 = 3 × 1
x = 3/1000
x = 0.003
3 meters is equal to 0.003 kilometers
Question 7.
Reason A truck weighs 9,000 pounds. A repair shop sends a tow truck that can pull up to 5 tons. Can the tow truck tow the truck? Explain.
Answer:
Given,
A truck weighs 9,000 pounds. A repair shop sends a tow truck that can pull up to 5 tons.
Convert from Tons to pounds
1 ton = 2000 pounds
5 tons = x
x = 2000 × 5
x = 10,000 pounds
Thus 5 tons = 10,000 pounds
A truck weighs 9,000 pounds.
The truck cannot tow the truck.
Question 8.
Morgan has 42 inches of rope, Malcolm has 4 feet of rope, and Roberto has 2 yards of rope. Express the total length of rope the three friends have in inches, feet, and yards.
![]() inches =
inches = ![]() feet =
feet = ![]() yards
yards
Answer:
Given,
Morgan has 42 inches of rope, Malcolm has 4 feet of rope, and Roberto has 2 yards of rope.
Convert from inches to feet and feet to yards
1 feet = 12 inch
42 inches = 3.5 feet
Now convert from feet to yards
1 feet = 0.3 yards
3.5 feet = 1.16 yards
42 inches = 3.5 feet = 1.16 yards
Question 9.
What conversion factor can you use to convert miles to inches? Explain how you found it.
______________________
______________________
Answer:
The length in inches is equal to the miles multiplied by 63,360.
You can use online conversion to convert from miles to inches.
For Problems 10-15, convert the units.
Question 10.
8ft = ![]() in.
in.
Answer:
Convert from feet to inches.
1 feet = 12 inches
8 feet = x
x × 1 = 12 × 8
x = 96
So, 8 feet = 96 inches
Question 11.
12 yd = ![]() ft
ft
Answer:
Convert from yards to feet
1 yard = 3 feet
12 yards = x
x × 1 = 3 × 12
x = 36
So, 12 yards = 36 feet
Question 12.
![]() km = 11,250 m
km = 11,250 m
Answer:
Convert from meters to kilometers.
1000 meters = 1 km
11250 meters = x
x × 1000 = 1 × 11250
x = 11250/1000
x = 11.25
So, 11.25 km = 11,250 meters
Question 13.
![]() mg = 3.5 g
mg = 3.5 g
Answer:
Convert from grams to milligrams
1 gram = 1000 milligrams
3.5 gram = x
x × 1 = 1000 × 3.5
x = 3500
3500 mg = 3.5g
Question 14.
150 mL = ![]() L
L
Answer:
Convert from milliliters to liters
1000 ml = 1 liter
150 ml = x
x × 1000 = 150 × 1
x = 150/1000
x = 0.15 liter
150 mL = 0.15 L
Question 15.
![]() in. = 0.5 ft
in. = 0.5 ft
Answer:
Convert from feet to inch
1 feet = 12 inch
0.5 feet = x
x × 1 = 12 × 0.5
x = 6
So, 6 in = 0.5 ft
Question 16.
Open Ended Give an example of an item often measured with customary units and an item often measured with metric units.
Answer:
Baking a cake that requires one teaspoon (customary unit) of baking soda, which could also be converted into four grams (SI unit).
Question 17.
Aisling runs 5.5 kilometers and Fiona runs 6,250 meters. Who runs farther? Explain how you know.
Answer:
Given,
Aisling runs 5.5 kilometers and Fiona runs 6,250 meters.
Convert from kilometers to meters.
1 kilometer = 1000 meters
5.5 kilometers = x
x × 1 = 1000 × 5.5
x = 5500 meters
5500 < 6250
Thus Fiiona runs farther than Aisling.
Question 18.
Critique Reasoning Vince and Larry are converting 1 kilogram to milligrams. Larry reports that there are 2,000 milligrams in 1 kilogram, and Vince reports that there are 1,000,000 milligrams in 1 kilogram. Who is correct and why? Explain.
Answer: Vince is correct
Explanation:
Vince and Larry are converting 1 kilogram to milligrams.
Larry reports that there are 2,000 milligrams in 1 kilogram, and Vince reports that there are 1,000,000 milligrams in 1 kilogram.
Convert from kilograms to milligrams
1 kilogram = 1000000 milligrams
1 kilogram = 1000 grams
Question 19.
Howard is 176 centimeters tall. How tall is Howard in meters? _____________
Answer:
Given,
Howard is 176 centimeters tall.
Convert from centimeter to meter
100 centimeter = 1 meter
176 centimeter = x
x × 100 = 1 × 176
x = 176/100
x = 1.76 meter
Howard is 1.76 meter long.
Question 20.
A football field, not including the end zones, is 100 yards long. How long is the football field in feet?
______________________
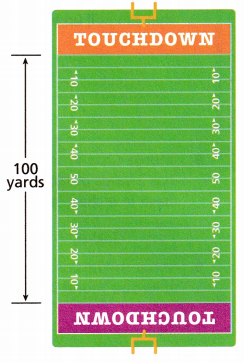
Answer:
Given,
A football field, not including the end zones, is 100 yards long.
Convert from yards to feet.
1 yard = 3 feet
100 yards = x
x × 1 = 3 × 100
x = 300 feet
The football field is 300 feet long.
Question 21.
A pitcher can hold 5 quarts of water. How many pints of water can the pitcher hold?
______________________
Answer:
Given,
A pitcher can hold 5 quarts of water.
Convert from quarts to pints.
1 quart = 2 pints
5 quarts = x
x = 2 × 5 = 10
5 quarts = 10 pints
The pitcher can hold 10 pints of water.
For Problems 22-25, compare the measurements using <, =, or >.
Question 22.
75 in. ![]() 7 ft
7 ft
Answer: <
Convert from feet to inches.
1 feet = 12 inches
7 feet = 12 × 7 = 84 inches
75 in. < 84 in.
Therefore 75 in. < 7 ft
Question 23.
8,465 lb ![]() 4 T
4 T
Answer: 8,465 lb > 4 T
Convert from pounds to tons.
1 ton = 2000 lbs
4 tons = 4 × 2000 = 8000 lbs
8465 lb > 8000 lbs
So, 8,465 lb > 4 T
Question 24.
2.7 m ![]() 270 cm
270 cm
Answer: 2.7 m = 270 cm
Convert from meters to centimeters
1 m = 100 cm
2.7 m = 2.7 × 100 = 270 cm
2.7 m = 270 cm
Question 25.
10 mi ![]() 10,000 ft
10,000 ft
Answer: 10 mi > 10,000 ft
Convert from miles to feet
1 mile = 5280 ft
10 miles = 10 × 5280 = 52800 ft
So, 10 mi > 10,000 ft
I’m in a Learning Mindset!
Did I have confidence in my answer for Task 1? What specific evidence do I have that I solved it correctly?
Lesson 6.2 More practice/Homework
Use Rate Reasoning to Convert Within Measurement Systems
Question 1.
Angela has 3 gallons of milk. How many quarts of milk does she have?
_________________________
Answer:
Given,
Angela has 3 gallons of milk.
Convert from gallons to quarts.
1 gallon = 4 quarts
3 gallons = 3 × 4 = 12 quarts
Thus she has 12 quarts of milk.
Math on the Spot For Problems 2-3, use conversion factors.
Question 2.
Convert 40 yards to feet.
_________________________
Answer:
Convert from yards to feet
1 yard = 3 feet
40 yards = 3 × 40 = 120 feet
Question 3.
Convert 20 quarts to gallons.
_________________________
Answer:
Convert from quarts to gallons
1 quart = 0.25 gallon
20 quart = 0.25 × 20 = 5 gallons
So, 20 quarts = 5 gallons
Question 4.
A sink can hold 10 gallons of water. How many quarts of water can the sink hold?
_________________________

Answer:
Given,
A sink can hold 10 gallons of water.
Convert from gallons to quarts.
1 gallon = 4 quarts
10 gallons = x
x × 1 = 4 × 10
x = 40
Thus 10 gallons = 40 quarts
Therefore the sink can hold 40 quarts of water.
Question 5.
A box weighs 64 ounces. What is the weight of the box in pounds?
______________________
Answer:
Given,
A box weighs 64 ounces.
Convert from ounces to pounds
16 ounces = 1 pound
64 ounces = x
x × 16 = 1 × 64
x = 64/16
x = 4
Thus the weight of the box in pounds is 4.
Question 6.
Reason Greg already has 2 gallons of paint to paint his living room. He estimates that he will need 10 quarts of paint. Does he have enough paint? Show your work.
______________________
Answer:
Given,
Greg already has 2 gallons of paint to paint his living room.
He estimates that he will need 10 quarts of paint.
Convert from gallons to quarts
1 gallon = 4 quarts
2 gallons = 2 × 4 = 8 quarts
8 is less than 10.
Thus Greg does not have enough paint.
Question 7.
Two bottles of water have a mass of 4 kilograms. How many grams is 4 kilograms?
______________________
Answer:
Given,
Two bottles of water have a mass of 4 kilograms.
Convert from kilograms to grams.
1 kilogram = 1000 grams
4 kilograms = x
x = 1000 × 4 = 4000 grams
4000 grams is 4 kilograms.
For Problems 8-13, convert to the unit indicated in parentheses. Then compare the measurements using <, =, or >.
Question 8.
5,000 m ![]() 4.9 km; (meters)
4.9 km; (meters)
Answer: 5000 m > 4.9 km
Convert from kilometers to meters
1 km = 1000 meters
4.9 km = 1000 × 4.9 = 4900 meters
5000 m > 4900m
5000 m > 4.9 km
Question 9.
4 lb ![]() 60 oz; (ounces)
60 oz; (ounces)
Answer: 4 lb > 60 oz
Convert from pounds to ounces
16 ounces = 1 pound
x = 4 pounds
x = 16 × 4
x = 64 oz
So, 4 lb > 60 oz.
Question 10.
3 mi ![]() 15,840 ft; (feet)
15,840 ft; (feet)
Answer: 3 mi. = 15,840 ft
Convert from miles to feet
1 mile = 5280 ft
3 miles = x
x = 3 × 5280
x = 15,840 feet
3 mile = 15,840 ft
Question 11.
72 in. ![]() 2 yd; (feet)
2 yd; (feet)
Answer: 72 in. = 2 yd
Convert from inches to yards
1 yard = 36 in.
2 yard = x
x = 2 × 36 = 72 in
So, 72 in. = 2 yards
Question 12.
0.45 L ![]() 4,200 mL; (milliliters)
4,200 mL; (milliliters)
Answer: 0.45 L < 4200 mL
Convert from liters to milliliters
1 liter = 1000 mL
0.45 liter = 0.45 × 1000 = 450 milliliters
So, 0.45L < 4200 mL
Question 13.
1.2 g ![]() 950 mg; (milligrams)
950 mg; (milligrams)
Answer: 1.2 g > 950 mg
Convert from grams to milligrams.
1 gram = 1000 milligrams
1.2 gram = x
x × 1 = 1000 × 1.2
x = 1200 milligrams
1200 mg > 950 mg
1.2 g > 950 mg
Test Prep
Question 14.
Write the following measurements in order from least to greatest: 0.04 kilometers, 420 centimeters, 4,600 millimeters, 4.3 meters
____________________
____________________
Answer: 420 centimeters, 4.3 meters, 4600 millimeters, 0.04 kilometers
Question 15.
Which of the following measurements is equivalent to 528 feet? Select all that apply.
A. 176 yards
B. 5,280 inches
C. 44 inches
D. 0.1 mile
E. 6,336 inches
Answer:
Convert from feet to inches
1 feet = 12 inches
528 feet = 12 × 528 = 6336 inches
Option E is the correct answer.
Convert from feet to yards
1 feet = 0.3 yard
528 feet = 176 yards
Option A is the correct answer.
Convert from feet to the mile
1 feet = 0.0001 mile
528 feet = 0.1 mile
Option D is the correct answer.
Thus Option A, D, and E is the correct answer.
Question 16.
One quart of milk costs $1.05 and 1 gallon of milk costs $3.89. Which is a better buy? Explain.
Answer:
Given,
One quart of milk costs $1.05 and
1 gallon of milk costs $3.89.
Convert from gallon to quarts
1 gallon = 4 quarts
3.89/4 = $0.97
It is better to buy 1 gallon of milk for $3.89
Question 17.
Which of the following measurements is equivalent to 400 grams?
A. 4 kilograms
B. 0.4 kilogram
C. 0.04 kilogram
D. 0.004 kilogram
Answer:
Convert from grams to kilograms.
1 gram = 0.001 kg
400 grams = x
x = 400 × 0.001 = 0.4 kg
Thus Option B is the correct answer.
Question 18.
Mairead jogs 2,700 feet, while Paula jogs 0.5 mile. Who jogs farther, and by how many feet?
Answer:
Given,
Mairead jogs 2,700 feet, while Paula jogs 0.5 mile.
Convert from mile to feet
1 mile = 5280 ft
0.5 mile = 2640 ft
2700 > 2640
2700 – 2640 = 60
Thus Mairead jogs farther than Paula with difference of 60 feet.
Spiral Review
Question 19.
Kelly is trying to decide which plan to use to download songs. She can download 8 songs for $9.60 or 15 songs for $15.00. Which plan offers the lowest cost per song? Explain.
Answer:
Given,
Kelly is trying to decide which plan to use to download songs.
She can download 8 songs for $9.60 or 15 songs for $15.00.
15 ÷ 15 = 1
9.60 ÷ 8 = 1.2
The plan to download 15 songs for $15 is better.
Question 20.
There are 10 seniors and 15 juniors in a gym class. What is the ratio of seniors to total students?
Answer:
Given,
There are 10 seniors and 15 juniors in a gym class.
Ratio is 10:15 = 2:3
Thus the ratio of seniors to total students is 2:3
Question 21.
Polly buys 6.8 yards of fabric for $28.90. What is the cost per yard?
Answer:
Given,
Polly buys 6.8 yards of fabric for $28.90.
28.90 ÷ 6.8 = $4.25
Thus the cost per yard is $4.25
Question 22.
What is the distance between -7 and its opposite on a number line?
Answer:
The opposite of -7 is 7.
-7 + 7 = 0
The difference between -7 and 7 is 0.