We included HMH Into Math Grade 6 Answer Key PDF Module 3 Lesson 5 Practice Fraction Operations to make students experts in learning maths.
HMH Into Math Grade 6 Module 3 Lesson 5 Answer Key Practice Fraction Operations
I Can use the LCM and GCF to write fractions with like denominators and solve fraction problems using the four operations.
Step It Out
1. Tom is running an obstacle course. Monkey bars make up \(\frac{1}{4}\) of the course, and hurdles make up \(\frac{1}{3}\) of the course. A wall climb and sprint make up the rest. What fraction of the course do the monkey bars and the hurdles make up?
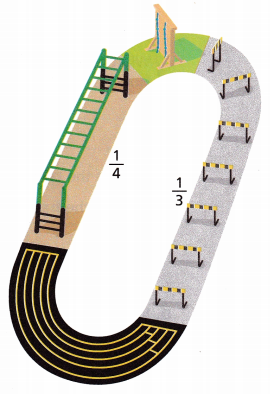
A. What operation do you need to use to solve this problem? How do you know?
__________________
___________________
Answer: Addition operation is used to solve this problem.
B. How is the least common multiple used when adding fractions with unlike denominators?
___________________
___________________
Answer:
Given,
Tom is running an obstacle course. Monkey bars make up \(\frac{1}{4}\) of the course, and hurdles make up \(\frac{1}{3}\) of the course.
\(\frac{1}{4}\) + \(\frac{1}{3}\)
The least common multiple of 3 and 4 is 12.
C. What is the LCM of the two denominators? How do you know?
___________________
Answer: LCM of 3 and 4 is 12.
D. Rewrite \(\frac{1}{4}\) using the LCM of 3 and 4.
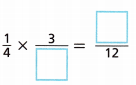
Answer:
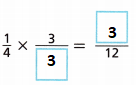
E. Rewrite \(\frac{1}{3}\) using the LCM of 3 and 4.
Answer:
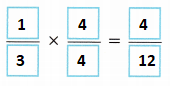
F. Write and evaluate an expression to find the fraction of the course the monkey bars and hurdles make up together.
Answer:
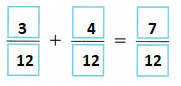
Turn and Talk Is there another way to solve this problem? Explain.
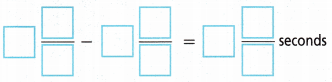
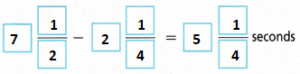
2. Tina takes 2\(\frac{1}{4}\) fewer seconds to finish the hurdles than to complete the monkey bars. How long does Tina take to finish the hurdles?

A. What operation do you need to use to solve this problem? How do you know?
______________________
______________________
Answer: The subtraction operation is used to solve this problem.
B. What is the LCM of the denominators in this problem? ______________________
Answer: The LCM of the denominator is 2 and 4 is 4.
C. Rewrite the fractions using the LCM.
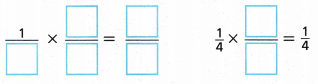
Answer:
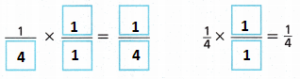
D. Write and evaluate an expression to find how long it takes Tina to complete the hurdles.
Answer:
Explanation:
Rewriting our equation with parts separated
7 + \(\frac{1}{2}\) – 2 – \(\frac{1}{4}\)
Solving the whole number parts
7 – 2 = 5
Solving the fraction parts
\(\frac{1}{2}\) – \(\frac{1}{4}\) = \(\frac{1}{4}\)
5 + \(\frac{1}{4}\) = 5 \(\frac{1}{4}\)
3. Davon spent \(\frac{2}{15}\) of his savings on a video game. He then spent 6\(\frac{1}{4}\) times as much on a bike. What fraction of his original savings did he spend on the bike?
A. What operation do you need to use to solve this problem? Explain.
______________________
______________________
Answer: Multiplication operation is used to solve the problem.
B. To multiply a fraction and a mixed number, convert ____ from a ___ to a ____.
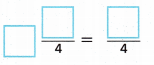
Answer:
To multiply a fraction and a mixed number, convert the fraction from a mixed to an improper fraction
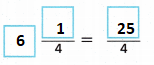
C. Write and evaluate an expression to find the fraction of his savings Davon spent on his bike. Use the GCF to write your answer in simplest form.
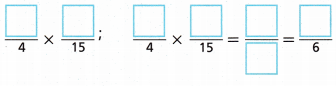
Answer:
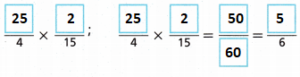
Turn and Talk Explain how you used the GCF to write your answer in Part C of Task 3 in simplest form.
4. On Saturday, Pedro has 3\(\frac{1}{2}\) hours to practice on an obstacle course. If it takes him \(\frac{1}{4}\) hour to complete the course, how many times can he go through the course in 3\(\frac{1}{2}\) hours?
A. Write a division expression to represent this situation.
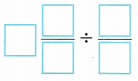
Answer:
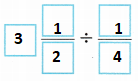
B. Evaluate the division expression using the reciprocal of the divisor. Show your work.
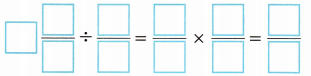
Answer:
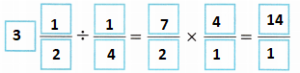
C. Explain how you can use the GCF to write your answer from Part B in simplest form.
__________________________
D. How many times can Pedro complete the obstacle course?
__________________________
Answer: 14 times can Pedro complete the obstacle course.
Check Understanding
Question 1.
At college, Tyrell has science for 5\(\frac{1}{2}\) hours per week. If his lab work takes up \(\frac{2}{5}\) of his science class time, how many hours does Tyrell spend in the lab?

Answer:
Given,
Tyrell has science for 5\(\frac{1}{2}\) hours per week.
His lab work takes up \(\frac{2}{5}\) of his science class time
5\(\frac{1}{2}\) × \(\frac{2}{5}\)
Convert from mixed fraction to improper fraction
5\(\frac{1}{2}\) = \(\frac{11}{2}\)
\(\frac{11}{2}\) × \(\frac{2}{5}\) = \(\frac{11}{5}\)
\(\frac{11}{5}\) = 2 \(\frac{1}{5}\) hours
Question 2.
Lena played two piano pieces at a recital. One piece was 5\(\frac{1}{2}\) minutes long. The other lasted 4\(\frac{2}{3}\) minutes. How long did Lena play during the recital? What operation did you use to solve the problem?
Answer:
Given,
Lena played two piano pieces at a recital. One-piece was 5\(\frac{1}{2}\) minutes long.
The other lasted 4\(\frac{2}{3}\) minutes.
5\(\frac{1}{2}\) + 4\(\frac{2}{3}\)minutes
Rewriting our equation with parts separated
5 + \(\frac{1}{2}\) + 4 + \(\frac{2}{3}\) minutes
Add the whole numbers
5 + 4 = 9
Add the fractions
\(\frac{1}{2}\) + \(\frac{2}{3}\)
LCD of 1/2 and 2/3 is 6
\(\frac{3}{6}\) + \(\frac{4}{6}\) = \(\frac{7}{6}\) = 1\(\frac{1}{6}\)
Now combine whole and fraction parts
9 + 1\(\frac{1}{6}\) = 10\(\frac{1}{6}\)
Question 3.
Sean is making fruit punch. He has 1\(\frac{5}{8}\) quarts of orange juice and 1\(\frac{2}{3}\) quarts of pineapple juice.
A. Write each amount using the LCM. ___________
Answer:
Sean is making fruit punch. He has 1\(\frac{5}{8}\) quarts of orange juice and 1\(\frac{2}{3}\) quarts of pineapple juice.
LCM of 8 and 3 is 24.
B. If Sean uses all of the juice he has, how much punch can he make?
____________________
Answer:
1\(\frac{5}{8}\) + 1\(\frac{2}{3}\)
Rewriting our equation with parts separated
1 + \(\frac{5}{8}\) + 1 + \(\frac{2}{3}\)
Solving the whole number parts
1 + 1 = 2
\(\frac{5}{8}\) + \(\frac{2}{3}\)
\(\frac{15}{24}\) + \(\frac{16}{24}\) = \(\frac{31}{24}\)
\(\frac{31}{24}\) = 1 \(\frac{7}{24}\)
2 + 1 + \(\frac{7}{24}\) = 3\(\frac{7}{24}\)
For Problems 4-6, perform the operation shown.
Question 4.
2\(\frac{2}{5}\) ÷ 3\(\frac{1}{5}\) __________________
Answer:
Given,
2\(\frac{2}{5}\) ÷ 3\(\frac{1}{5}\)
Convert from mixed fraction to the improper fraction.
2\(\frac{2}{5}\) = \(\frac{12}{5}\)
3\(\frac{1}{5}\) = \(\frac{16}{5}\)
\(\frac{12}{5}\) ÷ \(\frac{16}{5}\)
\(\frac{12}{5}\) × \(\frac{5}{16}\) = \(\frac{12}{16}\) = \(\frac{3}{4}\)
Question 5.
3\(\frac{3}{5}\) × 2\(\frac{1}{2}\) __________________
Answer:
Given,
3\(\frac{3}{5}\) × 2\(\frac{1}{2}\)
Convert from mixed fraction to the improper fraction.
3\(\frac{3}{5}\) = \(\frac{18}{5}\)
2\(\frac{1}{2}\) = \(\frac{5}{2}\)
\(\frac{18}{5}\) × \(\frac{5}{2}\) = \(\frac{18}{2}\) = 9
Question 6.
3\(\frac{1}{6}\) + 2\(\frac{5}{9}\) __________________
Answer:
Given,
3\(\frac{1}{6}\) + 2\(\frac{5}{9}\)
Convert from mixed fraction to the improper fraction.
First add the whole numbers
3 + 2 = 5
Now add the fractions
\(\frac{1}{6}\) + \(\frac{5}{9}\)
LCM of 6 and 9 is 18
\(\frac{3}{10}\) + \(\frac{10}{18}\) = \(\frac{13}{18}\) = 5\(\frac{13}{18}\)
On Your Own
Question 7.
There are 12 miles of hiking trails in a state park. Each trail is rated for difficulty: \(\frac{3}{8}\) of the trails are rated easy, \(\frac{1}{6}\) are rated moderate, \(\frac{1}{4}\) are rated hard, and \(\frac{5}{24}\) are rated difficult. What fraction of the trails are rated easy or moderate?
Answer:
Given,
There are 12 miles of hiking trails in a state park.
Each trail is rated for difficulty: \(\frac{3}{8}\) of the trails are rated easy, \(\frac{1}{6}\) are rated moderate, \(\frac{1}{4}\) are rated hard, and \(\frac{5}{24}\) are rated difficult.
To find a fraction of the trails are rated easy or moderate
\(\frac{3}{8}\) + \(\frac{1}{6}\)
LCM of 8 and 6 is 24
\(\frac{3}{8}\) + \(\frac{1}{6}\) = \(\frac{9}{24}\) + \(\frac{4}{24}\) = \(\frac{13}{24}\)
Question 8.
Terri peeled 2\(\frac{1}{6}\) pounds of potatoes for a stew. How many more pounds of potatoes does she need to peel so she peels 3\(\frac{3}{4}\) pounds of potatoes all together? What operation could you use to solve this problem?

Answer:
Given,
Terri peeled 2\(\frac{1}{6}\) pounds of potatoes for a stew.
To know how many more pounds of potatoes does she need to peel so she peels 3\(\frac{3}{4}\) pounds of potatoes all together we need to use the subtraction operation.
3\(\frac{3}{4}\) – 2\(\frac{1}{6}\)
3\(\frac{3}{4}\) – 2\(\frac{1}{6}\)
Rewriting our equation with parts separated
3 + \(\frac{3}{4}\) – 2 – \(\frac{1}{6}\)
3 – 2 = 1
\(\frac{3}{4}\) – \(\frac{1}{6}\)
LCM of 4 and 6 is 12
\(\frac{9}{12}\) – \(\frac{2}{12}\) = \(\frac{7}{12}\)
1 + \(\frac{7}{12}\) = 1\(\frac{7}{12}\)
Question 9.
Attend to Precision Agatha drives 73\(\frac{1}{2}\) miles through two towns in 2\(\frac{1}{3}\) hours. What is her average speed in miles per hour? Show how you know.
Answer:
Given,
Agatha drives 73\(\frac{1}{2}\) miles through two towns in 2\(\frac{1}{3}\) hours.
Division operation is used to find the average speed in miles per hour.
73\(\frac{1}{2}\) ÷ 2\(\frac{1}{3}\) hours
Convert from mixed fraction to the improper fraction.
73\(\frac{1}{2}\) = \(\frac{147}{2}\)
2\(\frac{1}{3}\) = \(\frac{7}{3}\)
\(\frac{147}{2}\) × \(\frac{3}{7}\) = \(\frac{441}{14}\) = 31 \(\frac{1}{2}\) hours
Question 10.
Roy, Joseph, and Caitlyn have 3\(\frac{3}{4}\) pints of chicken soup.
A. If they each eat the same amount of soup, how many pints will each person eat?
__________________________
Answer:
3\(\frac{3}{4}\) ÷ 3
Convert from mixed fraction to the improper fraction.
3\(\frac{3}{4}\) = \(\frac{15}{4}\)
\(\frac{15}{4}\) ÷ 3 = \(\frac{15}{4}\) × \(\frac{1}{3}\) = \(\frac{15}{12}\) = 1\(\frac{1}{4}\)
B. If they decide to include one more of their friends, how many pints will each person eat?
Answer:
If they include one more friend then it becomes 4 and we have to divide 3\(\frac{3}{4}\) by 4.
3\(\frac{3}{4}\) ÷ 4
Convert from mixed fraction to the improper fraction.
3\(\frac{3}{4}\) = \(\frac{15}{4}\)
\(\frac{15}{4}\) ÷ 4 = \(\frac{15}{4}\) × \(\frac{1}{4}\) = \(\frac{15}{16}\)
For Problems 11-14, perform the given operation on 4\(\frac{4}{5}\) and 2\(\frac{1}{2}\).
Question 11.
4\(\frac{4}{5}\) – 2\(\frac{1}{2}\) ______________
Answer:
Given,
4\(\frac{4}{5}\) – 2\(\frac{1}{2}\)
Rewriting our equation with parts separated
4 + \(\frac{4}{5}\) – 2 – \(\frac{1}{2}\)
Solving the whole number parts
4 – 2 = 2
Solving the fraction parts
\(\frac{4}{5}\) – \(\frac{1}{2}\)
LCD of 5 and 2 is 10.
\(\frac{8{10}\) – \(\frac{5}{10}\) = \(\frac{3}{10}\)
2 + \(\frac{3}{10}\) = 2\(\frac{3}{10}\)
Question 12.
4\(\frac{4}{5}\) × 2\(\frac{1}{2}\) ___________
Answer:
Given,
4\(\frac{4}{5}\) × 2\(\frac{1}{2}\)
Convert from mixed fraction to the improper fraction.
\(\frac{24}{5}\) × \(\frac{5}{2}\) = \(\frac{24×5}{5×2}\) = \(\frac{120}{10}\) = 2
Question 13.
4\(\frac{4}{5}\) ÷ 2\(\frac{1}{2}\) ___________
Answer:
Given,
4\(\frac{4}{5}\) ÷ 2\(\frac{1}{2}\)
Convert from mixed fraction to the improper fraction.
\(\frac{24}{5}\) × \(\frac{2}{5}\) = \(\frac{24×2}{5×5}\) = \(\frac{48}{25}\) = 1\(\frac{23}{25}\)
Question 14.
4\(\frac{4}{5}\) + 2\(\frac{1}{2}\) ___________
Answer:
Given
4\(\frac{4}{5}\) + 2\(\frac{1}{2}\)
Rewriting our equation with parts separated
4 + \(\frac{4}{5}\) + 2 + \(\frac{1}{2}\)
Solving the whole number parts
4 + 2 = 6
Add the fractions
\(\frac{4}{5}\) + \(\frac{1}{2}\)
LCD of 5 and 2 is 10.
\(\frac{8}{10}\) + \(\frac{5}{10}\) = \(\frac{13}{10}\) = 1\(\frac{3}{10}\)
6 + 1 + \(\frac{3}{10}\) = 7 \(\frac{3}{10}\)
Question 15.
A wail is 56\(\frac{1}{2}\) feet long. The art club will paint different murals that are each 14\(\frac{1}{8}\) feet long along the wall. How many murals will fit on the wall?
Answer:
Given,
A wail is 56\(\frac{1}{2}\) feet long. The art club will paint different murals that are each 14\(\frac{1}{8}\) feet long along the wall.
56\(\frac{1}{2}\) ÷ 14\(\frac{1}{8}\)
Convert from mixed fraction to the improper fraction.
56\(\frac{1}{2}\) = \(\frac{113}{2}\)
14\(\frac{1}{8}\) = \(\frac{113}{8}\)
\(\frac{113}{2}\) ÷ \(\frac{113}{8}\)
\(\frac{113}{2}\) × \(\frac{8}{113}\) = \(\frac{113×8}{2×113}\) = \(\frac{904}{226}\) = 4
Therefore 4 murals will fit on the wall.
Question 16.
Attend to Precision Patty rides her bike 2\(\frac{3}{4}\) miles to school. She rides 3\(\frac{5}{6}\) miles to get back home because she needs to meet her brother at his school first. How many miles does Patty ride her bike? Explain how you know that your answer is reasonable.

Answer:
Given,
Patty rides her bike 2\(\frac{3}{4}\) miles to school.
She rides 3\(\frac{5}{6}\) miles to get back home because she needs to meet her brother at his school first.
Addition operation is used to find how many miles Patty ride her bike.
2\(\frac{3}{4}\) + 3\(\frac{5}{6}\)
Rewriting our equation with parts separated
2 + \(\frac{3}{4}\) + 3 + \(\frac{5}{6}\)
2 + 3 = 5
\(\frac{3}{4}\) + \(\frac{5}{6}\)
LCD of 4 and 6 is 12.
\(\frac{9}{12}\) + \(\frac{10}{12}\) = \(\frac{19}{12}\)
\(\frac{19}{12}\) = 1 \(\frac{7}{12}\)
5 + 1 \(\frac{7}{12}\) = 6 \(\frac{7}{12}\)
Question 17.
William runs 6\(\frac{1}{5}\) miles daily. One day he runs 2\(\frac{1}{2}\) times as far as that. How many miles does he run that day?
Answer:
Given,
William runs 6\(\frac{1}{5}\) miles daily. One day he runs 2\(\frac{1}{2}\) times as far as that.
6\(\frac{1}{5}\) × 2\(\frac{1}{2}\)
Convert from mixed fraction to the improper fraction.
6\(\frac{1}{5}\) = \(\frac{31}{5}\)
2\(\frac{1}{2}\) = \(\frac{5}{2}\)
\(\frac{31}{5}\) × \(\frac{5}{2}\) = \(\frac{31}{2}\) = 15 \(\frac{1}{2}\)
Thus he runs 15 \(\frac{1}{2}\) miles that day.
Question 18.
Music A note represents the pitch and duration of a musical sound. In a four/four measure, a whole note is equal to two half notes, four quarter notes, or eight eighth notes. In a given measure, a composer wants to divide a half note into sixteenth notes. How many sixteenth notes should be used? Write and evaluate an expression to answer the question.
Answer:
Given, a whole note is equal to two half notes, four quarter notes, or eight eighth notes.
A half note into sixteenth notes
1.5 × 16 = 24
Question 19.
Reason Alex is setting up an inline skating course 21 feet long to practice weaving around cones. He wants a cone every 3\(\frac{1}{2}\) feet, but not at the start or end of the course. How many cones will he need? Explain your reasoning.
Answer:
Given,
Alex is setting up an inline skating course 21 feet long to practice weaving around cones.
He wants a cone every 3\(\frac{1}{2}\) feet, but not at the start or end of the course.
21 ÷ 3\(\frac{1}{2}\)
Convert from mixed fraction to the improper fraction
3\(\frac{1}{2}\) = \(\frac{7}{2}\)
21 × \(\frac{2}{7}\) = 3 × 2 = 6
Thus ne need 6 cones.
For Problems 20-23, perform the indicated operation.
Question 20.
7\(\frac{1}{2}\) – \(\frac{3}{4}\) ___________
Answer:
7\(\frac{1}{2}\) – \(\frac{3}{4}\)
Rewriting our equation with parts separated
7 + \(\frac{1}{2}\) – \(\frac{3}{4}\)
\(\frac{1}{2}\) – \(\frac{3}{4}\)
LCD of 2 and 4 is 4.
\(\frac{2}{4}\) – \(\frac{3}{4}\) = –\(\frac{1}{4}\)
7 –\(\frac{1}{4}\) = 6\(\frac{3}{4}\)
Question 21.
2\(\frac{2}{5}\) + 2\(\frac{1}{8}\) ___________
Answer:
2\(\frac{2}{5}\) + 2\(\frac{1}{8}\)
Rewriting our equation with parts separated
2 + \(\frac{2}{5}\) + 2 + \(\frac{1}{8}\)
Solving the whole number parts
2 + 2 = 4
Solving the fraction parts
\(\frac{2}{5}\) + \(\frac{1}{8}\)
LCD of 5 and 8 is 40
\(\frac{2}{5}\) + \(\frac{1}{8}\) = \(\frac{16}{40}\) + \(\frac{5}{40}\) = \(\frac{21}{40}\)
4 + \(\frac{21}{40}\) = 4\(\frac{21}{40}\)
Question 22.
\(\frac{1}{4}\) × 1\(\frac{3}{5}\) ___________
Answer:
\(\frac{1}{4}\) × 1\(\frac{3}{5}\)
Convert from mixed fraction to the improper fraction
1\(\frac{3}{5}\) = \(\frac{8}{5}\)
\(\frac{1}{4}\) × \(\frac{8}{5}\) = \(\frac{8}{20}\) = \(\frac{2}{5}\)
Question 23.
4\(\frac{1}{3}\) ÷ 1\(\frac{2}{3}\) ___________
Answer:
Given,
4\(\frac{1}{3}\) ÷ 1\(\frac{2}{3}\)
Convert from mixed fraction to the improper fraction
\(\frac{13}{3}\) ÷ \(\frac{5}{3}\)
\(\frac{13}{3}\) × \(\frac{3}{5}\) = \(\frac{39}{15}\)
Convert from improper fraction to the mixed fraction
\(\frac{39}{15}\) = 2 \(\frac{3}{5}\)
Question 24.
Beth participated in a triathlon that consisted of swimming, bicycling, and running. Her finishing time is shown below. If she completed the swimming portion in 1\(\frac{1}{4}\) hours and the bicycling portion in 6\(\frac{1}{3}\) hours, how long did it take her to complete the running portion of the triathlon?

Answer:
12 \(\frac{2}{3}\) – 1\(\frac{1}{4}\) – 6\(\frac{1}{3}\)
12 + \(\frac{2}{3}\) – 1 – \(\frac{1}{4}\) – 6 – \(\frac{1}{3}\)
(12 – 1) + \(\frac{2}{3}\) – \(\frac{1}{4}\) – (6 + \(\frac{1}{3}\))
11 + \(\frac{2}{3}\) – \(\frac{1}{4}\) – (6 + \(\frac{1}{3}\))
(11 – 6) + (\(\frac{2}{3}\) – \(\frac{1}{3}\)) – \(\frac{1}{4}\)
5 + (\(\frac{2}{3}\) – \(\frac{1}{3}\)) – \(\frac{1}{4}\)
5 + \(\frac{1}{3}\) – \(\frac{1}{4}\)
\(\frac{60}{12}\) + \(\frac{4}{12}\) – \(\frac{3}{12}\)
\(\frac{60+4-3}{12}\) = \(\frac{61}{12}\)
Question 25.
Construct Arguments Raja claims that to add two fractions with unlike denominators, first you need to determine the smallest number that is a multiple of both denominators. Then change the denominators in both fractions and keep the numerators the same. What is incorrect about his claim?
Answer: The answer is incorrect because to add two fractions that have unlike denominators, it is true that you first need to find a common denominator. When you change the denominator of a fraction you must also change its numerator in proportion to the change in the denominator.
Question 26.
A recipe for bread calls for 3\(\frac{1}{2}\) cups of flour, \(\frac{1}{8}\) cup of salt, and 1\(\frac{1}{4}\) cups of milk. What is the total amount of the three ingredients? Explain the process you used to answer the question and how you used the LCM.
Answer:
Given,
A recipe for bread calls for 3\(\frac{1}{2}\) cups of flour, \(\frac{1}{8}\) cup of salt, and 1\(\frac{1}{4}\) cups of milk.
3\(\frac{1}{2}\) + \(\frac{1}{8}\) + 1\(\frac{1}{4}\)
Rewriting our equation with parts separated
3 + \(\frac{1}{2}\) + \(\frac{1}{8}\) + 1 + \(\frac{1}{4}\)
Solving the whole number parts
3 + 1 = 4
Solving fractions
\(\frac{1}{2}\) + \(\frac{1}{8}\) + \(\frac{1}{4}\)
\(\frac{3}{4}\) + \(\frac{1}{8}\)
LCD of 4 and 8
\(\frac{6}{8}\) + \(\frac{1}{8}\) = \(\frac{7}{8}\)
Question 27.
A gasoline tank holds 12\(\frac{1}{2}\) gallons of gasoline. If there are 5\(\frac{1}{5}\) gallons of gasoline in the tank, how many more gallons can it hold?
__________________
Answer:
Given,
A gasoline tank holds 12\(\frac{1}{2}\) gallons of gasoline.
There are 5\(\frac{1}{5}\) gallons of gasoline in the tank.
12\(\frac{1}{2}\) – 5\(\frac{1}{5}\)
Rewriting our equation with parts separated
12 + \(\frac{1}{2}\) – 5 – \(\frac{1}{5}\)
12 – 5 = 7
\(\frac{1}{2}\) – \(\frac{1}{5}\)
LCD of 2 and 5 is 10.
\(\frac{1}{2}\) – \(\frac{1}{5}\)
\(\frac{5}{10}\) – \(\frac{2}{10}\) = \(\frac{3}{10}\)
7 + \(\frac{3}{10}\) = 7\(\frac{3}{10}\)
For Problems 28-30, perform the indicated operation.
Question 28.
5\(\frac{1}{3}\) – \(\frac{2}{9}\)
Answer:
5\(\frac{1}{3}\) – \(\frac{2}{9}\)
Rewriting our equation with parts separated
5 + \(\frac{1}{3}\) – \(\frac{2}{9}\)
\(\frac{1}{3}\) – \(\frac{2}{9}\)
LCD of 3 and 9 is 9.
\(\frac{3}{9}\) – \(\frac{2}{9}\) = \(\frac{1}{9}\)
5 + \(\frac{1}{9}\) = 5\(\frac{1}{9}\)
Question 29.
11\(\frac{2}{7}\) + 6\(\frac{1}{2}\)
Answer:
11\(\frac{2}{7}\) + 6\(\frac{1}{2}\)
Rewriting our equation with parts separated
11 + \(\frac{2}{7}\) + 6 + \(\frac{1}{2}\)
Solving the whole number parts
11 + 6 = 17
\(\frac{2}{7}\) + \(\frac{1}{2}\)
LCD of 7 and 2 is 14.
\(\frac{4}{14}\) + \(\frac{7}{14}\) = \(\frac{11}{14}\)
17 + \(\frac{11}{14}\) = 17\(\frac{11}{14}\)
Question 30.
2\(\frac{1}{2}\) ÷ \(\frac{3}{4}\) ___________
Answer:
2\(\frac{1}{2}\) ÷ \(\frac{3}{4}\)
Convert from mixed fraction to the improper fraction
2\(\frac{1}{2}\) = \(\frac{5}{2}\)
\(\frac{5}{2}\) ÷ \(\frac{3}{4}\)
\(\frac{5}{2}\) × \(\frac{4}{3}\) = \(\frac{20}{6}\) = 3 \(\frac{1}{3}\)
2\(\frac{1}{2}\) ÷ \(\frac{3}{4}\) = 3 \(\frac{1}{3}\)
Lesson 3.5 More Practice/Homework
Practice Fraction Operations
Question 1.
Renee worked a total of 16-\(\frac{1}{5}\) hours last week. She spent \(\frac{1}{3}\) of that time reviewing reports. How many hours did she spend reviewing reports?
Answer:
Given,
Renee worked a total of 16-\(\frac{1}{5}\) hours last week.
She spent \(\frac{1}{3}\) of that time reviewing reports.
16 \(\frac{1}{5}\) × \(\frac{1}{3}\)
Convert from mixed fraction to the improper fraction
16 \(\frac{1}{5}\) = \(\frac{81}{5}\)
\(\frac{81}{5}\) × \(\frac{1}{3}\) = \(\frac{81}{15}\) = 5\(\frac{2}{5}\)
Question 2.
Alisha added 5\(\frac{1}{4}\) quarts of water and 4\(\frac{2}{5}\) quarts of a cleaning solution to a large bucket. How much total liquid did she add to the bucket? Show your work.
Answer:
Given,
Alisha added 5\(\frac{1}{4}\) quarts of water and 4\(\frac{2}{5}\) quarts of a cleaning solution to a large bucket.
5\(\frac{1}{4}\) + 4\(\frac{2}{5}\)
Rewriting our equation with parts separated
5 + \(\frac{1}{4}\) + 4 + \(\frac{2}{5}\)
Solving the whole number parts
5 + 4 = 9
Solving the fraction parts
\(\frac{1}{4}\) + \(\frac{2}{5}\)
LCD of 4 and 5 is 20
\(\frac{5}{20}\) + \(\frac{8}{20}\) = \(\frac{13}{20}\)
9 + \(\frac{13}{20}\) = 9\(\frac{13}{20}\)
Question 3.
Math on the Spot Find the value of the expression. Write the answer in simplest form.
\(\frac{5}{12}\) – \(\frac{1}{10}\)
__________________
Answer:
\(\frac{5}{12}\) – \(\frac{1}{10}\)
LCD of 12 and 10 is 60
\(\frac{25}{60}\) – \(\frac{6}{60}\) = \(\frac{19}{60}\)
Question 4.
Kyle runs 3\(\frac{1}{4}\) miles in 22\(\frac{3}{4}\) minutes. He runs each mile in the same number of minutes. How many minutes does it take Kyle to run a mile?
Answer:
Given,
Kyle runs 3\(\frac{1}{4}\) miles in 22\(\frac{3}{4}\) minutes. He runs each mile in the same number of minutes.
22\(\frac{3}{4}\) ÷ 3\(\frac{1}{4}\)
Convert from mixed fraction to the improper fraction
22\(\frac{3}{4}\) = \(\frac{91}{4}\)
13\(\frac{1}{4}\) = \(\frac{13}{4}\)
\(\frac{91}{4}\) ÷ \(\frac{13}{4}\)
\(\frac{91}{4}\) × \(\frac{4}{13}\) = \(\frac{364}{52}\) = 7
Question 5.
Mary buys a bag of nuts that weighs 2\(\frac{1}{4}\) pounds. After a week, she has eaten \(\frac{2}{3}\) of the nuts. How many pounds of nuts has she eaten?
____________________
Answer:
Given,
Mary buys a bag of nuts that weighs 2\(\frac{1}{4}\) pounds.
After a week, she has eaten \(\frac{2}{3}\) of the nuts.
2\(\frac{1}{4}\) × \(\frac{2}{3}\)
Convert from mixed fraction to the improper fraction
2\(\frac{1}{4}\) = \(\frac{9}{4}\)
\(\frac{9}{4}\) × \(\frac{2}{3}\) = \(\frac{18}{12}\) = 1\(\frac{1}{2}\)
For Problems 6-11, perform the indicated operation.
Question 6.
5\(\frac{3}{4}\) + \(\frac{1}{10}\) ___________
Answer:
5\(\frac{3}{4}\) + \(\frac{1}{10}\)
Rewriting our equation with parts separated
5 + \(\frac{3}{4}\) + \(\frac{1}{10}\)
\(\frac{3}{4}\) + \(\frac{1}{10}\)
LCD of 4 and 10 is 20
\(\frac{15}{20}\) + \(\frac{2}{20}\) = \(\frac{17}{20}\)
5 + \(\frac{17}{20}\) = 5\(\frac{17}{20}\)
Question 7.
4\(\frac{3}{5}\) – 2\(\frac{1}{6}\) ___________
Answer:
4\(\frac{3}{5}\) – 2\(\frac{1}{6}\)
Rewriting our equation with parts separated
4 + \(\frac{3}{5}\) – 2 – \(\frac{1}{6}\)
Solving the whole number parts
4 – 2 = 2
Solving the fraction parts
\(\frac{3}{5}\) – \(\frac{1}{6}\)
LCD of 5 and 6 is 30.
\(\frac{18}{30}\) – \(\frac{5}{30}\) = \(\frac{13}{30}\)
2 + \(\frac{13}{30}\) = 2\(\frac{13}{30}\)
Question 8.
5\(\frac{1}{3}\) × 2\(\frac{4}{5}\) ___________
Answer:
5\(\frac{1}{3}\) × 2\(\frac{4}{5}\)
Convert from mixed fraction to the improper fraction
5\(\frac{1}{3}\) = \(\frac{16}{3}\)
2\(\frac{4}{5}\) = \(\frac{14}{5}\)
\(\frac{16}{3}\) × \(\frac{14}{5}\) = \(\frac{224}{15}\) = 14 \(\frac{14}{15}\)
Question 9.
4\(\frac{1}{2}\) ÷ 4\(\frac{5}{8}\) ___________
Answer:
4\(\frac{1}{2}\) ÷ 4\(\frac{5}{8}\)
Convert from mixed fraction to the improper fraction
4\(\frac{1}{2}\) = \(\frac{9}{2}\)
4\(\frac{5}{8}\) = \(\frac{37}{8}\)
\(\frac{9}{2}\) ÷ \(\frac{37}{8}\)
\(\frac{9}{2}\) × \(\frac{8}{37}\) = \(\frac{72}{74}\) = \(\frac{36}{7}\)
4\(\frac{1}{2}\) ÷ 4\(\frac{5}{8}\) = \(\frac{36}{7}\)
Question 10.
6\(\frac{1}{8}\) ÷ \(\frac{3}{16}\) ___________
Answer:
6\(\frac{1}{8}\) ÷ \(\frac{3}{16}\)
Convert from mixed fraction to the improper fraction
6\(\frac{1}{8}\) = \(\frac{49}{8}\)
\(\frac{49}{8}\) ÷ \(\frac{3}{16}\)
\(\frac{49}{8}\) × \(\frac{16}{3}\) = \(\frac{784}{24}\) = 32\(\frac{2}{3}\)
6\(\frac{1}{8}\) ÷ \(\frac{3}{16}\) = 32\(\frac{2}{3}\)
Question 11.
3\(\frac{4}{5}\) × 1\(\frac{2}{3}\) ___________
Answer:
3\(\frac{4}{5}\) × 1\(\frac{2}{3}\)
Convert from mixed fraction to the improper fraction
3\(\frac{4}{5}\) = \(\frac{19}{5}\)
1\(\frac{2}{3}\)= \(\frac{5}{3}\)
\(\frac{19}{5}\) × \(\frac{5}{3}\) = \(\frac{95}{15}\)
Now convert from improper fraction to the mixed fraction
\(\frac{95}{15}\) = 6 \(\frac{1}{3}\)
Test Prep
Question 12.
Andrea finished her homework in \(\frac{2}{3}\) the amount of time it took Dina to finish hers. Dina took 2\(\frac{4}{5}\) hours to finish her homework. Which expression shows how long Andrea took to finish her homework?
A. \(\frac{2}{3}\) + 2\(\frac{4}{5}\)
B. 2\(\frac{4}{5}\) – \(\frac{2}{3}\)
C. 2\(\frac{4}{5}\) ÷ \(\frac{2}{3}\)
D. \(\frac{2}{3}\) × 2\(\frac{4}{5}\)
Answer:
Given,
Andrea finished her homework in \(\frac{2}{3}\) the amount of time it took Dina to finish hers. Dina took 2\(\frac{4}{5}\) hours to finish her homework.
\(\frac{2}{3}\) × 2\(\frac{4}{5}\)
2\(\frac{4}{5}\) = \(\frac{14}{5}\)
\(\frac{2}{3}\) × \(\frac{14}{5}\) = \(\frac{28}{5}\) = 1\(\frac{13}{15}\)
Option D is the correct answer.
Question 13.
Which expression(s) have a value that is greater than 6? Select all that apply.
A. 6 – \(\frac{1}{5}\)
B. 6 × \(\frac{2}{3}\)
C. 6 × 2\(\frac{1}{8}\)
D. 6 – \(\frac{1}{20}\)
E. 6 ÷ \(\frac{3}{4}\)
Answer:
6 × \(\frac{2}{3}\) and 6 × 2\(\frac{1}{8}\) has value that is greater than 6.
Options B and C are correct answers.
Question 14.
Laurie is measuring crushed garlic for a recipe. Each serving requires \(\frac{3}{4}\) teaspoon of garlic. If Laurie has 2\(\frac{5}{8}\) teaspoons of garlic, how many servings can she make?
Answer:
Given,
Laurie is measuring crushed garlic for a recipe. Each serving requires \(\frac{3}{4}\) teaspoon of garlic.
Laurie has 2\(\frac{5}{8}\) teaspoons of garlic
2\(\frac{5}{8}\) ÷ \(\frac{3}{4}\)
Convert from mixed fraction to the improper fraction
2\(\frac{5}{8}\) = \(\frac{21}{8}\)
\(\frac{21}{8}\) ÷ \(\frac{3}{4}\)
\(\frac{21}{8}\) × \(\frac{4}{3}\) = 3 \(\frac{1}{2}\)
Question 15.
A hippo weighed \(\frac{1}{20}\) ton when it was born. When the hippo turned
10 years old, it weighed 1\(\frac{1}{2}\) tons. Which expression shows the number of tons the hippo’s weight increased between its birth and its tenth birthday?
A. 1\(\frac{1}{2}\) – \(\frac{1}{20}\)
B. \(\frac{1}{20}\) + 1\(\frac{1}{2}\)
C. 1\(\frac{1}{2}\) × \(\frac{1}{20}\)
D. \(\frac{1}{20}\) ÷ 1\(\frac{1}{2}\)
Answer:
A hippo weighed \(\frac{1}{20}\) ton when it was born.
When the hippo turned 10 years old, it weighed 1\(\frac{1}{2}\) tons.
Subtraction operation is used to solve this problem to show the number of tons the hippo’s weight increased between its birth and its tenth birthday
1\(\frac{1}{2}\) – \(\frac{1}{20}\)
Option A is the correct answer.
Spiral Review
Question 16.
What integer can be used to represent a diver’s elevation if the diver is 40 feet below sea level?
Answer: -40
Explanation:
Below 0 is a negative number
Below sea level of 40 feet is -40 feet
Question 17.
Add the decimals: 0.14 + 1.29.
Answer: 1.43
The sum of two decimals 0.14 and 1.29 is 1.43
Question 18.
What is the least common multiple of 18 and 27?
______________________
Answer:
The least common multiple of 18 and 27 is 54
To find the LCM of 18 and 27, we need to find the multiples of 18 and 27.
18 = 18, 36, 54, 72
27 = 27, 54, 81, 108