We included HMH Into Math Grade 6 Answer Key PDF Module 11 Lesson 4 Find Perimeter and Area on the Coordinate Plane to make students experts in learning maths.
HMH Into Math Grade 6 Module 11 Lesson 4 Answer Key Find Perimeter and Area on the Coordinate Plane
I Can find the perimeter and area of polygons in the coordinate plane.
Step It Out
You can use what you learned about finding the distance between points to find areas and perimeters of figures on the coordinate plane.
Question 1.
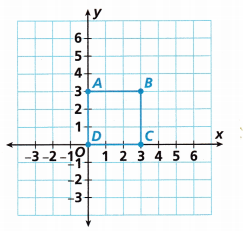
Find the perimeter of the rectangle on the city grid shown.
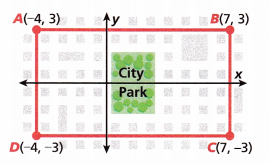
A. To find the perimeter of Rectangle ABCD, ___________ the lengths of the sides.
Answer:
The perimeter of the rectangle:
The perimeter of a rectangle is defined as the sum of all the sides of a rectangle. For any polygon, the perimeter formulas are the total distance around its sides. In the case of a rectangle, the opposite sides of a rectangle are equal and so, the perimeter will be twice the width of the rectangle plus twice the length of the rectangle and it is denoted by the alphabet “p”.
B. The coordinates of Point A are __________. The coordinates of Point B are ___________. The length of Side AB is ___________ units.
Answer:
The coordinates of point A are (-4, 3)
The coordinates of point B are (7,3)
The length of side AB is X.
X = 11 units.
count the squares between the points.
C. The coordinates of Point B are ___________. The coordinates of Point C are ___________. The length of Side BC is ___________ units.
Answer:
The coordinate points of B are (7, 3)
The coordinate points of C are (7, -3)
The length of side BC is Y units.
Now count the square between the points.
Y = 6 units.
D. The coordinates of Point C are ____________. The coordinates of Point D are _____________. The length of Side CD is __________ units.
Answer:
The coordinate of point C is (7, -3)
The coordinate points of D are (-4, -3)
The length of the side CD is Z units.
Now count the square between the points.
Z = 11 units.
E. The coordinates of Point D are _____________. The coordinates of Point A are ____________. The length of Side DA is ___________ units.
Answer:
The coordinate points of D are (-4, -3)
The coordinate points of A are (-4, 3)
The length of the side DA is P units.
Now count the squares between the points.
P = 8 units.
F. The perimeter of Rectangle ABCD is ![]() +
+ ![]() +
+ ![]() +
+ ![]() =
= ![]() units.
units.
Answer:
Since the perimeter is equal to the sum of all the sides of the polygon. Hence, in the case of a rectangle, the perimeter (P) is;
P = sum of all its four sides
P = a + b + a + b (Opposite sides of rectangle are equal)
Now add all the lengths and widths.
Perimeter = 11 + 6 + 11 + 8
Perimeter = 36 units.
Therefore, the perimeter of the rectangle ABCD is 36 units.
Turn and Talk Explain how you can find the perimeter of a rectangle on the coordinate plane without using the coordinates of the points.
Answer:
– Using the coordinate plane will help us find the perimeter and area of different shapes. You first draw the shape on the coordinate plane and then you can count the number of unit squares the shape takes up. For perimeter, it’s the number of unit squares that go around the shape.
Question 2.
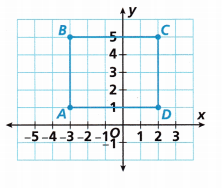
Recall that the formula for the area of a rectangle is A = b × h, where b is the length of the base and h is the height.
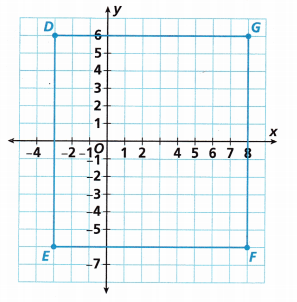
A. If we consider Side EF to be the base of the rectangle, which side’s length is the height?
Answer:
EF is the base of the rectangle.
ED is the height of the rectangle.
B. To find the length of the rectangle’s base, add the absolute value of the ___________ -coordinates of Point E and Point F: |![]() | + |
| + |![]() |
|
The length of the rectangle’s base is
![]() +
+ ![]() =
= ![]() units.
units.
Answer:
The coordinates of point E are (-3, -6)
The coordinates of point F are (8, -6)
The points are different quadrants with the same y-coordinates. So we can use the absolute values.
|-3| + |8| = 3 + 8 = 11 units.
Therefore, the length of the rectangle’s base is 11 units.
C. Count the units on the coordinate plane between Point E and Point F to check the length from Part B. Is the length correct? How many units did you count?
Answer:
– Now count the units in the coordinate plane as per the question asked.
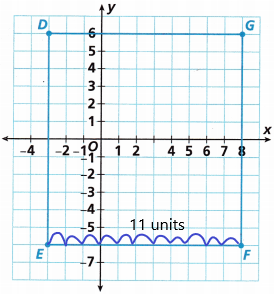
The length between point E and point F is 11 units.
Therefore, in part B what we calculated is correct.
Hence, we count 11 units in the coordinate plane.
D. To find the rectangle’s height, add the absolute value of the ___________ -coordinates of Point E and Point D: |![]() | + |
| + |![]() |.
|.
The rectangle’s height is ![]() +
+ ![]() =
= ![]() units.
units.
Answer:
The coordinates of point E are (-3, -6)
The coordinate of point D are (-3, 6)
The quadrants are different with the same x-coordinates. So we can use the absolute values.
|-6| + |6| = 6 + 6 = 12 units.
Therefore, the height of the rectangle is 12 units.
E. Count the units on the coordinate plane between Point E and Point D to check the length from Part D. Is the length correct? How many units did you count?
Answer:
– Now count the units in the coordinate plane as per the question asked.
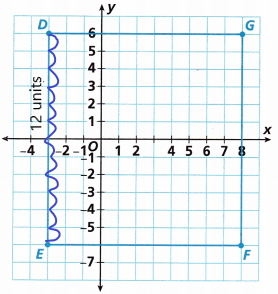
The length between point E and point D is 12 units.
Therefore, in part D what we calculated is correct.
Hence, we count 12 units in the coordinate plane.
F. Find the area of the rectangle.
A = b × h
= ![]() ×
× ![]()
= ![]() square units
square units
Answer:
The length of the rectangle = 11
The height of a rectangle = 12
Area of the rectangle = length x height
A = 11 x 12
A = 132 square units.
Turn and Talk What are two ways to find the area of a rectangle on a coordinate plane? Explain.
Answer:
– The two ways we can find the area of a rectangle are:
– One way is by using the formula a = l x h
– The other option, although quite tedious, would be to count all the squares inside the rectangle.
Question 3.
Alex is designing a rectangular piece of art. He uses the points (1, -1), (4, -1), (4, -8), and (1, -8) to draw the a rectangle on a coordinate plane to begin the piece.

A. Graph the points on the coordinate plane. Then connect the points in the order they were given to draw the rectangle.
Answer:
The above-given coordinate points are (1, -1), (4, -1), (4, -8), and (1, -8)
– Plot these vertices in the coordinate plane.
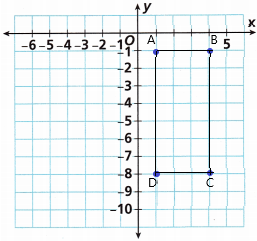
B. What are the length and width of the rectangle?
Answer:
The coordinate points of C are (4, -8)
The coordinate points of D are (1, -8)
The length of the rectangle is X.
The quadrants are the same with the same y-coordinates. So we can use the absolute values or we can count the squares.
|4| – |1| = |4-1| = 3 units.
X = 3 units
Therefore, the length of the rectangle is 3 units.
The coordinate points of A are (1, -1)
The coordinate points of D are (1, -8)
The width of the rectangle is Y.
The quadrants are the same with the same x-coordinates. So we can use the absolute values or we can count the squares.
|-8 – (-1)| = |-8 + 1| = 7 units
Y = 7 units.
Therefore, the width of the rectangle is 7 units.
C. Find the perimeter of the rectangle.
P = ![]() +
+ ![]() +
+ ![]() +
+ ![]() =
= ![]() units
units
Answer:
Since the perimeter is equal to the sum of all the sides of the polygon. Hence, in the case of a rectangle, the perimeter (P) is;
P = sum of all its four sides
P = a + b + a + b (Opposite sides of rectangle are equal)
P = 2 ( a+b)
Now add all the lengths and widths.
Perimeter = 2(3 + 7)
Perimeter = 2 (10)
Perimeter = 20 units
Therefore, the perimeter of the rectangle ABCD is 20 units
D. Find the area of the rectangle.
A = ![]() ×
× ![]() =
= ![]() square units
square units
Answer:
The length of the rectangle = 3
The width of a rectangle = 7
Area of the rectangle = length x width
A = 7 x 3
A = 21 square units.
Question 4.
Figures PQRS and TUVWare squares. Find the shaded area.
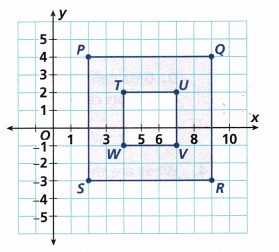
A. Find the length of side PS.
![]() +
+ ![]() =
= ![]() units
units
Answer:
The coordinate of point P(2, 4)
The coordinate of point S (2, -3)
The quadrants are different with the same x-coordinates. So we can use the absolute values.
|4 – (-3)| = 4 + 3 = 7 units
Therefore, the length of the side PS is 7 units.
(or)
we can count the squares also then also we get 7 units.
B. Find the length of side TW.
![]() +
+ ![]() =
= ![]() units
units
Answer:
The coordinate of point T (4, 2)
The coordinate of point W(4, -1)
The quadrants are different with the same x-coordinates. So we can use the absolute values.
|2 – (-1)| = 2 + 1 = 3 units
Therefore, the length of the side TW is 3 units.
(or)
we can count the squares also then also we get 3 units.
C. Find the shaded area.
Shaded area = Area of PQRS – Area of TUVW
= ![]() –
– ![]()
= ![]() –
– ![]()
= ![]() square units
square units
Answer:
The side of a PQRS = 7 units
The side of a TUVW = 3 units
Area of square = side x side
The area of PQRS = 7 x 7 = 49
The area of TUVW = 3 x 3 = 9
Now we have to find out the shaded area.
shaded area= 49 – 9
shaded area = 40 square units.
Check to understand
Question 1.
A blueprint of a rectangular pool is shown. What are the area and perimeter of the pool?
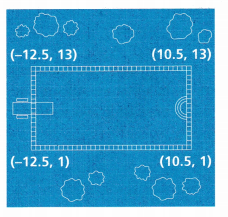
Answer:
The coordinates of point A (-12.5, 13)
The coordinate pf point B (10.5, 13)
The coordinate of point C is (10.5, 1)
The coordinate of point D (-12.5, 1)
The length of the rectangle is X.
The length of a rectangle CD.
The quadrants are different with the same y-coordinates. So we can use the absolute values.
|10.5 – (-12.5)| = |10.5 + 12.5| = 23 units.
X = 23 units.
The width of the rectangle is Y
The quadrants are different with the same X-coordinates. So we can use the absolute values.
The width of the rectangle BC
|13 – 1| = 12 units.
Y= 12 units
Therefore, the width of the rectangle is 12 units.
Question 2.
What is the area of a rectangle ABCD with vertices at A(-8, 5), B(-8, -4), C(3, -4), and D(3, 5)?
Answer:
The above-given vertices: A(-8, 5), B(-8, -4), C(3, -4), and D(3, 5)
To find the area of the rectangle, first, we need to find out the length and width of the rectangle.
The length of the rectangle CD
C(3, -4), and D(3, 5)
The quadrants are different with the same x-axis.
|-4 – 5| = |-9| = 9 units.
Therefore, the length of the rectangle is 9 units.
The width of the rectangle AD
A(-8, 5) and D(3, 5)
The quadrants are different with the same y-coordinates.
|-8 – 3| = |-11| = 11 units.
Therefore, the width of the rectangle is 11 units.
Now we can find out the area of the rectangle.
area = length x width
area = 9 x 11
area= 99 square units.
On Your Own
Question 3.
Gina is growing lettuce in a section of a garden. She represents this section with Rectangle JKLM. Each unit in the coordinate plane represents 1 foot.

A. What is the area of the section where lettuce grows?
A = ![]() ×
× ![]() =
= ![]() square feet
square feet
Answer:
We counted the squares to find out the length and the width.
The length of the lettuce plants = 5 units
The width of the lettuce plants = 2 units
Now we can find out the area of the section where lettuce grows.
area= l x w
area= 5 x 2
area = 10 square units.
B. Each head of lettuce needs a 2-foot-square region. How many heads of lettuce can Gina plant?
Answer:
The number of heads of lettuce can Gina plant = P
Each head needs a 2-foot-square region.
P = area x 2
P = 10 x 2
P = 20
Therefore, Gina can plant 20 heads of lettuce.
C. Gina decides to use a section of the lettuce region to plant carrots. Rectangle MNOP represents this section of the garden. Find the area of this section of the garden.
A = ![]() ×
× ![]() =
= ![]() square feet
square feet
Answer:
We counted the squares to find out the length and the width.
The length of the lettuce plants = 5 units
The width of the lettuce plants = 2 units
Now we can find out the area of the section where lettuce grows. And this region will be used to plant the carrots by Gina.
area= l x w
area= 5 x 2
area = 10 square units.
D. Gina can plant 8 carrots per square foot. How many carrots can Gina plant in the garden?
Answer:
The number of carrots Gina can plant per square foot = 8
The area = 10 square units.
The number of carrots Gina can plant = C
C = 10 x 8
C = 80
Therefore, she can plant 80 carrots in the garden.
Question 4.
What are the area and perimeter of the quadrilateral?
A. Graph the points (-4, -1), (-1, -1), (-1, -5), and (-4, -5) on the coordinate plane. Then connect the points in the order given.
Answer:
The above-given points: (-4, -1), (-1, -1), (-1, -5), and (-4, -5)
– Plot the points in the coordinate plane and connect the points.
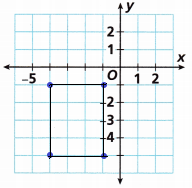
The polygon we got is a rectangle.
B. Find the perimeter of the quadrilateral.
P = ![]() +
+ ![]() +
+ ![]() +
+ ![]() =
= ![]() units
units
Answer:
We count the squares between the points.
The length of the rectangle = 4 units
The width of the rectangle = 3 units
Since the perimeter is equal to the sum of all the polygon sides. Hence, in the case of a rectangle, the perimeter (P) is;
P = sum of all its four sides
P = a + b + a + b (Opposite sides of rectangle are equal)
P = 2 ( a+b)
Now add all the lengths and widths.
Perimeter = 2(4 + 3)
Perimeter = 2 (7)
Perimeter = 14 units
Therefore, the perimeter of the rectangle ABCD is 14 units
C. Find the area of the quadrilateral.
A = ![]() ×
× ![]() =
= ![]() square units
square units
Answer:
The length of the rectangle = 4
The width of a rectangle = 3
Area of the rectangle = length x width
A = 4 x 3
A = 12 square units.
Question 5.
Reason The length of one rectangle in a quilt is 6 inches. Its width is 3 inches. About how many of these rectangles do you need to cover an area of 7,500 square inches? Explain.
Answer:
length = 6
width = 3
area = 7500
Perimeter = 2 (a + b)
Perimeter = 2(6 + 3)
Perimeter = 2(9)
Perimeter = 18
The number of rectangles do we need = X
X = 7500/18
X = 416.66 square inches
Question 6.
Use the figure on the coordinate plane.
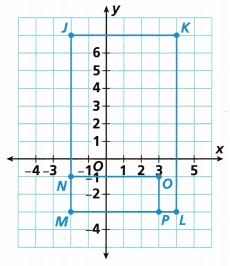
A. What is the area of Rectangle FGHK?
Answer:
We count the squares to know the length and the width.
The length of the rectangle = 9
The width of a rectangle = 6
Area of the rectangle = length x width
A = 9 x 6
A = 54 square units.
B. What is the area of Rectangle PQRS?
Answer:
We count the squares to know the length and the width.
The length of the rectangle = 5
The width of a rectangle = 4
Area of the rectangle = length x width
A = 5 x 4
A = 20 square units.
C. What is the area of the shaded region? Explain how you found your answer.
Answer:
We know that the area of the rectangle FGHK and the area of the rectangle PQRS
Subtract both the area to get the shaded region.
Shaded region = area of the rectangle FGHK – an area of the rectangle PQRS
Shaded region = 54 – 20
Shaded region= 34 square units.
Question 7.
Use Structure Wendy needs to make a sheet cake for a party. She draws a plan for the sheet cake on a coordinate plane. One piece of cake is shown in green.
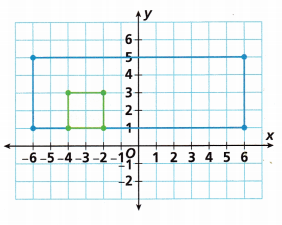
A. What is the perimeter of the sheet cake?
Answer:
We count the squares between the points.
The length of the rectangle = 12 units
The width of the rectangle = 4 units
Since the perimeter is equal to the sum of all the polygon sides. Hence, in the case of a rectangle, the perimeter (P) is;
P = sum of all its four sides
P = a + b + a + b (Opposite sides of rectangle are equal)
P = 2 ( a+b)
Now add all the lengths and widths.
Perimeter = 2(12 + 4)
Perimeter = 2 (16)
Perimeter = 32 units
Therefore, the perimeter of the rectangle ABCD is 32 units
B. What is the area of the sheet cake?
Answer:
We count the squares between the points.
The length of the rectangle = 12 units
The width of the rectangle = 4 units
area of the rectangle = length x width
area of the rectangle = 12 x 4 = 48 square units
Therefore, the area of the sheet cake is 48 square units.
C. Given the size of the first piece of cake cut from the sheet cake, can the cake be cut into pieces of the same size with no cake left over? Explain.

Answer: yes, we can cut the same size with no cake leftover.
The coordinate plane is shown below:
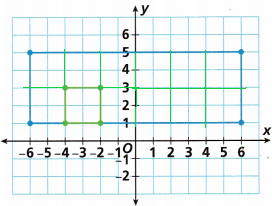
There are 4 rows and 12 columns
Firstly, the cake is cut into 4 squares. Likewise, we divided the cake throughout the sheet.
D. Open-Ended On the coordinate plane, draw two more ways to cut the cake so that the cake can be divided into equal pieces with nothing left over. Name how many people you can feed each time.
Answer:
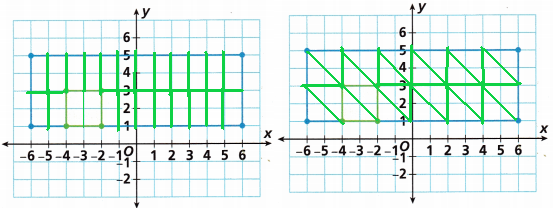
In the first coordinate plane, the cake is cut into a rectangular shape and we can feed 24 people each time.
In the second coordinate plane, the cake is cut into a triangular shape and we can feed 24 people each time.
Question 8.
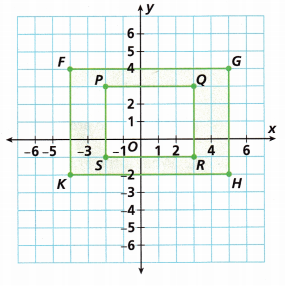
Look at the figure. Rectangles A and B partly cover Rectangle C.
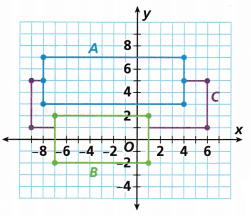
A. What is the outside perimeter of the entire figure?
Answer:
We count the squares between the points.
The length of the rectangle = 18 units
The width of the rectangle = 15 units
Since the perimeter is equal to the sum of all the polygon sides. Hence, in the case of a rectangle, the perimeter (P) is;
P = sum of all its four sides
P = a + b + a + b (Opposite sides of rectangle are equal)
P = 2 ( a+b)
Now add all the lengths and widths.
Perimeter = 2(18 + 15)
Perimeter = 2 (33)
Perimeter = 66 units
Therefore, the perimeter of the rectangle ABCD is 66 units
B. What is the area of Rectangle A?
Answer:
Count the squares of the rectangle A.
The length of rectangle A = 12 units
The width of the rectangle A = 4 units
area of the rectangle = length x width
area of the rectangle = 12 x 4 = 48 square units
Therefore, the area of rectangle A is 48 square units.
C. What is the area of Rectangle B?
Answer:
Count the squares of the rectangle B.
The length of rectangle A = 8 units
The width of the rectangle A = 4 units
area of the rectangle = length x width
area of the rectangle = 8 x 4 = 32 square units
Therefore, the area of rectangle B is 32 square units.
D. Attend to Precision What is the area of the part of Rectangle C that ¡s not covered by the other rectangles?
Answer:
The outside part we have to calculate.
The length is 7
the width is 4
area of the rectangle C = length x width
area of the rectangle C = 7 x 4 = 28 square units.
Therefore, the area of rectangle C is 28 square units.
Question 9.
Open-Ended Draw a rectangle on the coordinate plane with an area of 12 square units. What is the rectangle’s perimeter?
Answer:
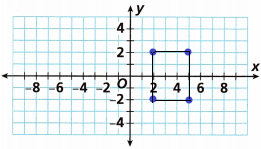
area of the rectangle = length x width
already given that, the area of the rectangle = 12 square units.
according to the area, we can find out the length and the width.
length = 4 units
width = 3 units
We need to find out the perimeter of the rectangle.
Perimeter of the rectangle = 2(l+w)
Perimeter of the rectangle = 2(4 + 3)
the perimeter of the rectangle = 2(7)
the perimeter of the rectangle = 14 square units.
Question 10.
The pattern for the two wings of a hang glider is shown on the grid. The unit is inches. What is the total area of the wings? What is the area of each wing?
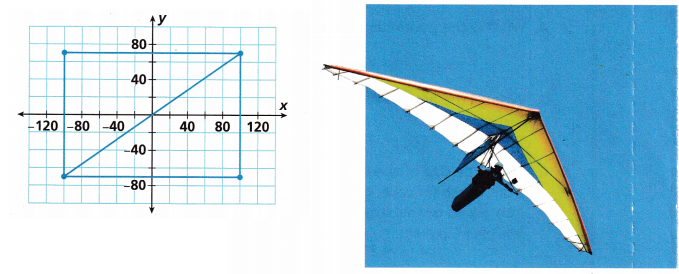
Answer:
Right angle triangle:
The area of a right triangle is the space occupied inside the boundary of the right triangle. Generally, the space inside the boundary is divided into squares of unit length. Hence, the number of unit squares that are present inside the right triangle is calculated as the area of a right triangle. The unit used to measure the area is the square unit.
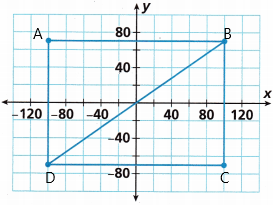
The coordinates are A(-100, 70) B(100, 70) C(100, -70) D(-100, -70)
To find out the area of each triangle, we need to know the formula for the area of the right triangle.
From the above-given figure, it is observed that a rectangle is divided into two right-angled triangles, and they are congruent to each other, such that one triangle overlaps the other triangle.
We know that, Area of a rectangle = Length × Width of square units
So, the area of the rectangle = 2 × (Area of one right triangle)
Thus, the Area of one right triangle = (½) × Area of rectangle = (½ ) × length × Width
Since, length = base (b) and width = height(h),
Now calculate the area for the triangle ABD
length of AB = |-100| – |100| = |-200| = 200
width of AD = |70| – |-70| = |70 + 70| = 140
area of one right triangle = 1/2 x 200 x 140
area of one triangle = 100 x 140 = 14000 square units.
Now calculate the areaof the triangle DCB
Length of DC = |-100| – |100| = |-200| = 200
width of BC = |70| – |-70| = |70 + 70| = 140
area of other right triangle = 1/2 x 200 x 140
area of other triangle = 100 x 140 = 14000 square units.
The total area is area of the triangle ABD + area of the triangle DCB
total area = 14000 + 14000
total area = 28000 square units.
The area of a right triangle = (½)×b×h square unit
Question 11.
What is the area of the rectangle shown on the coordinate plane?
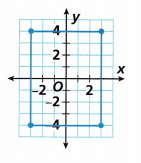
Answer:
We count the squares to know the length and the width.
The length of the rectangle = 8
The width of a rectangle = 6
Area of the rectangle = length x width
A = 8 x 6
A = 48 square units. (or else)
we can use the absolute values to find out the length and width. This process is shown above in the above questions.
Lesson 11.4 More Practice/Homework
For Problems 1-2, use the following information.
An engineer is tasked with doubling the length and width of a city park. The engineer draws the park on a coordinate plane and labels it ABCD.

Question 1.
Find the area of the park before and after the expansion.
A. What is the area of the park before the expansion?
Answer:
First, we have to calculate the area of the square ABCD which is before the length and width are doubled.
area of a square = side x side
The side length is 3.
p = 3 x 3
p = 9 square units.
Therefore, the area of the park before doubled is 9 square units.
B. What is the area of the park after the length and width is doubled?
Answer:
First, we have to calculate the area of the square ABCD which is after the length and width are doubled.
area of a square = side x side
The side length is 11.
p = 11 x 11
p = 121 square units.
Therefore, the area of the park after doubled is 121 square units.
C. By what factor did the area change?
Answer:
Changing a dimension will often have a greater effect on the figure’s area than it will on its perimeter. Even when the dimensions aren’t being squared in an area formula, they might be multiplied together, so a change in one dimension can have a significant effect on the area.
Question 2.
Find the perimeter of the park before and after the expansion.
A. What is the perimeter of the park before the length and width are doubled?
Answer:
First, we have to calculate the perimeter of the square ABCD which is before the length and width are doubled.
Perimeter of a square = a + a + a + a
p = 4a
The side length is 3.
p = 4 x 3
p = 12 units.
Therefore, the perimeter of the park before doubled is 12 units.
B. What is the perimeter of the park after the length and width is doubled?
Answer:
First, we have to calculate the perimeter of the square ABCD which is after the length and width are doubled.
Perimeter of a square = a + a + a + a
p = 4a
The side length is 11.
p = 4 x 11
p = 44 units.
Therefore, the perimeter of the park after doubled is 44 units.
C. By what factor did the perimeter change?
Answer:
Changing one of the dimensions, such as length or width, of a figure can have a significant impact on the figure’s perimeter (total length of the edge) and its area (size of the surface).
Question 3.
Math on the Spot What is the perimeter of the rectangle shown?
Answer:
We count the squares between the points.
The length of the rectangle = 5 units
The width of the rectangle = 4 units
Since the perimeter is equal to the sum of all the polygon sides. Hence, in the case of a rectangle, the perimeter (P) is;
P = sum of all its four sides
P = a + b + a + b (Opposite sides of rectangle are equal)
P = 2 ( a+b)
Now add all the lengths and widths.
Perimeter = 2(5 + 4)
Perimeter = 2 (9)
Perimeter = 18 units
Therefore, the perimeter of the rectangle ABCD is 18 units
For Problems 4-7, find the length of the segment with the given endpoints.
Question 4.
(-12, 4), (21, 4)
Answer:
On a graph, the length of a line segment can be found by using the distance formula, between its endpoints. Else, we can use a ruler to measure the length of smaller line segments too.
The above-given coordinates:
(-12, 4) and (21, 4)
A = (x1, y1) = (-12, 21)
B = (x2, y2) = (4, 4)
We can start with the distance formula:
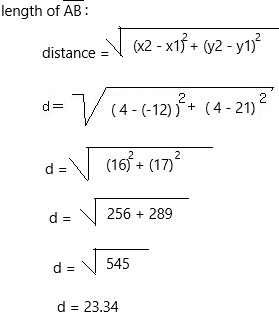
Therefore, the length of the line segment for the given endpoints is 23.34 units.
Question 5.
(-6, 9), (-6, 13)
Answer:
On a graph, the length of a line segment can be found by using the distance formula, between its endpoints. Else, we can use a ruler to measure the length of smaller line segments too.
The above-given coordinates:
(-6, 9) and (-6, 13)
A = (x1, y1) = (-6, -6)
B = (x2, y2) = (9, 13)
We can start with the distance formula:
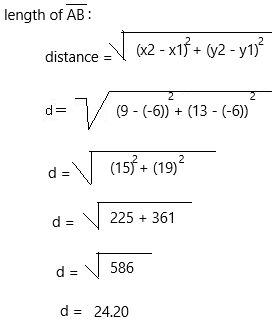
Therefore, the length of the line segment for the given endpoints is 24.20 units.
Question 6.
(17.1, 3), (21.4, 3)
Answer:
On a graph, the length of a line segment can be found by using the distance formula, between its endpoints. Else, we can use a ruler to measure the length of smaller line segments too.
The above-given coordinates:
(17.1, 3) and (21.4, 3)
A = (x1, y1) = (17.1, 21.4)
B = (x2, y2) = (3, 3)
We can start with the distance formula:
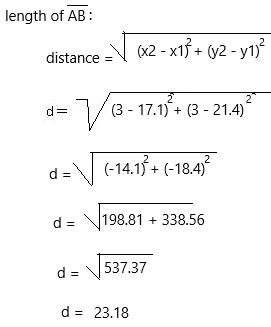
Therefore, the length of the line segment for the given endpoints is 23.18 units.
Question 7.
(-3, -12.5), (-3, 16.5)
Answer:
On a graph, the length of a line segment can be found by using the distance formula, between its endpoints. Else, we can use a ruler to measure the length of smaller line segments too.
The above-given coordinates:
(-3,-12.5) and (-3, 16.5)
A = (x1, y1) = (-3, -3)
B = (x2, y2) = (12.5, 16.5)
We can start with the distance formula:
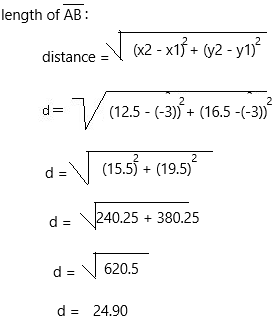
Therefore, the length of the line segment for the given endpoints is 24.90 units.
Test Prep
Question 8.
Find the area of the shaded region in square units.
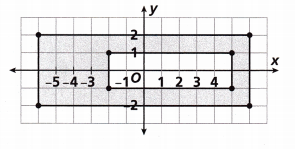
Answer:
We can name the rectangles in the above-given coordinate plane.
The outside rectangle is the ABCD
The inside rectangle is the PQRS
Area of the rectangle = length x width
area of the rectangle (ABCD):
length = 12; width = 4
area of rectangle (ABCD) = 12 x 4 = 48 units
Now find out the area of the rectangle (PQRS)
length = 7; width = 2
area of the rectangle (PQRS) = 7 x 2= 14 units
We know that the area of the rectangle ABCD and the area of the rectangle PQRS
Subtract both the area to get the shaded region.
Shaded region = area of the rectangle ABCD – an area of the rectangle PQRS
Shaded region = 48 – 14
Shaded region= 34 square units.
Question 9.
Rectangle ABCD has a perimeter of 22 units. The coordinates of the rectangle’s vertices are A(-4, 5), B(3, 5), C(3, x), and D(-4, x). Which could be the value of x?
(A) 7
(B) 4
(C) 1
(D) -9
Answer: Option C is correct.
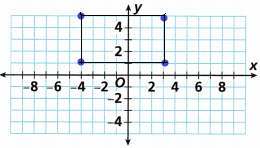
Perimeter = 22
We can do option verification.
If we count the squares between the points then we get length and width values.
By using the length and width we can get perimeter.
perimeter = 2(a+b)
length = 7; width = 4
Now substitute the values.
perimeter = 2(7 + 4)
perimeter = 2(11)
perimeter = 22.
we got the perimeter which is given in the above question when we substitute the x value as 1.
So, option C is correct.
Therefore, the coordinates of rectangle are:
A(-4, 5), B(3, 5), C(3, 1), and D(-4, 1)
Question 10.
Line segment DE is drawn on the coordinate plane. Which ordered pair could be the vertex of a rectangle with Segment DE as one side and an area of 28 square units? Select all that apply.
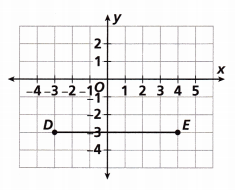
(A) (0, 1)
(B) (2, 0)
(C) (-3, 1)
(D) (-2, -2)
(E) (4, 4)
(F) (4, 1)
Answer: Options C and F are correct.
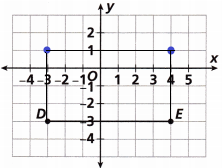
The vertex (4, 1) and (-3, 1) forms a rectangle.
Spiral Review
Question 11.
A triangle has vertices at A(-2, -1), B(-2, 4), and C(7, -1). In what quadrant is Vertex A located?
Answer:
The above-given vertices are: A(-2, -1), B(-2, 4), and C(7, -1)
The coordinates of vertex A(-2, -1)
Both signs are negative. So vertex A is located in the third quadrant.
– The lower left-hand corner of the graph is the third quadrant. It contains the negative values of both x and y.
Question 12.
A dozen doughnuts cost $2.99. To the nearest cent, what is the cost of 1 doughnut?
Answer:
We all know that dozen means a set of twelve.
12 doughnuts cost $2.99
The cost of each (1) doughnut = D
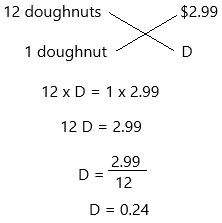
Therefore, each doughnut cost is $0.24
Question 13.
Mr Lee had $67. He bought a concert ticket and now has $11. Write an equation that can be used to find the price c of the concert ticket.
Answer:
The amount Mr Lee has is $67
After the concert ticket was bought he has $11.
The equation for the price of concert tickets is c.
C = $67 – $11
Question 14.
List three possible solutions for the inequality h < 34.
Answer:
In Algebra, inequality is a Mathematical statement that shows the relation between two expressions using the inequality symbol. The expressions on both sides of an inequality sign are not equal. It means that the expression on the left-hand side should be greater than or less than the expression on the right-hand side or vice versa. If the relationship between two algebraic expressions is defined using the inequality symbols, then it is called literal inequalities.
The solution is h < 34
but if we want to represent the solution in interval notation, then the equation will be:
