We included HMH Into Math Grade 6 Answer Key PDF Module 11 Review to make students experts in learning maths.
HMH Into Math Grade 6 Module 11 Review Answer Key
Vocabulary
Choose the correct term from the Vocabulary box to complete each statement.
Vocabulary
coordinate plane
axes
x-axis
y-axis
origin
quadrant
coordinates
polygon
vertex
reflection
Question 1.
A(n) ____________ is a closed plane figure formed by three or more line segments that intersect only at their endpoints.
Answer: polygon
Definition:
a polygon is a closed two-dimensional shape having straight line segments. It is not a three-dimensional shape. A polygon does not have any curved surface. A polygon should have at least three sides. Each side of the line segment must intersect with another line segment only at its endpoint.
Examples: Triangle, quadrilateral, pentagon, hexagon, heptagon, octagon, nonagon, decagon.
Question 2.
An ordered pair describes a point on a ____________ . The first number in an ordered pair describes the distance from the origin along the _________. The second number in an ordered pair describes the distance from the origin along the ___________.
Answer: coordinate plane, x-axis, y-axis
Ordered pairs are usually used in coordinate geometry to represent a point on a coordinate plane. Also, they are used to represent elements of a relation.
– An ordered pair is a pair formed by two elements that are separated by a comma and written inside the parentheses. For example, (x, y) represents an ordered pair, where ‘x’ is called the first element and ‘y’ is called the second element of the ordered pair.
Question 3.
The numbers of an ordered pair that locate a point on a coordinate plane are called _________.
Answer: axes
Suppose three planes intersect at a point O such that these three planes are mutually perpendicular to each other.
Question 4.
The point (0, 0) on the coordinate plane is called the ___________.
Answer: origin
the origin is the intersection of the x-axis and the y-axis. The position of a point in the coordinate plane is written as an ordered pair, (x, y), which tells us the position of the point relative to the origin.
Question 5.
A(n) ____________ of a figure is a transformation that flips the figure across a line.
Answer: reflection.
Rules:
– x-axis reflection. A reflection across the x-axis changes the position of the y-coordinate of all the points in a figure such that (x, y) becomes (x, -y).
– y-axis reflection. A reflection across the y-axis changes the position of the x-coordinate of all the points in a figure such that (x, y) becomes (-x, y).
Question 6.
The point on a polygon where two sides intersect is called a __________.
Answer: vertex
a vertex is a point where two or more curves, lines, or edges meet. As a consequence of this definition, the point where two lines meet to form an angle and the corners of polygons and polyhedra are vertices.
Question 7.
The point (1, 1) is located in ___________ I of the coordinate plane.
Answer: quadrant
The axes (x-axis and y-axis) of a two-dimensional Cartesian plane system divide the plane into four infinite regions called quadrants. The horizontal line or x-axis and vertical line or y-axis intersect each other at the right angle.
1st Quadrant: The upper right-hand corner of the graph is the first quadrant. In this quadrant the values of x and y both are positive.
Concepts and Skills
Use the coordinate plane to answer Problems 8-12.
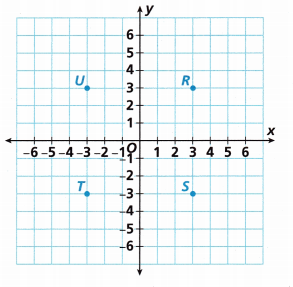
Question 8.
What type of figure has vertices at R, S, T, and U?
Answer:
– After connecting the coordinate points in a coordinate plane. Then we got square.
– count the squares.
– When we count we got all sides are equal.
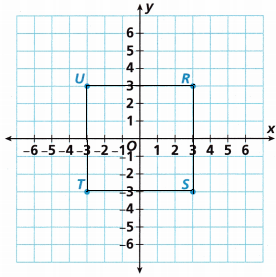
Question 9.
What is the area of Figure RSTU?
Answer:
We know that,
area of the square = side x side
– When we count the squares we got the side is 6.
Now substitute the side value in the above formula.
area of the square = 6 x 6
area of the square = 36 square units.
Therefore, the area of the figure RSTU is 36 square units.
Question 10.
What is the perimeter of Figure RSTU?
Answer:
The perimeter of a square is the distance covered by its four sides. Perimeter surrounds or outlines the shape in a two-dimensional plane.
– The formula to find the perimeter of a square is given below:
The perimeter of Square (P) = 4 × Side
We know that the side of a square is 6 units
Now substitute the value.
The perimeter of the square = 4 x 6
The perimeter of the square = 24 units.
Therefore, the perimeter of the figure RSTU is 24 units.
Question 11.
Graph the following points: M(0, -1), N(3\(\frac{1}{2}\), 0), P(-4, 0).
Answer:
– The above-given points M(0, -1), N(3\(\frac{1}{2}\), 0), P(-4, 0).
N(3 1/2, 0) = (7/2, 0) = (3.5, 0)
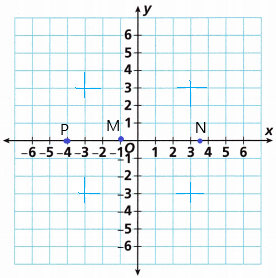
Question 12.
Use Tools What is the distance between Points C(4, 6) and D(-5, 6)? State what strategy and tool you will use to answer the question, explain your choice, and then find the answer.
Answer:
A distance on the coordinate plane can be found if we know the coordinates of the starting and ending points of that distance. Therefore, we can use the following steps to find distances on the coordinate plane:
Step 1: Determine the coordinates of the two given points on the plane. For example, we can have the points
A = (x1, y1) and B = (x2, y2).
Step 2: Apply the distance formula to find the distance between the given points.
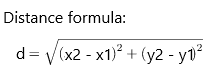
C = (x1, y1) = (4, -5)
D = (x2, y2) = (6, 6)
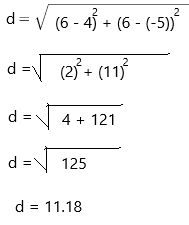
Use the coordinate plane to answer Problems 13-16.
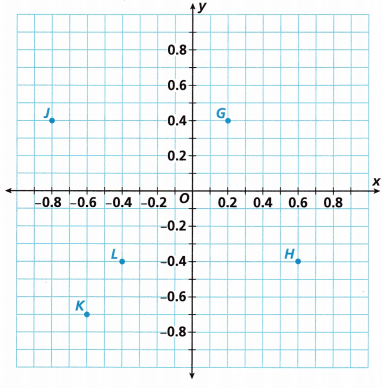
Question 13.
Write the ordered pair for each of the points on the graph.
Point G: _____________
Point H: _____________
Point L: _____________
Point J: _____________
Answer:
Ordered Pair = (x, y)
where, x = abscissa, the distance measure of a point from the x-axis.
and, y = ordinate, the distance measure of a point from the y-axis.
To graph a point, we have to draw a dot at the coordinates that correspond to the ordered pair. The x-coordinate tells us how many steps we have to take to on the x-axis. The y-coordinate tells us to have many steps to move on the y-axis.
The point G represents G(0.2, 0.4)
The point H represents H(0.6, -0.4)
The point L represents L(-0.4, -0.4)
The point J represents J(-0.8, 0.4)
Question 14.
Point K is reflected across the x-axis. What are the coordinates of its image after the reflection?
Answer:
– x-axis reflection. A reflection across the x-axis changes the position of the y-coordinate of all the points in a figure such that (x, y) becomes (x, -y).
– y-axis reflection. A reflection across the y-axis changes the position of the x-coordinate of all the points in a figure such that (x, y) becomes (-x, y).
Point K(-0.6, -0.7)
Now according to the above rule for the reflection over the x-axis then the point will be:
The reflection point K(-0.6, 0.7)
Question 15.
What is the distance from J to G?
![]() grid units, which equals
grid units, which equals ![]()
Answer:
The point J represents J(-0.8, 0.4)
The point G represents G(0.2, 0.4)
The quadrants are different with the same y-coordinate axes. So that we can use the absolute value.
|-0.8| – |0.2| = |-1| = 1
1.0 grid unis which equal to 1
Question 16.
What is the distance from L to H?
![]() grid units, which equals
grid units, which equals ![]()
Answer:
The point H represents H(0.6, -0.4)
The point L represents L(-0.4, -0.4)
The quadrants are different with the same y-coordinate axes. So that we can use the absolute value.
|-0.4| – |0.6| = |-1| = 1
1.0 grid unis which equal to 1
Question 17.
Find the distance between Points V(12, 14) and W(12, -16) without using a coordinate plane.
Answer:
A distance on the coordinate plane can be found if we know the coordinates of the starting and ending points of that distance. Therefore, we can use the following steps to find distances on the coordinate plane:
Step 1: Determine the coordinates of the two given points on the plane. For example, we can have the points
A = (x1, y1) and B = (x2, y2).
Step 2: Apply the distance formula to find the distance between the given points.
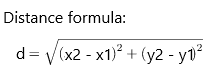
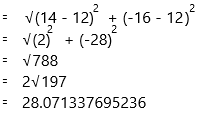
Question 18.
The vertices of Rectangle DEFG have these coordinates: D(4, 6), E(4, 1), F(0, 1), and G(0, 6). What is the area of Rectangle DEFG in square units?
Answer:
The above-given vertices: D(4, 6), E(4, 1), F(0, 1), and G(0, 6)
To find the area of the rectangle, first, we need to find out the length and width of the rectangle.
The length of the rectangle DE
D(4, 6), E(4, 1)
The quadrants are different with the same x-axis.
|6 – 1| = |5| = 5 units.
Therefore, the length of the rectangle is 5 units.
The width of the rectangle EF
E(4, 1), F(0, 1)
The quadrants are different with the same y-coordinates.
|4 – 1| = |3| = 3 units.
Therefore, the width of the rectangle is 3 units.
Now we can find out the area of the rectangle.
area = length x width
area = 5 x 3
area= 15 square units
Question 19.
The vertices of Rectangle RSTU have these coordinates: R(-8, 2), S(-8, -4), T(-2, -4), and U(-2, 2). What is the area of Rectangle RSTU in square units?
Answer:
The above-given vertices: R(-8, 2), S(-8, -4), T(-2, -4), and U(-2, 2)
To find the area of the rectangle, first, we need to find out the length and width of the rectangle.
The length of the rectangle ST
S(-8, -4), T(-2, -4)
The quadrants are different with the same x-axis.
|-8 – (-)2| = |6| = 6 units.
Therefore, the length of the rectangle is 6 units.
The width of the rectangle RS
R(-8, 2), S(-8, -4)
The quadrants are different with the same y-coordinates.
|2 – (-4)| = |6| = 6 units.
Therefore, the width of the rectangle is 6 units.
Now we can find out the area of the rectangle.
area = length x width
area = 6 x 6
area= 36 square units
Question 20.
The points M(-3, 2), N(-3, -4), P(2, -4) and Q(2, 2) form a rectangle.
A. What is the rectangle’s perimeter?
Answer:
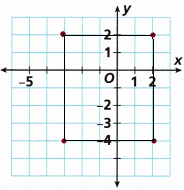
We count the squares between the points.
The length of the rectangle = 6 units
The width of the rectangle = 5 units
Since the perimeter is equal to the sum of all the polygon sides. Hence, in the case of a rectangle, the perimeter (P) is;
P = sum of all its four sides
P = a + b + a + b (Opposite sides of rectangle are equal)
P = 2 ( a+b)
Now add all the lengths and widths.
Perimeter = 2(6 + 5)
Perimeter = 2 (11)
Perimeter = 22 units
Therefore, the perimeter of the rectangle MNPQ is 22 units
B. What is the rectangle’s area in square units?
Answer:
The length of the rectangle = 6
The width of a rectangle = 5
Area of the rectangle = length x width
A = 6 x 5
A = 30 square units.
Question 21.
Which point is a reflection of (-5, 1.8) across the y-axis on a coordinate plane?
(A) (5, 1.8)
(B) (-5, -1.8)
(C) (-5, 1.8)
(D) (5, -1.8)
Answer: Option A is correct.

– x-axis reflection. A reflection across the x-axis changes the position of the y-coordinate of all the points in a figure such that (x, y) becomes (x, -y).
– y-axis reflection. A reflection across the y-axis changes the position of the x-coordinate of all the points in a figure such that (x, y) becomes (-x, y).
Given point: (-5, 1.8)
Now according to the above rule for the reflection over the y-axis then the point will be:
The reflection point (5, 1.8)