We included HMH Into Math Grade 6 Answer Key PDF Module 3 Lesson 3 Explore Division of Mixed Numbers to make students experts in learning maths.
HMH Into Math Grade 6 Module 3 Lesson 3 Answer Key Explore Division of Mixed Numbers
I Can find the quotient of a mixed number or fraction and a mixed number, fraction, or whole number.
Spark Your Learning
Four friends go hiking. They bring snacks, a compass, and 3\(\frac{1}{3}\) quarts of water. If they share the water equally, how many quarts will each person get?


Answer:
Each person will get \(\frac{5}{6}\) quarts,
Explanation:
Given Four friends go hiking. They bring snacks,
a compass, and 3\(\frac{1}{3}\) quarts of water.
If they share the water equally, Number of quarts will
each person get is 3\(\frac{1}{3}\) ÷ 4 =
\(\frac{3 X 3 + 1}{3}\) X \(\frac{1}{4}\) =
\(\frac{10}{3}\) X \(\frac{1}{4}\) =
\(\frac{10 x 1}{3 X 4}\) = \(\frac{10}{12}\)
as both goes in 2 we will get \(\frac{5}{6}\).
Turn and Talk How could you use a model to solve this problem? Explain.
Answer:
Explanation:
Given 3\(\frac{1}{3}\) ÷ 4 we use area model
as shown above first we divide 3 fulls and \(\frac{1}{3}\)
by dividing by 3 vertical lines then we divide by 4 using
horizontal lines we get filled part \(\frac{10}{12}\) with
green color as shown above.
Build Understanding
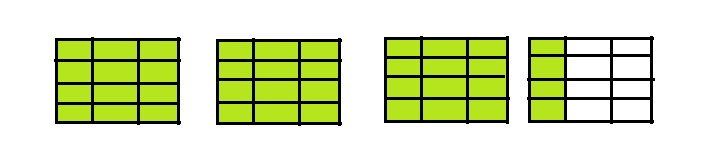
1. Three friends go on a hike that is 4\(\frac{1}{2}\) miles long. If they take breaks as shown at the right, then how many breaks will they take?

A. Draw a bar model to represent the mixed number 4\(\frac{1}{2}\). How many equal-sized rectangles did you need? How many of them did you shade?

B. How can you find how many times the hikers must take a break?
____________________________
C. Use your bar model to find how many breaks the three friends will take. How did you do it?

D. How many groups of \(\frac{3}{4}\) are in 4\(\frac{1}{2}\)? Use your model to count.
E. Write an expression to show what operation you would use to represent this situation.
____________________________
A. 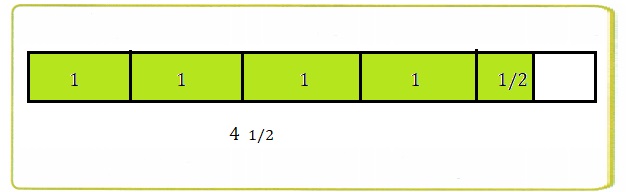
B. Dividing by \(\frac{3}{4}\),
C.
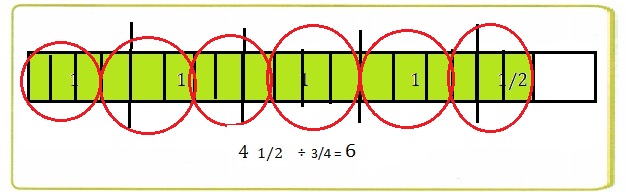
D. 6 groups,
E. Expression:
g = 4\(\frac{1}{2}\) ÷ \(\frac{3}{4}\),
Explanation:
Given three friends go on a hike that is 4\(\frac{1}{2}\) miles
long. If they take breaks as shown at the right,
A. Drawn a bar model to represent the mixed number
4\(\frac{1}{2}\). Number of equal-sized
rectangles I need are 5, Four and half of them are shaded.
B. Given taking break every \(\frac{3}{4}\) mile
So number of times the hikers must take a break is
Dividing by \(\frac{3}{4}\).
C. Used my bar model to find how many breaks
the three friends will take. Breaking 4\(\frac{1}{2}\) into
\(\frac{3}{4}\).
D. Number of groups of \(\frac{3}{4}\) are in
4\(\frac{1}{2}\) used my model to count are 6
groups circled with red as shown above.
E. Expression to show what operation I would use to
represent this situation is let g be number of groups of
\(\frac{3}{4}\) are in 4\(\frac{1}{2}\) are
g = 4\(\frac{1}{2}\) ÷ \(\frac{3}{4}\).
Turn and Talk How could you use another method to solve this problem?
Answer:
Directly by solving,
They take 6 breaks,
Explanation:
Given three friends go on a hike that is 4\(\frac{1}{2}\) miles long.
If they take breaks as shown at the right as \(\frac{3}{4}\) then
Number of breaks will they take are
4\(\frac{1}{2}\) ÷ \(\frac{3}{4}\)=
\(\frac{4 x 2 + 1}{2}\) X \(\frac{4}{3}\) =
\(\frac{9}{2}\) X \(\frac{4}{3}\) =
\(\frac{9 X 4}{2 X 3}\) = 3 X 2 = 6.
Step It Out
2. Jamarion has 4\(\frac{2}{5}\) pounds of peanuts that he needs to divide evenly into 6 bins. How many pounds of peanuts will be in each bin?
A. What expression could you use to solve the problem?
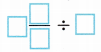
B. Will the quotient be greater than or less than 1? How do you know?
___________________________
C. Write the mixed number as a fraction greater than 1.
![]()
D. Complete the steps to divide 4 by 6.
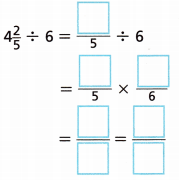

E. Complete the sentences to describe how to solve the division problem.
Write the _______ as a fraction greater than 1.
Change the operation to ____ and replace the ____ with its reciprocal.
Multiply. There will be ____ pound of peanuts in each bin.
Answer:
A.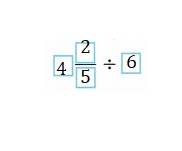
B. Less than 1, by seeing denominator,
C.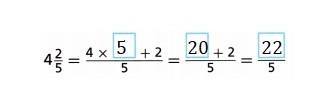
D. 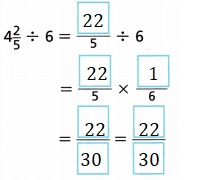
E. Write the mixed number as a fraction greater than 1.
Change the operation to multiplication and replace
the value with its reciprocal. Multiply.
There will be \(\frac{22}{30}\) pound of peanuts in each bin.
Explanation:
Given Jamarion has 4\(\frac{2}{5}\) pounds of
peanuts that he needs to divide evenly into 6 bins.
A. Wrote the expression could I use to solve the problem
4\(\frac{2}{5}\) ÷ 6,
B. Less than 1 as denominator is more than the numerator,
C. Wrote the mixed number as a fraction greater than 1 as
\(\frac{22}{5}\),
D. Completed the steps to divide 4 by 6 as
\(\frac{22}{5}\) ÷ 6 =
\(\frac{22}{5}\) X \(\frac{1}{6}\) =
\(\frac{22 X 1}{5 X 6}\) = \(\frac{22}{30}\),
E. Completed the sentences to describe
how to solve the division problem as
Write the mixed number as a fraction greater than 1.
Change the operation to multiplication and replace
the value with its reciprocal. Multiply.
There will be \(\frac{22}{30}\) pound of peanuts in each bin.
3. Consider the division problem 2\(\frac{1}{4}\) ÷ \(\frac{3}{8}\). Complete the steps to show how to divide the mixed number by the fraction.
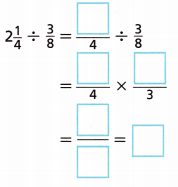
Answer:
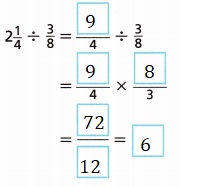
Explanation:
Completed the steps to show how to divide the
mixed number by the fraction 2\(\frac{1}{4}\) ÷ \(\frac{3}{8}\) =
\(\frac{9}{4}\) X \(\frac{8}{3}\) =
\(\frac{9 X 8}{4 X 3}\) = \(\frac{72}{12}\)
both goes in 12, so \(\frac{6 X 12}{12}\) = 6.
Turn and Talk When will the quotient be greater than the dividend in a division problem?
Answer:
Dividing a number which is greater than zero
by a number between 0 and 1,
Negative dividend divided by positive divisor,
Explanation:
When dividing a number which is greater than zero
by a number between 0 and 1,
then the quotient is greater than the dividend.
If the dividend is negative, For example:
or
4. Phil works at a pet store where fish are sold. He has 5\(\frac{1}{4}\) liters of water to add to several aquariums, if each aquarium needs \(\frac{7}{8}\) liter of water, how many aquariums can he fill?

A. What expression do you need to use to solve the problem?
_____________________
B. Will the quotient be greater than or less than 1? How do you know?
C. Complete the steps to show how to divide the mixed number by the fraction. Then complete the solution.
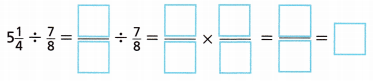
Phil can fill ____ aquariums with 5 liters of water.
D. In Part C, you multiplied the fractions and then divided to get the answer. However, you can simplify the solution before you multiply. Complete the steps to see how to do this.
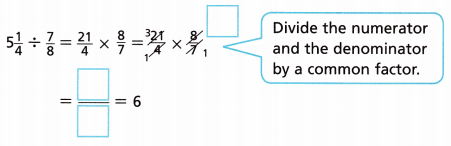
Answer:
A. 5\(\frac{1}{4}\) B. Quotient is greater than 1,
c. 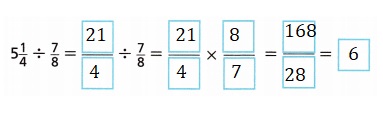
Phil can fill 6 aquariums with 5liters of water,
D. 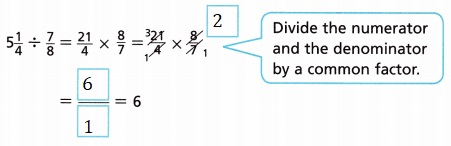
Explanation:
Given Phil works at a pet store where fish are sold.
He has 5\(\frac{1}{4}\) liters of water to
add to several aquariums, if each aquarium needs
\(\frac{7}{8}\) liter of water
A. Expression I need to use to solve the problem is
5\(\frac{1}{4}\) less than 5\(\frac{1}{4}\) so quotient will be greater
than 1.
C. Completed the steps to show how to divide
the mixed number by the fraction. Then completed the solution.
Phil can fill 6 aquariums with 5liters of water.
D. In Part C, I have multiplied the fractions and
then divided to get the answer. However, I can simplify
the solution before I multiply. Completed the steps to
see how to do this above.
Check Understanding
Question 1.
Dion has a pitcher of lemonade holding 3\(\frac{1}{2}\) pints, and he wants to make
\(\frac{1}{2}\)-pint servings.
A. How many groups of \(\frac{1}{2}\) are in 3\(\frac{1}{2}\)? ____________
B. Write an expression to show what operation you would use to represent this situation.
_____________________
Answer:
A. 7 groups,
B. 3\(\frac{1}{2}\)
Explanation:
Given Dion has a pitcher of lemonade holding
3\(\frac{1}{2}\) pints and he wants to
make \(\frac{1}{2}\)-pint servings,
A. Number of groups of \(\frac{1}{2}\)
are in 3\(\frac{1}{2}\)–
3\(\frac{1}{2}\)
Question 2.
Jessica runs 2\(\frac{1}{2}\) miles in 16\(\frac{1}{4}\) minutes. What is Jessica’s average time per mile in minutes?
_____________________
Answer:
Explanation:
Jessica runs 2\(\frac{1}{2}\) miles in
16\(\frac{1}{4}\) minutes.
Jessica’s average time per mile in minutes is
16\(\frac{1}{4}\) denominator we can write in mixed fraction as
On Your Own
Question 3.
Javier exercises for 2\(\frac{1}{2}\) hours every Saturday. His exercise weightlifting includes two parts. If he spends the same amount of time on both parts, how many hours does he spend weightlifting?

Answer:
Explanation:
Given Javier exercises for 2\(\frac{1}{2}\) hours every Saturday.
His exercise weightlifting includes two parts.
If he spends the same amount of time on both parts,
Number of hours does he spend weightlifting are
2\(\frac{1}{2}\) denominator we can write in
mixed fraction as
Question 4.
Reason A baker would like to store 12\(\frac{3}{4}\) pounds of flour in containers that each hold 3\(\frac{1}{2}\) pounds of flour. How many containers will the baker need? Explain.
Answer:
3
Explanation:
Given a baker would like to store 12\(\frac{3}{4}\) pounds
of flour in containers that each hold 3\(\frac{1}{2}\) pounds
of flour. Number of containers will the baker need are
12\(\frac{3}{4}\) denominator we can write in
mixed fraction as 3
Question 5.
A rectangular garden has an area of 46\(\frac{1}{2}\) square feet. If the garden is 7\(\frac{1}{2}\) feet long, how many feet wide is it?
_____________________
Answer:
Width is 6
Explanation:
Given a rectangular garden has an area of
46\(\frac{1}{2}\) square feet. If the garden is
7\(\frac{1}{2}\) feet long, So width is
46\(\frac{1}{2}\) denominator we can write in
mixed fraction as 6
Question 6.
Kim is building a fence that is 32\(\frac{1}{2}\) feet long. She has already put the first post in place. There will be additional posts every 2\(\frac{1}{2}\) feet. How many additional posts will Kim need?
Answer:
Kim need 13 posts,
Explanation:
Given Kim is building a fence that is 32\(\frac{1}{2}\) feet long.
She has already put the first post in place. There will be additional posts every 2\(\frac{1}{2}\) feet. Number of additional posts will Kim need are
32\(\frac{1}{2}\)
Question 7.
Dana has a piece of lumber that is 22\(\frac{3}{4}\) feet long. She needs pieces that are 3\(\frac{1}{4}\) feet long. How many pieces can she cut from the 22\(\frac{3}{4}\)-foot piece of lumber?
_____________________
Answer:
7 pieces,
Explanation:
Given Dana has a piece of lumber that is
22\(\frac{3}{4}\) feet long. She needs pieces that
are 3\(\frac{1}{4}\) feet long. Number of pieces can
she cut from the 22\(\frac{3}{4}\)-foot piece of lumber is
22\(\frac{3}{4}\)
For Problems 8-11, divide.
Question 8.
2\(\frac{5}{6}\) ÷ \(\frac{1}{2}\) ____________
Answer:
5
Explanation:
Given 2\(\frac{5}{6}\) denominator we can write in mixed fraction as 5
Question 9.
5\(\frac{1}{5}\) ÷ 3 ____________
Answer:
1
Explanation:
Given 5\(\frac{1}{5}\) denominator we can write in
mixed fraction as 1
Question 10.
1\(\frac{1}{5}\) ÷ 2\(\frac{3}{10}\) ____________
Answer:
Explanation:
Given 1\(\frac{1}{5}\)
Question 11.
\(\frac{3}{4}\) ÷ 2\(\frac{3}{8}\) ____________
Answer:
Explanation:
Given \(\frac{3}{4}\)
Question 12.
At a zoo, a tiger eats 8\(\frac{3}{4}\) pounds of a specially-prepared ground beef every day. If the zookeeper buys 87\(\frac{1}{2}\) pounds of the ground beef, how many days will it last?

Answer:
10 days,
Explanation:
Given at a zoo, a tiger eats 8\(\frac{3}{4}\) pounds of
a specially-prepared ground beef every day.
If the zookeeper buys 87\(\frac{1}{2}\) pounds of
the ground beef, Number of days will it last is
87\(\frac{1}{2}\)
Question 13.
At her bakery, Sherry has 6\(\frac{1}{2}\) pounds of cherries to make tarts. If she uses \(\frac{1}{4}\) pound of cherries for each tart, how many tarts can she make?
Answer:
26 tarts,
Explanation:
Given at Sherry bakery she has has 6\(\frac{1}{2}\) pounds of
cherries to make tarts. If she uses \(\frac{1}{4}\) pound of
cherries for each tart, number of tarts can she make are
6\(\frac{1}{2}\)
Question 14.
Critique Reasoning Dan says that 24\(\frac{1}{2}\) ÷ 12\(\frac{1}{2}\) = 2, because 24 ÷ 12 = 2. Sam disagrees and thinks there will be fewer than 2 groups of 12\(\frac{1}{2}\) in 24\(\frac{1}{2}\). Who is correct and why? What is 24\(\frac{1}{2}\) ÷ 12\(\frac{1}{2}\)?
Answer:
Sam is correct as 24\(\frac{1}{2}\) ÷ 12\(\frac{1}{2}\) =
not 24 ÷ 12 = 2,
Explanation:
Given Dan says that 24\(\frac{1}{2}\) ÷
12\(\frac{1}{2}\) = 2, because 24 ÷ 12 = 2.
Sam disagrees and thinks there will be fewer than 2
groups of 12\(\frac{1}{2}\) in 24\(\frac{1}{2}\).
Checking 24\(\frac{1}{2}\) ÷ 12\(\frac{1}{2}\) =
Question 15.
Reason Mason is laying tiles on an entryway.The tiles are each \(\frac{2}{9}\) foot long, and the entryway is 7\(\frac{1}{2}\) feet long. How many tiles will Mason need to cover the length of the entryway? Explain.
Answer:
Number of tiles will Mason need to cover the length of the entryway are
Explanation:
Given Mason is laying tiles on an entryway.
The tiles are each \(\frac{2}{9}\) foot long and the
entryway is 7\(\frac{1}{2}\) feet long.
Number of tiles will Mason need to cover the length of the entryway are
7\(\frac{1}{2}\) ÷ \(\frac{2}{9}\) =
For Problems 16—19, write the equivalent multiplication expression.
Question 16.
2\(\frac{1}{6}\) ÷ \(\frac{3}{4}\) ____________
Answer:
Explanation:
Given 2\(\frac{1}{6}\) denominator we can write in
mixed fraction as 2
Question 17.
4\(\frac{5}{8}\) ÷ 2\(\frac{1}{2}\) ____________
Answer:
Explanation:
Given 4\(\frac{5}{8}\) ÷ 2\(\frac{1}{2}\) =
Question 18.
3\(\frac{1}{3}\) ÷ \(\frac{9}{10}\) ____________
Answer:
Explanation:
Given 3\(\frac{1}{3}\) denominator we can write in
mixed fraction as 3
Question 19.
5\(\frac{2}{5}\) ÷ 1\(\frac{7}{8}\) ____________
Answer:
Explanation:
Given 5\(\frac{2}{5}\) ÷ 1\(\frac{7}{8}\) =
I’m in a Learning Mindset!
What can I apply from my previous work with LCMs and GCFs to better understand division with mixed numbers?
______________________
Answer:
GCF’s,
Explanation:
A mixed number is a number expressed as the sum of a
whole number and a frraction, When we divide a number
by a mixed number, first rewrite the mixed number as an
improper fractions . Then multiply the number by the
reciprocal of the improper fraction then simplify using GCF’s.
Lesson 3.3 More Practice/Homework
Explore Division of Mixed Numbers
Question 1.
Darlene cuts a 9\(\frac{1}{2}\)-foot-long pipe into pieces that are 2\(\frac{3}{8}\) feet long. How many pieces of pipe does she have? Explain.

Answer:
4 pieces of pipe,
Explanation:
Given Darlene cuts a 9\(\frac{1}{2}\)-foot-long
pipe into pieces that are 2\(\frac{3}{8}\) feet long.
Number of pieces of pipe does she have are
9\(\frac{1}{2}\) ÷ 2\(\frac{3}{8}\) =
Question 2.
Attend to Precision Jonathan will run a 6\(\frac{1}{4}\)-mile relay with 4 other team members, where each team member runs an equal distance. How many miles will Jonathan run?
Answer:
1\(\frac{1}{4}\),
Explanation:
Given Jonathan will run a 6\(\frac{1}{4}\)-mile relay
with 4 other team members, where each team member runs
an equal distance. So number of many miles will Jonathan run
are 6\(\frac{1}{4}\)
Question 3.
Every 14 days, Debbie’s dog eats 4\(\frac{1}{5}\) pounds of dog food. If Debbie’s dog eats the same amount of food each day, how many pounds does her dog eat per day?
Answer:
Explanation:
Given every 14 days, Debbie’s dog eats 4\(\frac{1}{5}\) pounds of
dog food. If Debbie’s dog eats the same amount of food each day,
Number of pounds does her dog eat per day is
4\(\frac{1}{5}\)
Question 4.
Math on the Spot One serving of Roberto’s favorite yogurt is 6\(\frac{1}{2}\) ounces. How many servings are in a 16\(\frac{1}{4}\)-ounce container?
___________________________
___________________________
Answer:
Explanation:
Given one serving of Roberto’s favorite yogurt is
6\(\frac{1}{2}\) ounces. Number of servings
are in a 16\(\frac{1}{4}\)-ounce container are
16\(\frac{1}{4}\) ÷ 6\(\frac{1}{2}\) =
Question 5.
Brad reads his favorite book for 1\(\frac{1}{4}\) hours each day. If he has read the book for 22\(\frac{1}{2}\) hours so far, how many days has he read it? Show how you know.
Answer:
18 days,
Explanation:
Given Brad reads his favorite book for 1\(\frac{1}{4}\) hours
each day. If he has read the book for 22\(\frac{1}{2}\) hours
so far, number of days has he read it are
22\(\frac{1}{2}\) ÷ 1\(\frac{1}{4}\) =
For Problems 6-11, find the quotient.
Question 6.
\(\frac{3}{4}\) ÷ 1\(\frac{1}{10}\) ____________
Answer:
Explanation:
Given \(\frac{3}{4}\)
Question 7.
5\(\frac{1}{2}\) ÷ 6 ____________
Answer:
Explanation:
Given 5\(\frac{1}{2}\) Question 8.
1\(\frac{2}{15}\) ÷ \(\frac{1}{5}\) ____________
Answer:
Explanation:
Given 1\(\frac{2}{15}\) denominator we can write in
mixed fraction as 5
Question 9.
2\(\frac{1}{2}\) ÷ 2\(\frac{5}{8}\) ____________
Answer:
Explanation:
Given 2\(\frac{1}{2}\) ÷ 2\(\frac{5}{8}\) =
Question 10.
4\(\frac{2}{3}\) ÷ 2\(\frac{1}{3}\) ____________
Answer:
Explanation:
Given 4\(\frac{2}{3}\) ÷ 2\(\frac{1}{3}\) =
Question 11.
2\(\frac{1}{5}\) ÷ 3\(\frac{1}{7}\) ____________
Answer:
Explanation:
Given 2\(\frac{1}{5}\) ÷ 3\(\frac{1}{7}\) =
Test Prep
Question 12.
Harley rides her bicycle the same distance every day for 4 days. The total distance she rides is 8\(\frac{1}{4}\) miles. How many miles does she ride each day?
_____________________
Answer:
2\(\frac{1}{16}\) miles each day,
Explanation:
Given Harley rides her bicycle the same distance
every day for 4 days. The total distance she rides is
8\(\frac{1}{4}\) miles. Number of miles
does she ride each day is
8\(\frac{1}{4}\) ÷ 4 =
denominator we can write in
mixed fraction as 2
Question 13.
An equation is shown.
1\(\frac{2}{3}\) × ![]() = \(\frac{1}{4}\)
= \(\frac{1}{4}\)
What factor is missing from the equation?
A. \(\frac{3}{20}\)
B. \(\frac{5}{12}\)
C. 2\(\frac{2}{5}\)
D. 6\(\frac{2}{3}\)
Answer:
A. \(\frac{3}{20}\),
Explanation:
Given 1\(\frac{2}{3}\) × ![]() = \(\frac{1}{4}\),
= \(\frac{1}{4}\),
let x be the missing factor in the equation so
1\(\frac{2}{3}\) X x = \(\frac{1}{4}\),
x = \(\frac{1}{4}\) ÷ 1\(\frac{2}{3}\),
x = \(\frac{1}{4}\) ÷ \(\frac{1 X 3 + 2}{3}\),
x = \(\frac{1}{4}\) X \(\frac{3}{5}\),
x = \(\frac{1 X 3}{4 X 5}\) = \(\frac{3}{20}\)
matches with bit A.
Question 14.
An expression is shown.
1\(\frac{3}{7}\) ÷ 1\(\frac{1}{3}\)
What is the value of the expression as a mixed number? ____________
Answer:
1\(\frac{1}{14}\),
Explanation:
Given an expression is shown
1\(\frac{3}{7}\) ÷ 1\(\frac{1}{3}\)
the value of the expression as a mixed number is
1\(\frac{3}{7}\) ÷ 1\(\frac{1}{3}\),
\(\frac{1 X 7 + 3}{7}\) ÷ \(\frac{1 X 3 + 1}{3}\),
\(\frac{10}{7}\) X \(\frac{3}{4}\),
\(\frac{10 X 3}{7 X 4}\) = \(\frac{15}{14}\)
denominator we can write in
mixed fraction as 1
Question 15.
What multiplication expression would you use to find the quotient of 3\(\frac{1}{2}\) ÷ 2\(\frac{1}{5}\) ?
A. \(\frac{2}{7}\) × \(\frac{5}{11}\)
B. \(\frac{2}{7}\) × \(\frac{11}{5}\)
C. \(\frac{7}{2}\) × \(\frac{5}{11}\)
D. \(\frac{7}{2}\) × \(\frac{11}{5}\)
Answer:
C. \(\frac{7}{2}\) × \(\frac{5}{11}\),
Explanation:
Solving 3\(\frac{1}{2}\) ÷ 2\(\frac{1}{5}\) =
\(\frac{3 X 2 + 1}{2}\) ÷ \(\frac{2 X 5 + 1}{5}\),
\(\frac{7}{2}\) X \(\frac{5}{11}\),
So multiplication expression I would use to find the quotient is
bit C. \(\frac{7}{2}\) X \(\frac{5}{11}\).
Spiral Review
Question 16.
Which number is greater, -18 or -16?
_____________________
Answer:
– 16 is greater,
Explanation:
Given to find which number is grater -18 or -16,
Greater depends on whether we are greater
towards positive side or negative side, as it is negative side
so – 16 is greater.
Question 17.
An expression is shown.
\(\frac{4}{3}\) × \(\frac{4}{5}\)
What is the value of the expression? ___________
Answer:
1\(\frac{1}{15}\),
Explanation:
Given expression is \(\frac{4}{3}\) × \(\frac{4}{5}\),
The value of the expresion is
\(\frac{4}{3}\) X \(\frac{4}{5}\) =
\(\frac{4 X 4}{3 X 5}\) = \(\frac{16}{15}\)
denominator we can write in
mixed fraction as 1
Question 18.
An expression is shown.
\(\frac{4}{5}\) ÷ \(\frac{3}{5}\)
What is the value of the expression? ___________
Answer:
1\(\frac{1}{3}\),
Explanation:
Given expression is \(\frac{4}{5}\) ÷ \(\frac{3}{5}\),
The value of the expresion is
\(\frac{4}{5}\) ÷ \(\frac{3}{5}\) =
\(\frac{4}{5}\) X \(\frac{5}{3}\)
\(\frac{4 X 5}{5 X 3}\) = \(\frac{4}{3}\)
denominator we can write in
mixed fraction as 1