We included HMH Into Math Grade 5 Answer Key PDF Module 8 Lesson 6 Interpret Fraction Multiplication as Scaling to make students experts in learning maths.
HMH Into Math Grade 5 Module 8 Lesson 6 Answer Key Interpret Fraction Multiplication as Scaling
I Can explain how the size of the product compares to the size of one factor.
Spark Your Learning
The painting shown is resized to \(\frac{3}{4}\) of its original size. How does the height of the resized painting compare to the height of the original painting? Is the height of the resized painting more than or less than \(\frac{3}{4}\) foot?

Answer:
The height is less than \(\frac{3}{4}\) foot.
Explanation:
Given that the painting shown is resized to \(\frac{3}{4}\) of its original size. So the height is less than \(\frac{3}{4}\) foot.
Draw a visual model to represent your thinking. Justify your reasoning.

Answer:
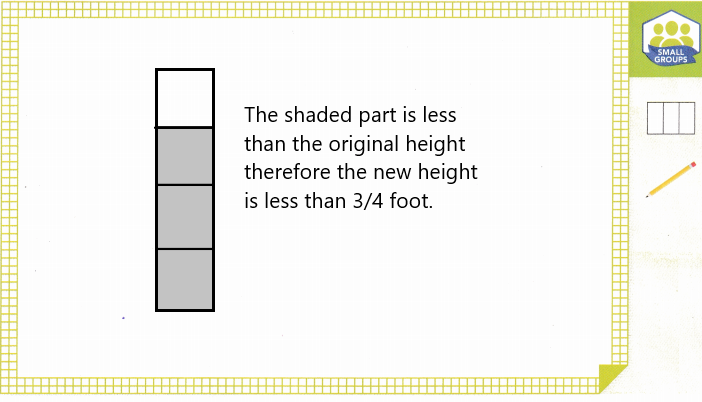
Turn and Talk How do you know when a product will be less than one of its factors?
Build Understanding
1. A roller hockey puck typically weighs \(\frac{1}{4}\) pound. An ice hockey puck typically weighs \(\frac{3}{2}\) times as much as a roller hockey puck.

Answer:
The expression will be \(\frac{3}{2}\) × \(\frac{1}{4}\) = \(\frac{3}{8}\) pounds.
Explanation:
Given that a roller hockey puck typically weighs \(\frac{1}{4}\) pound and an ice hockey puck typically weighs \(\frac{3}{2}\) times as much as a roller hockey puck. So the expression will be \(\frac{3}{2}\) × \(\frac{1}{4}\) which is \(\frac{3}{8}\) pounds.
A. Write a multiplication expression to model the problem. ____
Answer:
The expression is \(\frac{3}{2}\) × \(\frac{1}{4}\) = \(\frac{3}{8}\) pounds.
Explanation:
The multiplication expression is \(\frac{3}{2}\) × \(\frac{1}{4}\) which is \(\frac{3}{8}\) pounds.
B. How do your factors from Part A compare to 1? _____
Answer:
\(\frac{3}{2}\) > \(\frac{1}{4}\).
Explanation:
By comparing part A to 1 \(\frac{3}{2}\) is greater than \(\frac{1}{4}\).
C. What is the product of a number multiplied by 1? _____
Answer:
The product of a number multiplied by 1 we will get the same value.
D. Will the product of a number multiplied by a factor greater than 1 be less than or greater than that number? How do you know?
_____________________
_____________________
_____________________
Answer:
Here, the product of a number multiplied by a factor is greater than that number.
E. Predict whether the typical weight of an ice hockey puck is greater than, less than, or equal to the typical weight of a roller hockey puck. Explain your reasoning.
_____________________
_____________________
Answer:
Here, ice hockey puck weighs more than the roller hockey puck.
Turn and Talk By what fractions could you multiply \(\frac{1}{4}\) to get a product that is less than \(\frac{1}{4}\)? Equal to \(\frac{1}{4}\)? Explain.
Step It Out
2. A new skateboard ramp is designed that has a width that is \(\frac{2}{3}\) of the width of the ramp shown.

A. Is the width of the new ramp greater than or less than the width of the ramp shown? How do you know?
_____________________
_____________________
_____________________
Answer:
\(\frac{2}{3}\) is less than \(\frac{5}{6}\).
Explanation:
Given that a new skateboard ramp is designed that has a width that is \(\frac{2}{3}\). So \(\frac{2}{3}\) is less than \(\frac{5}{6}\).
B. By what factor could the new ramp be resized so that the width is greater than the width of the original ramp? Explain.
_____________________
Turn and Talk What would the scale factor have to be if you wanted the width of the ramp to stay the same? Explain.
Check Understanding Math Board
Question 1.
A vehicle traveling 70 miles each hour needs \(\frac{1}{10}\) mile to come to a complete stop. Engineers are designing a new vehicle that can come to a complete stop in \(\frac{1}{2}\) of that distance. How does the stopping distance of the new vehicle compare to the stopping distance of the original vehicle?
Answer:
The new vehicle is shorter.
Explanation:
Given that a vehicle traveling 70 miles each hour needs \(\frac{1}{10}\) mile to come to a complete stop and a engineers are designing a new vehicle that can come to a complete stop in \(\frac{1}{2}\) of that distance. So by comparing the new vehicle is shorter.
A \(\frac{3}{8}\)-yard-long toy bus is rescaled as modeled by the expressions shown in 2-4. Use shorter, longer, or same to describe how the length of the rescaled bus compares to the original length.
Question 2.
\(\frac{8}{1}\) × \(\frac{3}{8}\)
Answer:
\(\frac{8}{1}\) × \(\frac{3}{8}\) > 1.
Explanation:
Given the equation is \(\frac{8}{1}\) × \(\frac{3}{8}\) which is 3 greater than \(\frac{3}{8}\).
Question 3.
\(\frac{8}{8}\) × \(\frac{3}{8}\)
Answer:
\(\frac{8}{8}\) × \(\frac{3}{8}\) = \(\frac{3}{8}\).
Explanation:
Given the equation is \(\frac{8}{8}\) × \(\frac{3}{8}\) which is \(\frac{3}{8}\) same as \(\frac{3}{8}\).
Question 4.
\(\frac{1}{2}\) × \(\frac{3}{8}\)
Answer:
\(\frac{1}{2}\) × \(\frac{3}{8}\) < \(\frac{3}{8}\).
Explanation:
Given the equation is \(\frac{1}{2}\) × \(\frac{3}{8}\) which is \(\frac{3}{16}\) smaller than \(\frac{3}{8}\).
On Your Own
Question 5.
STEM Human and animal brains are made of millions of neurons. Dogs have about 530,000,000 brain neurons. Cats have about \(\frac{1}{2}\) of this amount of brain neurons. Which animal has more brain neurons? Explain.
Answer:
Dogs have more amount of brain neurons.
Explanation:
Given that dogs have about 530,000,000 brain neurons and cats have about \(\frac{1}{2}\) of this amount of brain neurons. So dogs have more amount of brain neurons.
For 6-8, complete the statement with equal to, greater than, or less than.
Question 6.
\(\frac{4}{5}\) × \(\frac{1}{3}\) will be ___ \(\frac{1}{3}\).
Answer:
\(\frac{4}{5}\) × \(\frac{1}{3}\) < \(\frac{1}{3}\).
Explanation:
Given that the equation is \(\frac{4}{5}\) × \(\frac{1}{3}\) which is less than \(\frac{1}{3}\).
Question 7.
1 × \(\frac{1}{4}\) will be ___ \(\frac{1}{4}\).
Answer:
1 × \(\frac{1}{4}\) = \(\frac{1}{4}\).
Explanation:
Given that the equation is 1 × \(\frac{1}{4}\) which is equal to \(\frac{1}{4}\).
Question 8.
6 × \(\frac{2}{5}\) will be ___ \(\frac{2}{5}\).
Answer:
6 × \(\frac{2}{5}\) > 2\(\frac{2}{5}\).
Explanation:
Given that the equation is 6 × \(\frac{2}{5}\) which is greater than \(\frac{12}{5}\) = 2\(\frac{2}{5}\).
Chicago’s Willis Tower measures 1,729 feet tall at its tip. The tower is rescaled as modeled by the expressions shown in 9-11. Use shorter, taller, or same to describe how the height of the rescaled tower compares to the original height.
Question 9.
\(\frac{9}{9}\) × 1,729
Answer:
1,729 = 1,729.
Explanation:
Given that the equation is \(\frac{9}{9}\) × 1,729 which is 1,729 same as tower measures.
Question 10.
\(\frac{2}{1}\) × 1,729
Answer:
3,458 > 1,729.
Explanation:
Given that the equation is \(\frac{2}{1}\) × 1,729 which is 3,458 greater than 1,729.
Question 11.
\(\frac{1}{9}\) × 1,729
Answer:
192\(\frac{1}{9}\) < 1,729.
Explanation:
Given that the equation is \(\frac{1}{9}\) × 1,729 which is 192\(\frac{1}{9}\) smaller than 1,729.
Question 12.
Construct Arguments Carl and Maeve are asked to think of a fraction and multiply it by 5,267. Carl thinks of \(\frac{5}{6}\). Maeve thinks of \(\frac{7}{7}\). They both say their product is less than 5,267. Are they correct? Explain.
Answer:
Yes, they are correct.
Explanation:
Given that Carl thinks of \(\frac{5}{6}\) and Maeve thinks of \(\frac{7}{7}\). So Carl is correct and Maeve is same.
I’m in a Learning Mindset!
What helps me go from one learning activity to a different one?