We included HMH Into Math Grade 5 Answer Key PDF Module 8 Lesson 7 Multiply Fractions to make students experts in learning maths.
HMH Into Math Grade 5 Module 8 Lesson 7 Answer Key Multiply Fractions
I Can solve problems involving the multiplication of a whole number or fraction by a fraction.
Step it Out
1. An annual fundraiser raised \(\frac{4}{5}\) of the amount of money in 2017 as it did in 2018. Five-thousand dollars was raised in 2018. How much money was raised in 2017?
A. In which year do you think more money was raised? Explain your reasoning.

Answer:
In the year 2018, more money was raised.
B. Write an equation to model the problem. Write the whole number factor as a fraction.
Answer:
The equation is \(\frac{4}{5}\) × 5,000 = 4,000.
Explanation:
The equation to the problem is \(\frac{4}{5}\) × 5,000 which is 4 × 1,000 = 4,000.
C. Solve the equation 4 × 5,000 ÷ 5 = r. How does this equation compare to your equation from Part B?
Answer:
r = 4,000.
Explanation:
The equation is 4 × 5,000 ÷ 5 = r. Where r is 4,000.
D. How much money was raised in 2017? Write your answer as a whole number. How does your answer compare to your answer from Part A?
Answer:
The money raised in 2017 was less. As the money raised was 4,000.
2. A soccer team is having a fundraiser. Of the items they are selling, \(\frac{3}{4}\) are gift cards. Two-thirds of the gift cards are restaurant gift cards.

A. What fraction of the items they are selling are restaurant gift cards? Write an equation to model the problem.
_____________________
Answer:
\(\frac{1}{2}\).
Explanation:
The equation will be \(\frac{2}{3}\) × \(\frac{3}{4}\) which is \(\frac{1}{2}\).
B. Describe how you could have used a visual model to find the answer.
_____________________
Turn and Talk How do you know your answer is reasonable?
Check Understanding Math Board
Question 1.
Of the movies in Mr. Jackson’s collection, \(\frac{7}{10}\) are on DVD. Of those,
\(\frac{1}{2}\) are science fiction movies. What fraction of Mr. Jackson’s movies are science fiction DVDs?
Answer:
The fraction of Mr. Jackson’s movies are science fiction DVDs is \(\frac{7}{20}\).
Explanation:
Given that Mr. Jackson’s collection, \(\frac{7}{10}\) are on DVD and \(\frac{7}{10}\) is on DVD. So the fraction of Mr. Jackson’s movies are science fiction DVDs is \(\frac{7}{10}\) × \(\frac{1}{2}\) which is \(\frac{7}{20}\).
Find the product.
Question 2.
\(\frac{3}{8}\) × 16
Answer:
\(\frac{3}{8}\) × 16 = 6.
Explanation:
Given that the equation is \(\frac{3}{8}\) × 16 which is 3× 2 = 6.
Question 3.
\(\frac{1}{2}\) × \(\frac{3}{5}\)
Answer:
\(\frac{1}{2}\) × \(\frac{3}{5}\) = \(\frac{3}{10}\).
Explanation:
Given that the equation is \(\frac{1}{2}\) × \(\frac{3}{5}\) which is \(\frac{3}{10}\).
Question 4.
\(\frac{1}{3}\) × 4
Answer:
\(\frac{1}{3}\) × 4 = 1\(\frac{1}{3}\).
Explanation:
Given that the equation is \(\frac{1}{3}\) × 4 which is \(\frac{4}{3}\) = 1\(\frac{1}{3}\).
On Your Own
Question 5.
Use Structure Does the order of the factors change the product? Explain.
18 × \(\frac{3}{8}\) = ![]() \(\frac{3}{8}\) × 18 =
\(\frac{3}{8}\) × 18 = ![]()
Answer:
No
Explanation:
Given the equations are 18 × \(\frac{3}{8}\) which is \(\frac{54}{8}\) and \(\frac{3}{8}\) × 18 which is \(\frac{54}{8}\). Here, we can see that the product doesn’t change. As multiplication is commutative, so changing the order of the product of the factors will not be changed.
Find the product.
Question 6.
\(\frac{5}{9}\) × 18
Answer:
\(\frac{5}{9}\) × 18 = 10.
Explanation:
Given the equation is \(\frac{5}{9}\) × 18 which is 10.
Question 7.
32 × \(\frac{2}{3}\)
Answer:
32 × \(\frac{2}{3}\) = 21\(\frac{1}{3}\).
Explanation:
Given the equation is 32 × \(\frac{2}{3}\) which is \(\frac{64}{3}\) = 21\(\frac{1}{3}\).
Question 8.
\(\frac{7}{8}\) × \(\frac{9}{10}\)
Answer:
\(\frac{7}{8}\) × \(\frac{9}{10}\) = \(\frac{63}{80}\).
Explanation:
Given the equation is \(\frac{7}{8}\) × \(\frac{9}{10}\) which is \(\frac{63}{80}\).
Question 9.
Evaluate the numerical expression. \(\frac{5}{6}\) × (16 – 4)
- Which operation do you perform first? ____
- Write this answer as a fraction. _____
- What is the product of the numerators? _____
- What is the product of the denominators? ____
- What is the value of the numerical expression? ____
Answer:
\(\frac{5}{6}\) × (16 – 4) = 10.
Explanation:
Here, we perform bracket first which is 16 – 4 = 12.
This answer as a fraction is \(\frac{12}{1}\).
The product of the numerators is 5×12 = 60.
The product of the denominators is 6×1 = 6.
The value of the numerical expression is \(\frac{60}{6}\) = 10.
Question 10.
Explain how to find \(\frac{11}{12}\) of 4 by evaluating the numerical expression 11 × 4 ÷ 12.
Answer:
11 × 4 ÷ 12 = 3\(\frac{8}{12}\).
Explanation:
Given the expression is 11 × 4 ÷ 12, first we will multiply 11 × 4 which is 44 and then we will divide it by 12 which is 44÷12 which is 3\(\frac{8}{12}\).
Question 11.
Reason Sam is using craft felt to carpet two rooms in a dollhouse. Both rooms are \(\frac{5}{6}\) feet by \(\frac{7}{8}\) feet. How many square feet of craft felt does Sam need to carpet both rooms? Explain your reasoning.
Answer:
1\(\frac{22}{48}\) sqft.
Explanation:
Given that Both rooms are \(\frac{5}{6}\) feet by \(\frac{7}{8}\) feet. So the square feet of craft felt does Sam need to carpet both rooms is \(\frac{5}{6}\) × \(\frac{7}{8}\) which is \(\frac{35}{48}\). As for two rooms we will multiply with 2, so \(\frac{35}{48}\) × 2 which is 1\(\frac{22}{48}\) sqft.
Question 12.
Model with Mathematics The British Telecom Tower is about \(\frac{3}{7}\) the height of the Empire State Building. Write two different numerical expressions to model the height of the British Telecom Tower.
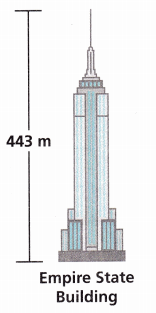
Answer:
The two expressions are \(\frac{3}{7}\)×443 and (3×443) ÷ 7.
Explanation:
Given that the British Telecom Tower is about \(\frac{3}{7}\) the height of the Empire State Building. So two different numerical expressions to model the height of the British Telecom Tower is \(\frac{3}{7}\)×443 and (3×443) ÷ 7.
Question 13.
Use Structure Kasim picks 8 pounds of strawberries. He uses \(\frac{5}{8}\) of the strawberries to make a fruit salad. Then he uses \(\frac{2}{3}\) of the remaining strawberries to make fruit smoothies. How many pounds of strawberries does Kasim have left after making fruit salad and smoothies? _______
Answer:
The number of pounds is 2.
Explanation:
Given that Kasim picks 8 pounds of strawberries and he uses \(\frac{5}{8}\) of the strawberries to make a fruit salad which is \(\frac{5}{8}\) × 8 = 5. Then he uses \(\frac{2}{3}\) of the remaining strawberries to make fruit smoothies which is \(\frac{2}{3}\) × 3 which is 2.
Find the product.
Question 14.
\(\frac{3}{5}\) × 7 = ____
Answer:
\(\frac{3}{5}\) × 7 = 4\(\frac{1}{5}\).
Explanation:
Given the equation is \(\frac{3}{5}\) × 7 which is \(\frac{21}{5}\) = 4\(\frac{1}{5}\).
Question 15.
\(\frac{1}{8}\) × \(\frac{2}{3}\) = ____
Answer:
\(\frac{1}{8}\) × \(\frac{2}{3}\) = \(\frac{1}{12}\).
Explanation:
Given the equation is \(\frac{1}{8}\) × \(\frac{2}{3}\) which is \(\frac{1}{12}\).
Question 16.
\(\frac{9}{11}\) ÷ (5 × 3) = ___
Answer:
\(\frac{9}{11}\) ÷ (5 × 3) = 12\(\frac{3}{11}\).
Explanation:
Given the equation is \(\frac{9}{11}\) ÷ (5 × 3). First we will solve the bracket which is 5 × 3 = 15 and \(\frac{9}{11}\) ÷ 15 which is \(\frac{135}{11}\) = 12\(\frac{3}{11}\).
Question 17.
\(\frac{17}{20}\) × (12 ÷ 2) = ___
Answer:
\(\frac{17}{20}\) × (12 ÷ 2) = 5\(\frac{1}{5}\).
Explanation:
Given the equation is \(\frac{17}{20}\) × (12 ÷ 2). First we will solve the bracket which is 12 ÷ 2 = 6 and \(\frac{17}{20}\) × 6 which is \(\frac{102}{20}\) = 5\(\frac{1}{5}\).
Question 18.
Reason Will the product be greater than, less than, or equal to 34? Explain your reasoning.
\(\frac{1}{3}\) × \(\frac{1}{3}\) × \(\frac{1}{3}\) × 34
Answer:
\(\frac{34}{27}\) which is less than 34.
Explanation:
Given the equation is \(\frac{1}{3}\) × \(\frac{1}{3}\) × \(\frac{1}{3}\) × 34 which is \(\frac{34}{27}\) which is less than 34.
Question 19.
Construct Arguments Jorge models the area of the rectangle with the equation \(\frac{2}{3}\) × 3 = m. Caleb models the area of the rectangle with the equation 2 × 3 ÷ 3 = p. Which equation is correct? Explain your reasoning.
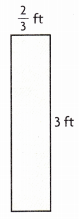
Answer:
They both are correct.
Explanation:
Given that the equation Joorge is \(\frac{2}{3}\) × 3 = m where m is 2 sq ft and Caleb models the area of the rectangle with the equation (2 × 3) ÷ 3 = p where p is 6 ÷ 3 = p, p = 2 sq ft. So they both are correct.