We included HMH Into Math Grade 5 Answer Key PDF Module 8 Lesson 5 Use Representations of Area to Develop Procedures to make students experts in learning maths.
HMH Into Math Grade 5 Module 8 Lesson 5 Answer Key Use Representations of Area to Develop Procedures
I Can find the product of fractions using an area model.
Spark Your Learning
A contractor buys rectangular floor tiles for a home that he is building. How can you find the area of
the tile?

Answer:
\(\frac{1}{4}\) ft.
Explanation:
The area of the given rectangle is \(\frac{1}{3}\) × \(\frac{3}{4}\) which is \(\frac{1}{4}\) ft
Use the square to help you find the area of the tile. Explain your reasoning.
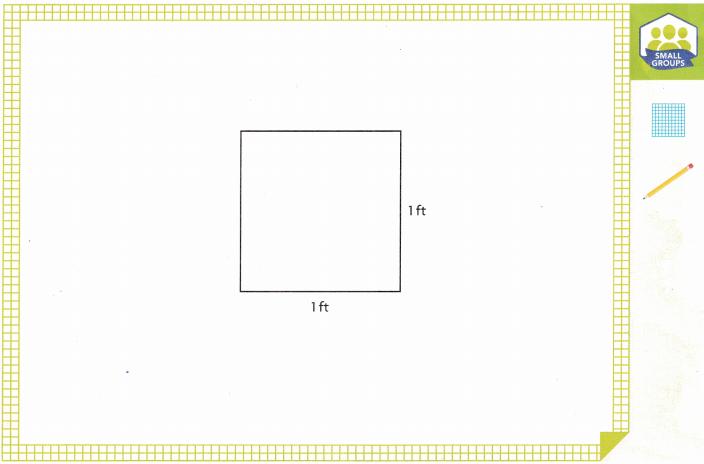
Answer:
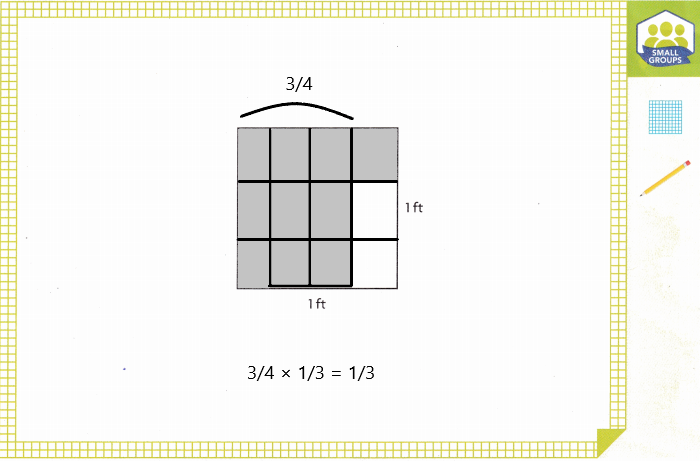
Turn and Talk Why was a square used to make the visual model?
Build Understanding
1. To tile a different room, the tile shown at the right is used.

Answer:
\(\frac{1}{2}\) sqft.
Explanation:
The area of the tile is \(\frac{2}{3}\) × \(\frac{3}{4}\) which is \(\frac{1}{2}\) sqft.
Use the square to help you find the area of the tile.
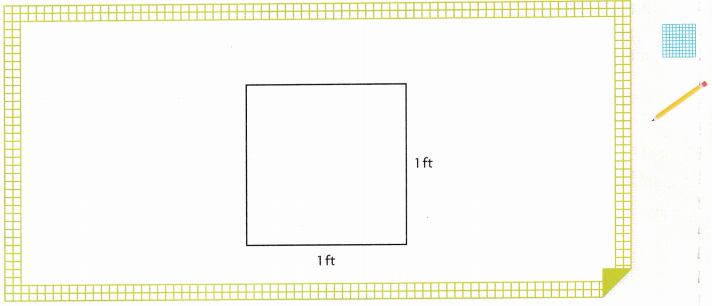
Answer:
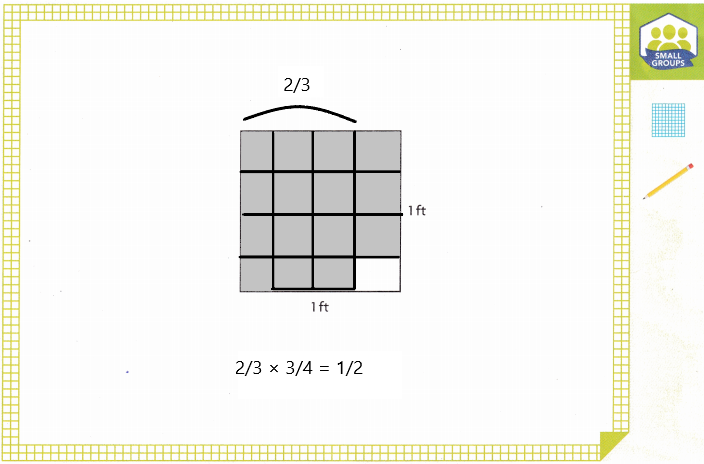
A. How can you use your area model to find the area of the tile?
__________________________
__________________________
B. What is the area of the tile? Write a multiplication equation to model the problem.
Answer:
\(\frac{1}{2}\) sqft.
Explanation:
The multiplication equation of the problem is \(\frac{2}{3}\) × \(\frac{3}{4}\) which is \(\frac{1}{2}\) sqft.
Turn and Talk What do you notice when you compare the numerator and the denominator of the product with the numerators and denominators in the factors?
Answer:
In the numerator, the fraction shows the number of parts we have out of the whole. And the denominator shows how many equal parts there are in total.
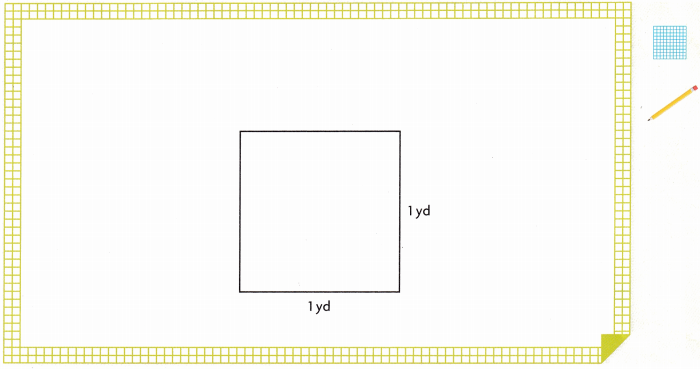
2. For another room in the house that he is building, the contractor uses floorboards with the dimensions shown.

Answer:
he area of the floorboard is \(\frac{1}{3}\) sq yd.
Explanation:
Given that the sides of the floorboard are \(\frac{3}{4}\) and \(\frac{4}{9}\) and the area of the floorboard is \(\frac{3}{4}\) × \(\frac{4}{9}\) which is \(\frac{1}{3}\) sq yd.
Draw an area model to find the area of a floorboard.
Answer:
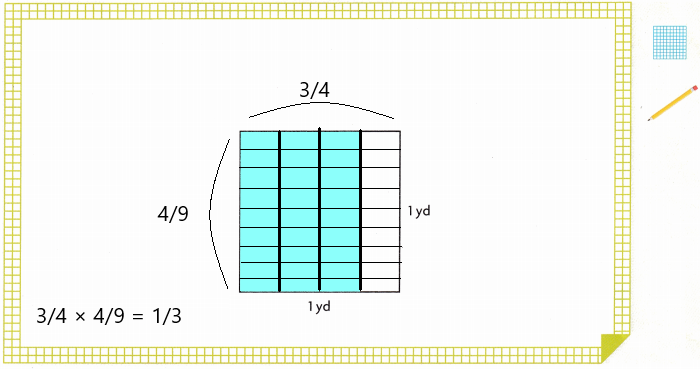
A. What is the area of the floorboard? _______
Answer:
The area of the floorboard is \(\frac{1}{3}\) sq yd.
B. The area of the floorboard can be modeled with the equation shown. Multiply the numerators. Then multiply the denominators. Write your answers in the boxes.
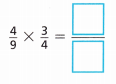
Answer:
\(\frac{1}{3}\).
Explanation:
By multiplying numerators and denominators \(\frac{4}{9}\) × \(\frac{3}{4}\) which is \(\frac{1}{3}\).
C. Compare your answers from Parts A and B.
______________________
Answer:
By comparing part A and part B \(\frac{1}{3}\) = \(\frac{1}{3}\) they both are equal.
D. How can you find the product of two fractions without using a visual model? Explain your thinking.
______________________
______________________
______________________
Step It Out
3. A store is selling new wooden floorboards that measure \(\frac{2}{3}\) yard by \(\frac{1}{12}\) yard.

Answer:
\(\frac{1}{18}\) sq yd.
Explanation:
Given that a store is selling new wooden floorboards that measure \(\frac{2}{3}\) yard by \(\frac{1}{12}\) yard. So the area of the new wooden floorboard is \(\frac{2}{3}\) × \(\frac{1}{12}\) which is \(\frac{1}{18}\) sq yd.
A. What is the area of the floorboard? Write a multiplication equation to model the problem.
Answer:
The area of the floorboard is \(\frac{1}{18}\) sq yd.
Explanation:
The multiplication equation is \(\frac{2}{3}\) × \(\frac{1}{12}\) which is \(\frac{1}{18}\) sq yd.
B. Describe how you could use an area model to check your answer from Part A.
Turn and Talk How would your answer in Part A change if you reversed the order of the factors in the equation? Explain.
Check Understanding Math Board
Question 1.
Mrs. Lin is using tiles that measure \(\frac{1}{2}\) foot by \(\frac{2}{3}\) foot. What is the area of each tile? Write a multiplication equation to model the problem.
Answer:
The area of each tile is \(\frac{1}{3}\) sq ft.
Explanation:
Given that Mrs. Lin is using tiles that measure \(\frac{1}{2}\) foot by \(\frac{2}{3}\) foot. So the area of the tiles is \(\frac{1}{2}\) × \(\frac{2}{3}\) which is \(\frac{1}{3}\) sq ft.
Question 2.
To fit in a corner, a contractor cuts the tile shown in half. What is the area of one piece of the cut tile? Write a multiplication equation to model the area. Find the product.
Answer:
The area is \(\frac{1}{3}\) sq ft.
Explanation:
The area of one piece of the cut tile is \(\frac{1}{2}\) × \(\frac{2}{3}\) which is \(\frac{1}{3}\) sq ft.
Question 3.
\(\frac{3}{8}\) × \(\frac{2}{3}\)
Answer:
\(\frac{3}{8}\) × \(\frac{2}{3}\) = \(\frac{1}{4}\).
Explanation:
By multiplying \(\frac{3}{8}\) × \(\frac{2}{3}\) we will get \(\frac{1}{4}\).
Question 4.
\(\frac{4}{9}\) × \(\frac{3}{5}\)
Answer:
\(\frac{4}{9}\) × \(\frac{3}{5}\) = \(\frac{4}{15}\).
Explanation:
By multiplying \(\frac{4}{9}\) × \(\frac{3}{5}\) we will get \(\frac{4}{15}\).
Question 5.
\(\frac{3}{2}\) × \(\frac{9}{12}\)
Answer:
\(\frac{3}{2}\) × \(\frac{9}{12}\) = 1\(\frac{1}{8}\).
Explanation:
By multiplying \(\frac{3}{2}\) × \(\frac{9}{12}\) we will get 1\(\frac{1}{8}\).
On Your Own
Question 6.
Attend to Precision A farm field measures \(\frac{3}{8}\) mile wide by \(\frac{2}{3}\) mile long. What fraction of a square mile is the area of the field? Explain how you found your answer.
Answer:
The fraction of a square mile is the area of the field that is \(\frac{1}{4}\).
Explanation:
Given that a farm field measures \(\frac{3}{8}\) mile wide by \(\frac{2}{3}\) mile long. So the fraction of a square mile is the area of the field that is \(\frac{3}{8}\) × \(\frac{2}{3}\) which is \(\frac{1}{4}\).
Question 7.
Use Tools Mr. Chiu has a large box for wet boots in his classroom. He wants to put plastic sheeting under the box. The dimensions of the bottom are \(\frac{3}{4}\) yard and \(\frac{7}{8}\) yard. How much sheeting does he need?
- Use the square to find the area of the bottom of the box.
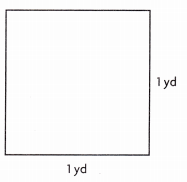
- How many small rectangles represent the area of the bottom of the box? What area does each small rectangle drawn in your model represent?
_____________________ - How much sheeting does he need? Write an equation to model the problem.
_____________________
Answer:
\(\frac{21}{32}\).
Explanation:
Given that the dimensions of the bottom are \(\frac{3}{4}\) yard and \(\frac{7}{8}\) yard. So the sheet needed is \(\frac{3}{4}\) × \(\frac{7}{8}\) which is \(\frac{21}{32}\).
Find the product.
Question 8.
\(\frac{5}{6}\) × \(\frac{2}{5}\)
Answer:
\(\frac{5}{6}\) × \(\frac{2}{5}\) = \(\frac{2}{5}\).
Explanation:
The multiplication of \(\frac{5}{6}\) × \(\frac{2}{5}\) is \(\frac{1}{3}\).
Question 9.
\(\frac{3}{8}\) × \(\frac{3}{7}\)
Answer:
\(\frac{3}{8}\) × \(\frac{3}{7}\) = \(\frac{9}{56}\).
Explanation:
The multiplication of \(\frac{3}{8}\) × \(\frac{3}{7}\) is \(\frac{9}{56}\).
Question 10.
\(\frac{3}{5}\) × \(\frac{5}{8}\)
Answer:
\(\frac{3}{5}\) × \(\frac{5}{8}\) = \(\frac{3}{8}\).
Explanation:
The multiplication of \(\frac{3}{5}\) × \(\frac{5}{8}\) is \(\frac{3}{8}\).
Question 11.
Use Structure Explain how you can find the product \(\frac{1}{2}\) × \(\frac{2}{3}\) × \(\frac{3}{4}\) using area models.
Answer:
The product is \(\frac{1}{4}\).
Explanation:
The product of \(\frac{1}{2}\) × \(\frac{2}{3}\) × \(\frac{3}{4}\) is \(\frac{1}{4}\).
Question 12.
Use Tools Use the square to find the area of the rectangle shown.
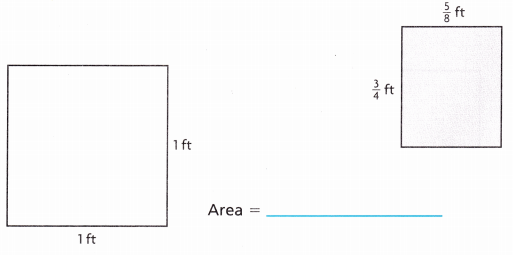
Answer:
Area is \(\frac{15}{32}\).
Explanation:
The area is \(\frac{5}{8}\) × \(\frac{3}{4}\) which is \(\frac{15}{32}\)
Question 13.
A sheet of paper measures \(\frac{7}{12}\) foot by \(\frac{7}{8}\) foot. What is the area of the sheet of paper?
Answer:
Area is \(\frac{49}{96}\) sq ft.
Explanation:
Given that a sheet of paper measures \(\frac{7}{12}\) foot by \(\frac{7}{8}\) foot. So the area of the sheet of paper is \(\frac{7}{12}\) × \(\frac{7}{8}\) which is \(\frac{49}{96}\) sq ft.
I’m in a Learning Mindset!
How did I use feedback my teacher gave me?
___________________________
___________________________