We included HMH Into Math Grade 5 Answer Key PDF Module 6 Lesson 4 Rewrite Fractions with a Common Denominator to make students experts in learning maths.
HMH Into Math Grade 5 Module 6 Lesson 4 Answer Key Rewrite Fractions with a Common Denominator
I Can generate equivalent fractions for given fractions using a common denominator.
Spark Your Learning
TV show hosts Ben and Isa are preparing small pieces of French toast from slices of bread. Ben cuts his slice into two equal sections. Isa cuts her slice into three equal sections. All of the sections were supposed to be cut into the same-sized pieces.

Draw a visual model to show what Ben and Isa should do to correct the sizes of their sections of French toast.

Answer:
\(\frac{1}{2}\), \(\frac{1}{3}\)
LCD is 6.
\(\frac{1}{2}\) × \(\frac{3}{3}\), \(\frac{1}{3}\) × \(\frac{2}{2}\)
\(\frac{3}{6}\), \(\frac{2}{6}\)
Turn and Talk What if Ben had cut his slice into fourths instead of halves? What would Ben and Isa need to do then?
Build Understanding
1. The circle represents all the people who watch The Morning Show. What equivalent fractions can you write to represent the different ways people watch The Morning Show?
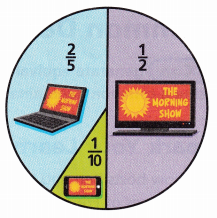
A. List nonzero multiples of 2, 5, and 10.
2: ________
5: _________
10: ______
B. What is a common multiple of 2, 5, and 10?
________________
C. Use the common multiple you found to write equivalent fractions.
\(\frac{1}{2}\) = ____ \(\frac{2}{5}\) = ___ \(\frac{1}{10}\) = ____
Connect to Vocabulary
Fractions that name the same amount or part are equivalent fractions. For example, and are equivalent fractions.
D. How can a common multiple and equivalent fractions help you add and subtract fractions?
E. Write a numerical expression using equivalent fractions that models all the people who watch The Morning Show.
______________
Answer:
Multiples of 2 – 2, 4, 6, 8, 10
Multiples of 5 – 5, 10
Multiples of 10 – 10
The LCM of 2, 5, and 10 is 10.
\(\frac{1}{2}\) = \(\frac{5}{10}\)
\(\frac{2}{5}\) = \(\frac{4}{10}\)
\(\frac{1}{10}\) = \(\frac{1}{10}\)
By using the common denominator we can add or subtract the fractions.
Turn and Talk How do you know how many multiples to list when you are finding a common multiple of 2, 5, and 10?
Answer:
Multiples of 2 – 2, 4, 6, 8, 10
Multiples of 5 – 5, 10
Multiples of 10 – 10
The LCM of 2, 5, and 10 is 10.
Step It Out
2. Trina makes decorations using wire. She has one piece of wire that is \(\frac{1}{6}\) foot and another piece that is \(\frac{3}{4}\) foot. What equivalent fractions represent the amounts of wire that Trina has?

A. Find the product of the denominators of each fraction. How is your answer related to the common multiples of 4 and 6?
B. What equivalent fractions with a common denominator can you write for \(\frac{3}{4}\) and \(\frac{1}{6}\)?
C. What numerical expression using equivalent fractions models the amount of wire that Trina has?
Answer:
Given,
Trina makes decorations using wire. She has one piece of wire that is \(\frac{1}{6}\) foot and another piece that is \(\frac{3}{4}\) foot.
The common multiple of 4 and 6 is 12.
\(\frac{1}{6}\) × \(\frac{2}{2}\), \(\frac{3}{4}\) × \(\frac{3}{3}\)
So, the equivalent fractions are \(\frac{2}{12}\), \(\frac{9}{12}\)
Connect to Vocabulary
A common denominator is a common multiple of two or more denominators. Any two or more fractions can be expressed as equivalent fractions with a common denominator.
Check Understanding Math Board
Question 1.
Aya, Kate, and un bring all the food to a picnic. Aya brings \(\frac{3}{4}\), Kate brings \(\frac{1}{6}\), and Jin brings \(\frac{1}{12}\). Write a numerical expression
using equivalent fractions with a common denominator to model the amounts of food they bring to the picnic.
______________________
Answer:
Given,
Aya, Kate, and un bring all the food to a picnic. Aya brings \(\frac{3}{4}\), Kate brings \(\frac{1}{6}\), and Jin brings \(\frac{1}{12}\).
\(\frac{3}{4}\), \(\frac{1}{12}\)
The denominators of both the fractions are not the same. So we have to find the least common denominator of the given fractions.
Common denominator is 24
\(\frac{3}{4}\) × \(\frac{6}{6}\), \(\frac{1}{12}\) × \(\frac{2}{2}\)
So, the equivalent fractions are \(\frac{18}{24}\), \(\frac{2}{24}\)
Find a common denominator. Then use the common denominator to write equivalent fractions.
Question 2.
\(\frac{3}{4}\), \(\frac{1}{8}\)
Common denominator: ______
Answer: 8
Explanation:
\(\frac{3}{4}\), \(\frac{1}{8}\)
The denominators of both the fractions are not the same. So we have to find the least common denominator of the given fractions.
LCD is 8.
\(\frac{6}{8}\), \(\frac{1}{8}\)
Question 3.
\(\frac{1}{4}\), \(\frac{5}{6}\)
Common denominator: ______
Answer: Common denominator: 12
Explanation:
\(\frac{1}{4}\), \(\frac{5}{6}\)
The denominators of both the fractions are not the same. So we have to find the least common denominator of the given fractions.
Common denominator of 4 and 6 is 12.
\(\frac{1}{4}\) × \(\frac{3}{3}\), \(\frac{5}{6}\) × \(\frac{2}{2}\)
So, the equivalent fractions are \(\frac{3}{12}\), \(\frac{10}{12}\)
On Your Own
Question 4.
Reason The Morning Show has a \(\frac{1}{5}\)-hour weather section and a \(\frac{1}{2}\)-hour news section. How can you determine the amount of time spent on weather and news without using drawings?

Answer:
Given,
The Morning Show has a \(\frac{1}{5}\)-hour weather section and a \(\frac{1}{2}\)-hour news section.
\(\frac{1}{5}\), \(\frac{1}{2}\)
The denominators of both the fractions are not the same. So we have to find the least common denominator of the given fractions.
Common denominator is 10.
\(\frac{1}{5}\) × \(\frac{2}{2}\), \(\frac{1}{2}\) × \(\frac{5}{5}\)
\(\frac{2}{10}\), \(\frac{5}{10}\)
So, the amount of time spent on weather and news are \(\frac{2}{10}\), \(\frac{5}{10}\)
Use a common denominator to write equivalent fractions.
Question 5.
\(\frac{1}{2}\), \(\frac{5}{12}\)
Answer:
\(\frac{1}{2}\), \(\frac{5}{12}\)
The denominators of both the fractions are not the same. So we have to find the least common denominator of the given fractions.
Common denominator is 12
\(\frac{6}{12}\), \(\frac{5}{12}\)
The equivalent fractions of the given fractions are
\(\frac{6}{12}\) × \(\frac{2}{2}\), \(\frac{5}{12}\) × \(\frac{2}{2}\)
So, the equivalent fractions are \(\frac{12}{24}\), \(\frac{10}{24}\)
Question 6.
\(\frac{2}{3}\), \(\frac{1}{6}\)
Answer:
\(\frac{2}{3}\), \(\frac{1}{6}\)
The denominators of both the fractions are not the same. So we have to find the least common denominator of the given fractions.
LCD is 6.
\(\frac{2}{3}\) × \(\frac{2}{2}\), \(\frac{1}{6}\)
\(\frac{4}{6}\), \(\frac{1}{6}\)
The equivalent fractions of the given fractions are
\(\frac{4}{6}\) × \(\frac{2}{2}\), \(\frac{1}{6}\) × \(\frac{2}{2}\)
So, the equivalent fractions are \(\frac{8}{12}\), \(\frac{2}{12}\)
Question 7.
\(\frac{2}{3}\), \(\frac{3}{8}\)
Answer:
\(\frac{2}{3}\), \(\frac{3}{8}\)
The denominators of both the fractions are not the same. So we have to find the least common denominator of the given fractions.
\(\frac{2}{3}\) × \(\frac{8}{8}\), \(\frac{3}{8}\) × \(\frac{3}{3}\)
\(\frac{16}{24}\), \(\frac{9}{24}\)
So, the equivalent fractions are \(\frac{16}{24}\), \(\frac{9}{24}\)
Question 8.
\(\frac{1}{4}\), \(\frac{3}{5}\)
Answer:
\(\frac{1}{4}\), \(\frac{3}{5}\)
The denominators of both the fractions are not the same. So we have to find the least common denominator of the given fractions.
LCD is 20.
\(\frac{1}{4}\) × \(\frac{5}{5}\), \(\frac{3}{5}\) × \(\frac{4}{4}\)
\(\frac{5}{20}\), \(\frac{12}{20}\)
So, the equivalent fractions are \(\frac{5}{20}\), \(\frac{12}{20}\)
Question 9.
\(\frac{3}{4}\), \(\frac{1}{6}\)
Answer:
\(\frac{3}{4}\), \(\frac{1}{6}\)
The denominators of both the fractions are not the same. So we have to find the least common denominator of the given fractions.
Common denominator of 4 and 6 is 12.
\(\frac{3}{4}\) × \(\frac{3}{3}\), \(\frac{1}{6}\) × \(\frac{2}{2}\)
\(\frac{9}{12}\), \(\frac{2}{12}\)
So, the equivalent fractions are \(\frac{9}{12}\), \(\frac{2}{12}\)
Question 10.
\(\frac{2}{3}\), \(\frac{3}{5}\)
Answer:
\(\frac{2}{3}\), \(\frac{3}{5}\)
The denominators of both the fractions are not the same. So we have to find the least common denominator of the given fractions.
LCD is 15.
\(\frac{2}{3}\) × \(\frac{5}{5}\), \(\frac{3}{5}\) × \(\frac{3}{3}\)
\(\frac{10}{15}\), \(\frac{9}{15}\)
So, the equivalent fractions are \(\frac{10}{15}\), \(\frac{9}{15}\)
Question 11.
STEM Temperature is one factor that determines the weather. In Tavernier, Florida, the average monthly high temperature (°F) is in the 70s for \(\frac{1}{3}\) of the year, in the 80s for \(\frac{1}{2}\) of the year, and in the 90s for \(\frac{1}{6}\) of the year. Write a numerical expression using equivalent fractions with a common denominator to model the part of the year with these average temperatures.
Answer:
Given,
Temperature is one factor that determines the weather. In Tavernier, Florida, the average monthly high temperature (°F) is in the 70s for \(\frac{1}{3}\) of the year, in the 80s for \(\frac{1}{2}\) of the year, and in the 90s for \(\frac{1}{6}\) of the year.
\(\frac{1}{3}\), \(\frac{1}{2}\), \(\frac{1}{6}\)
The least common denominator of 2, 3, and 6 is 6.
\(\frac{1}{3}\) × \(\frac{2}{2}\), \(\frac{1}{2}\) × \(\frac{3}{3}\), \(\frac{1}{6}\) × \(\frac{1}{1}\)
\(\frac{2}{6}\), \(\frac{3}{6}\), \(\frac{1}{6}\)
I’m in a Learning Mindset!
How do I break down finding a common denominator into smaller steps?
__________________________
Answer:
- List the multiples for each number.
- Look at the lists you’ve made. Underline any numbers that appear on both lists.
- Look for the least common multiple or LCM. This. is your common denominator.
- Multiply the numerator and denominator of each fraction by the factor that it.