We included HMH Into Math Grade 5 Answer Key PDF Module 6 Lesson 2 Represent Addition with Different-Sized Parts to make students experts in learning maths.
HMH Into Math Grade 5 Module 6 Lesson 2 Answer Key Represent Addition with Different-Sized Parts
I Can represent the sum of fractions with different-sized parts using a visual model.
Spark Your Learning
Julia runs through an obstacle course. She climbs a cargo net in \(\frac{1}{4}\) minute. Then she crosses the balance beam in \(\frac{1}{6}\) minute. How long does Julia take to complete both obstacles?

Draw to show your reasoning.

How long does Julia take to complete both obstacles?
Answer:
Given,
Julia runs through an obstacle course. She climbs a cargo net in \(\frac{1}{4}\) minute. Then she crosses the balance beam in \(\frac{1}{6}\) minute.
\(\frac{1}{4}\) + \(\frac{1}{6}\)
LCD is 12.
\(\frac{2}{12}\) + \(\frac{3}{12}\) = \(\frac{5}{12}\) minute
Thus Julia takes \(\frac{5}{12}\) minute to complete both obstacles.
Turn and Talk As her final obstacle, Julia finishes the army crawl in \(\frac{1}{2}\) minute. Does she finish the three obstacles in less than 1 minute? Explain.
Build Understanding
1. Some obstacle courses include a rope climb. On his first try, Travis climbs \(\frac{2}{3}\) of the length of the rope. On his second try, he climbs more than his first try by \(\frac{1}{6}\) of the length of rope. What part of the rope does Travis climb on his second try?

Complete the fraction model to solve the problem. Draw to show your thinking.
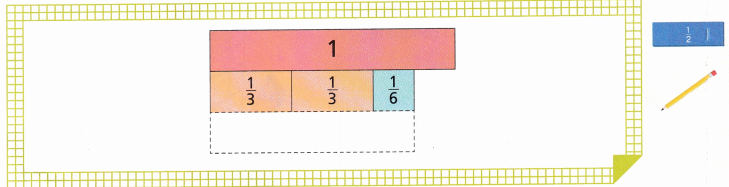
A. One student used all \(\frac{1}{6}\)-fraction strips to find the part of the rope Travis climbed on his second try. Another student used \(\frac{1}{12}\)-fraction strips. Who is correct and how do you know?
B. Could you use only thirds to represent the sum? Explain.
________________________
________________________
C. Write an equation to model your solution. ________________________
D. What part of the rope does Travis climb on his second try?
________________________
Answer:
Given,
On his first try, Travis climbs \(\frac{2}{3}\) of the length of the rope.
On his second try, he climbs more than his first try by \(\frac{1}{6}\) of the length of rope.
\(\frac{2}{3}\) + \(\frac{1}{6}\)
LCD is 6.
\(\frac{4}{6}\) + \(\frac{1}{6}\) = \(\frac{5}{6}\)
The student who used all \(\frac{1}{6}\)-fraction strips to find the part of the rope Travis climbed on his second try.
Travis Climb \(\frac{5}{6}\) part of the rope on his second try.
Turn and Talk A student solves this problem by looking at the fraction strip that was missing. What could this student have been thinking?
2. To make the obstacle course more challenging, the swinging rings are moved \(\frac{1}{2}\) foot farther apart. If they were \(\frac{5}{8}\) foot apart, how far apart are the rings now?

A. How does the new distance between the rings compare to the length of 1 foot?
B. Draw a visual model to represent the situation.
C. How far apart are the rings now? How do you know?
Answer:
Given that,
The foot apart is 5/8.
The swinging rings are moved 1/2 foot farther apart.
The total swinging rings moved are 5/8 + 1/2.
= (5 x 2) + (1 x 8)/8 x 2
= 10 + 8/16
= 18/16
= 9/8
Therefore the swinging ring’s move is 9/8.
The 9/8 is greater than the length of 1 foot.
Check Understanding Math Board
Question 1.
Jane buys a new pair of sneakers. The heel height of her old pair is \(\frac{5}{6}\) inch. The heel height of her new pair is \(\frac{1}{12}\) inch taller. What is the heel height of her new sneakers? Draw a visual model.
Answer:
Given that,
The heel height of her old pair is \(\frac{5}{6}\) = 5/6 inch.
The heel height of her new pair is \(\frac{1}{12}\) inch taller than the old pair.
The height of the new pair is 5/6 + 1/12
= (5 x 12) + (1 x 6)/6 x 12
= 60 + 6/72
= 66/72
= 11/12
Therefore the height of the new pair of heels is 11/12.
On Your Own
Question 2.
Use Structure Tina is making a vitamin drink to enjoy while training for an obstacle course. If she adds \(\frac{1}{2}\) cup of water to the mix, how many cups of vitamin drink does Tina make? Draw a visual model that supports your answer.

Answer:
Given that,
The full cup of vitamin drink is 3/4 cup.
Water added to the vitamin drink is 1/2 cup.
Therefore the total vitamin drink is 3/4 + 1/2
= (3 x 2) + (1 x 4)/4 x 2
= 6 + 4/8
= 10/8
= 5/4
The total vitamin drink is 5/4 or 1\(\frac{1}{4}\)
Use Tools Use a visual model to find the sum.
Question 3.
\(\frac{1}{4}\) + \(\frac{5}{6}\)
Answer:
\(\frac{1}{4}\) + \(\frac{5}{6}\)
LCD is 12.
\(\frac{3}{12}\) + \(\frac{10}{12}\) = \(\frac{13}{12}\)
Convert the improper fraction to the mixed fraction
\(\frac{13}{12}\) = 1 \(\frac{1}{12}\)
Question 4.
\(\frac{2}{3}\) + \(\frac{1}{6}\)
Answer:
Given that,
\(\frac{2}{3}\) + \(\frac{1}{6}\)
LCD is 6
\(\frac{4}{6}\) + \(\frac{1}{6}\) = \(\frac{5}{6}\)
Question 5.
\(\frac{3}{10}\) + \(\frac{1}{2}\)
Answer:
Given that,
\(\frac{3}{10}\) + \(\frac{1}{2}\)
LCD is 10
\(\frac{3}{10}\) + \(\frac{5}{10}\) = \(\frac{4}{5}\)
Question 6.
\(\frac{3}{5}\) + \(\frac{1}{2}\)
Answer:
\(\frac{3}{5}\) + \(\frac{1}{2}\)
LCD is 10.
\(\frac{6}{10}\) + \(\frac{5}{10}\) = \(\frac{11}{10}\)
Convert the improper fraction to the mixed fraction
\(\frac{11}{10}\) = 1 \(\frac{1}{10}\)
Question 7.
\(\frac{1}{12}\) + \(\frac{5}{6}\)
Answer:
Given that.
\(\frac{1}{12}\) + \(\frac{5}{6}\)
LCD is 12
\(\frac{1}{12}\) + \(\frac{10}{12}\) = \(\frac{11}{12}\).
Question 8.
\(\frac{3}{8}\) + \(\frac{3}{4}\)
Answer:
Given that,
\(\frac{3}{8}\) + \(\frac{3}{4}\)
LCD is 8
\(\frac{3}{8}\) + \(\frac{6}{6}\) = \(\frac{9}{8}\)
Convert the improper fraction to the mixed fraction
\(\frac{9}{8}\) = 1 \(\frac{1}{8}\)
Question 9.
Open Ended At the archery obstacle, Jasper’s arrow lands \(\frac{9}{10}\) inch from the center of the target. The distance from Jasper’s arrow to the center of the target is \(\frac{4}{5}\) inch less than the distance from Ali’s arrow to the center of the target. Write a question based on this situation and then answer it.
Answer:
Given,
At the archery obstacle, Jasper’s arrow lands \(\frac{9}{10}\) inch from the center of the target.
The distance from Jasper’s arrow to the center of the target is \(\frac{4}{5}\) inch less than the distance from Ali’s arrow to the center of the target.
Jasper’s arrow Landing distance = \(\frac{9}{10}\) inch
Ali’s arrow Landing distance = \(\frac{4}{5}\)
\(\frac{9}{10}\) + \(\frac{4}{5}\)
LCD is 10
\(\frac{9}{10}\) + \(\frac{8}{10}\) = \(\frac{17}{10}\)
Convert the improper fraction to the mixed fraction
\(\frac{17}{10}\) = 1\(\frac{7}{10}\)
I’m in a Learning Mindset!
How did collaborating with a partner support my learning about representing fractions with different-sized parts?